Kinetic Studies on ATRP
-
Determination of Reaction Parameters in an ATRP Reaction
-
Measurement of KATRP Equilibrium Constant and the Rate Constants for Activation and Deactivation
-
Determination of the Redox Potential of Copper Complexes
Determination of Reaction Parameters in an ATRP Reaction
Simply put, if you do not select the correct catalyst and correct conditions for ATRP, the reaction will not be controlled.
This section concentrates on the kinetic and thermodynamic parameters in the atom transfer equilibrium including, determination of the activation (kact) and deactivation (kdeact) rate constants and their dependence on the structure of the copperI complex. Additionally, the equilibrium constant, KEQ or KATRP = kact/kdeact, was determined via an analytical solution of the persistent radical effect.(1-3)
Kinetic studies
Knowledge of the dimension and impact of the kinetic parameters in a controlled/"living" radical polymerization (CRP) is of critical importance for the design of well-defined macromolecules. The rate of polymerization, molecular weight distribution and in case of copolymerization, the distribution of the comonomers along a given polymer segment are a direct consequence of kinetics. Therefore, understanding and measuring the kinetic parameters is a primary goal of the group.(4)
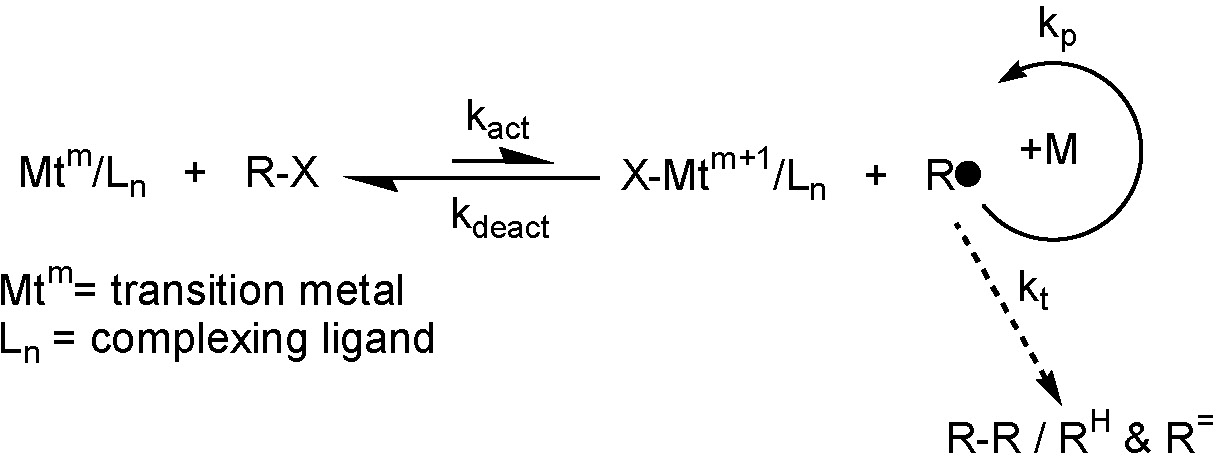
Mechanistically, ATRP is based on an inner sphere electron transfer process, which involves a reversible (pseudo)halogen transfer between a dormant species (R-X) and a transition metal complex (Mtm/Ln) resulting in the formation of propagating radicals (R*) and the metal complex in the higher oxidation state (e.g. X-Mtm+1/Ln). Radicals react reversibly with oxidized metal complexes, X-Mtn+1/Ligand, in a deactivation reaction to reform the dormant species and the transition metal complex (Mtm/Ln) in the lower oxidation state, i.e. the activator. These processes occur with a rate constant of activation, kact, and deactivation kdeact, respectively. Polymer chains grow by the addition of monomers to the periodically generated radicals in a manner similar to a conventional radical polymerization, with the rate constant of propagation, kp. Termination reactions (kt) also occur in ATRP, mainly through radical coupling and disproportionation. The rate of polymerization is ultimately governed by the position of the ATRP equilibrium, as illustrated in equation (1) for a particular monomer, M.
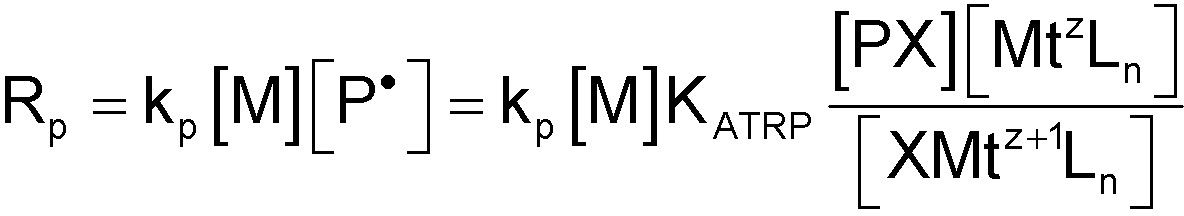
Quantifying KATRP for a given catalyst therefore provides an excellent measure of the catalyst's true activity in a polymerization reaction.(5) The ligand L dramatically affects the values of both rate constants, kact(6) and kdeact,(4) and therefore their ratio, KATRP.
The following equation illustrates how the polydispersity index of a polymer prepared by an ATRP, in the absence of chain termination and transfer, relates to the concentration of initiator (RX) and deactivator (D), the rate constants of propagation (kp) and deactivation (kdeact), and the monomer conversion (q).(7)
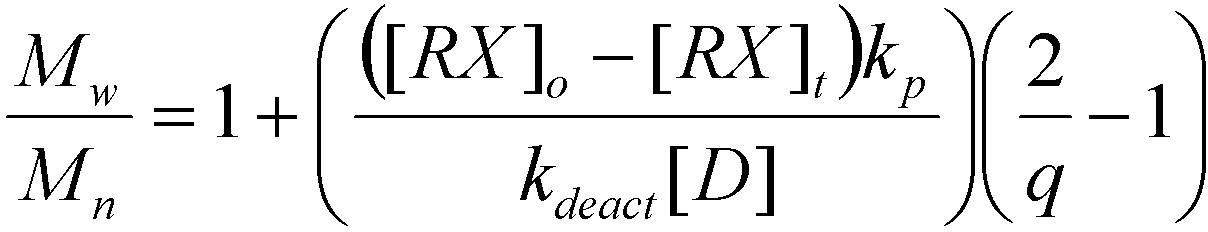
Thus, for the same monomer, a catalyst that deactivates the growing chains faster will produce polymers with a lower polydispersity index (smaller kp/kdeact). Alternatively, polydispersity index decreases with an increasing concentration of deactivator, although at the cost of slower rates of polymerization. For example, the addition of a small amount of CuII halides to the feedstock (5-10%) in a standard copper-based ATRP leads to better controlled polymerizations with decreased polymerization rates, as a consequence of instantaneous control and increased initiation efficiency due to increased rate of deactivation.(8,9)
This approach is particularly useful when conducting ATRP in aqueous / protic media. However the addition of Cu(II) to less polar media also affects the rate of activation, as does the ratio of added ligand to transition metal, and choice of solvent for a given catalyst complex.(10-12)
REFERENCES
(1) Shipp, D. A.; Matyjaszewski, K. Macromolecules 2000, 33, 1553-1559.
(2) Pintauer, T.; McKenzie, B.; Matyjaszewski, K. ACS Symposium Series 2003, 854, 130-147.
(3) Pintauer, T.; Braunecker, W.; Collange, E.; Poli, R.; Matyjaszewski, K. Macromolecules 2004, 37, 2679-2682.
(4) Tang, W.; Kwak, Y.; Braunecker, W.; Tsarevsky, N. V.; Coote, M. L.; Matyjaszewski, K. J. Am. Chem. Soc. 2008, 130, 10702-10713.
(5) Tang, W.; Tsarevsky, N. V.; Matyjaszewski, K. Journal of the American Chemical Society 2006, 128, 1598-1604.
(6) Tang, W.; Matyjaszewski, K. Macromolecules 2006, 39, 4953-4959.
(7) Matyjaszewski, K. Macromol. Symp. 1996, 111, 47-61.
(8) Matyjaszewski, K.; Wei, M.; Xia, J.; Gaynor, S. G. Macromol. Chem. Phys. 1998, 199, 2289-2292.
(9) Zhang, H.; Klumperman, B.; Ming, W.; Fischer, H.; van der Linde, R. Macromolecules 2001, 34, 6169-6173.
(10) Matyjaszewski, K.; Nanda, A. K.; Tang, W. Macromolecules 2005, 38, 2015-2018.
(11) Tang, W.; Nanda, A. K.; Matyjaszewski, K. Macromolecular Chemistry and Physics 2005, 206, 1171-1177.
(12) Tsarevsky, N. V.; Braunecker, W. A.; Brooks, S. J.; Matyjaszewski, K. Macromolecules 2006, 39, 6817-6824.
Measurement of KATRP Equilibrium Constant and the Rate Constants for Activation and Deactivation
Understanding, and controlling the equilibrium, and hence the dynamics of the atom transfer process, are basic prerequisites for running a successful ATRP. Therefore it is very important within the catalyst group to correlate structure with reactivity for each of the involved reagents, both oxidation states of the transition metal complex, radicals and dormant species, in addition to solvent effects and reaction temperature in order to provide that fundamental understanding required for the selection of optimum conditions to conduct the desired reaction.(1)
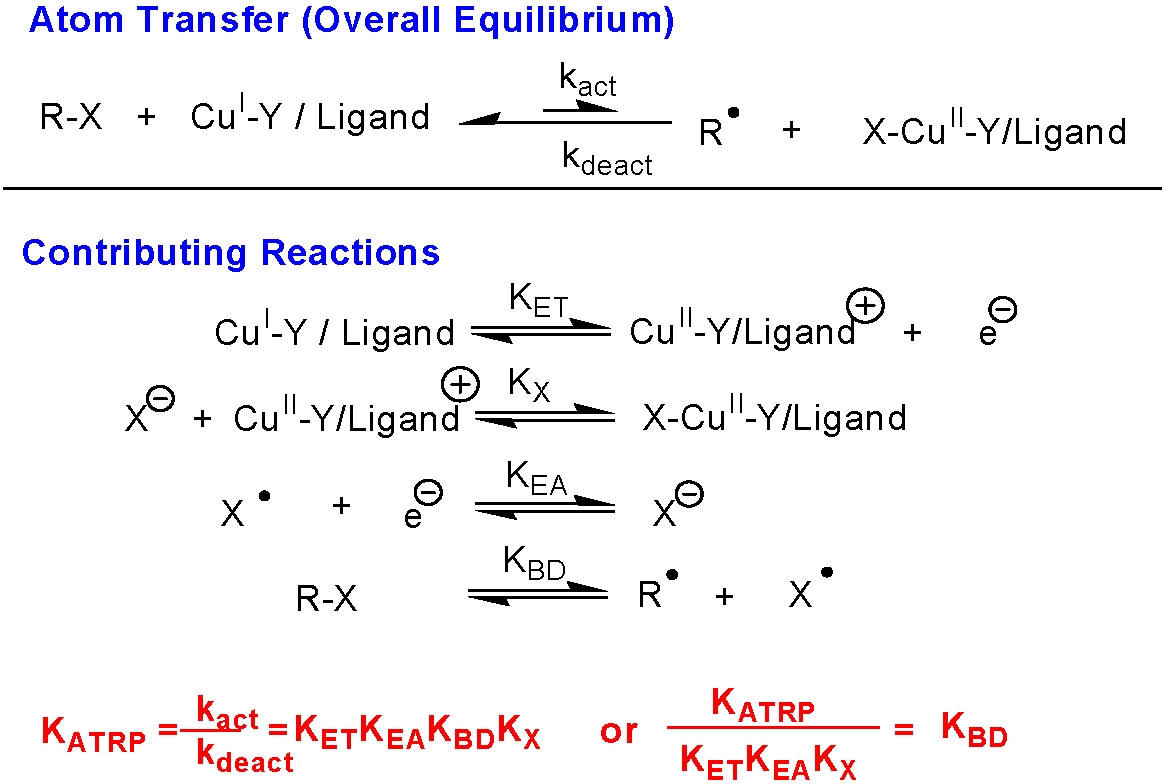
The ATRP equilibrium, (KATRP in the scheme above), is expressed as a combination of several contributing reversible reactions, including a combination of C-X bond homolysis of the alkyl halide (RX), (other transferable atoms or groups can participate in an ATRP(2) but the most frequently employed radically transferable atoms are halogens and will be used to exemplify ATRP throughout most of following discussions) two redox processes, and heterolytic cleavage of the CuII-X bond.
Therefore KATRP can be expressed as the product of the equilibrium constants for electron transfer between metal complexes (KET), electron affinity of the halogen (KEA), bond dissociation energy of the alkyl halide (KBD) and the equilibrium constant for the heterolytic cleavage of the Mtn+1-X bond (KX), which we have named the "halidophilicity" of the Mtn+1-X complex.
This means that for a given alkyl halide R-X, the activity of the catalyst in the ATRP process depends not only on the redox potential, but also on the halidophilicity of the transition metal complex. For complexes that have similar halidophilicity, the redox potential can be used as a measure of catalyst activity in the ATRP. This was demonstrated by the linear correlation between KATRP and E1/2 (i.e. KET) for a series of CuI complexes with nitrogen based ligands.(3,4)
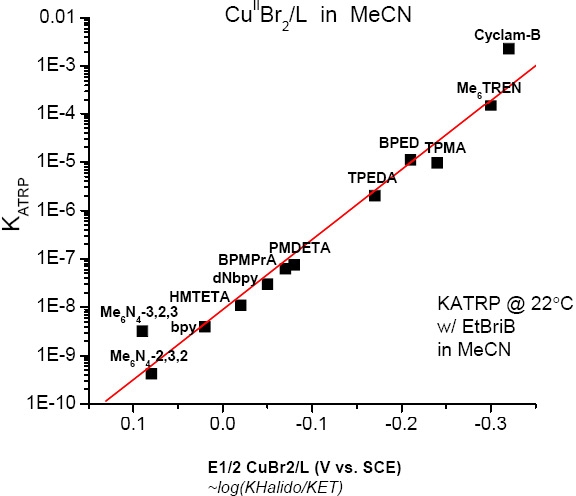
It can also be concluded that for a given catalytic system in the same solvent (where KET, KEA, and KX are essentially constant), KATRP should depend only upon the energetics of alkyl halide bond homolysis, or KBD. Indeed, when the alkyl halide bond dissociation energies were calculated recently for a series of ATRP monomers/initiators, they were found to correlate well with measured values of KATRP.(3)
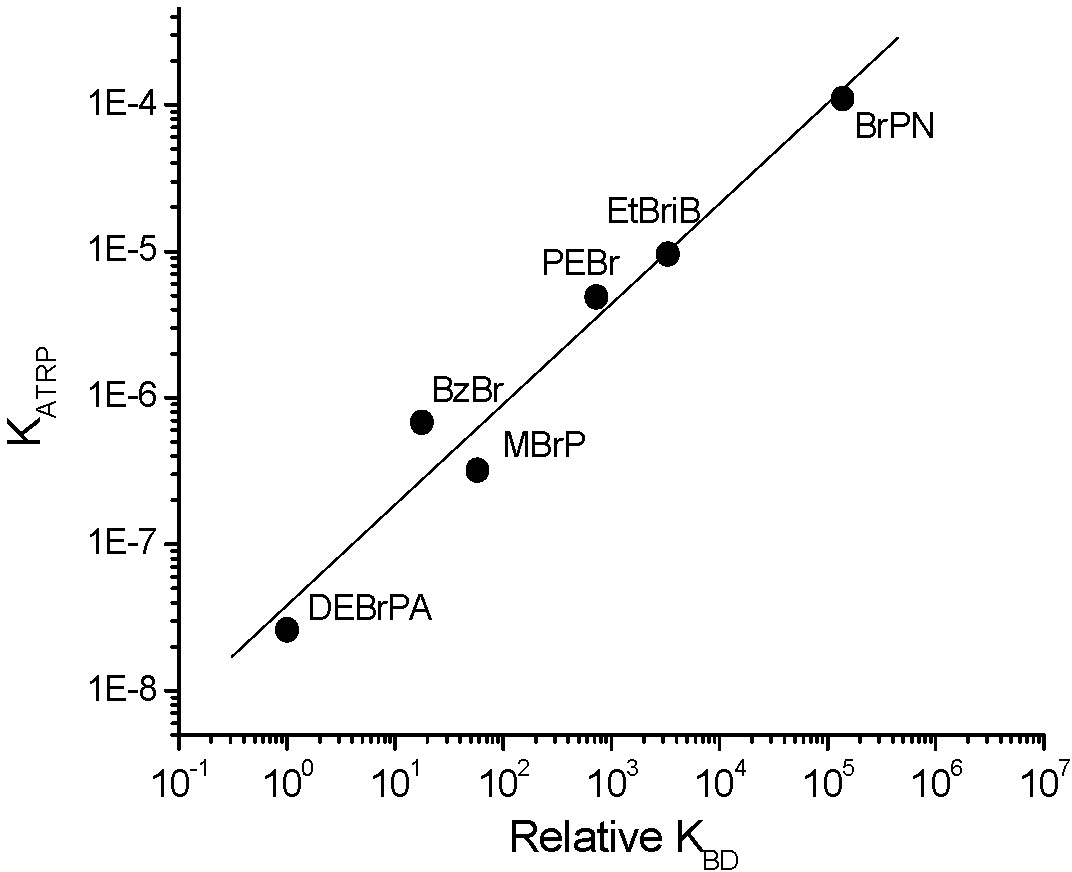
KATRP in the above plot was measured at 22 ºC with CuBr/TPMA; relative values of KBD determined from free energies calculated using DFT; BrPN = bromopropionitrile, BzBr = benzyl bromide, DEBrPA = N,N-Diethyl-α-bromopropionamide, EtBriB = ethyl 2-bromoisobutyrate, PEBr = 1-(bromoethyl)benzene, MBrP = methyl 2-bromopropionate.
It was proposed that such calculations could also be used to predict equilibrium constants for less reactive monomers. Knowing KBD (which can be calculated using DFT) as well as the rate constants of propagation for a given monomer, the rates of polymerization could be calculated for different monomers in ATRP under comparable conditions (same catalyst, constant KET, KEA, and KX). For example, if the ATRP of acrylonitrile reached 90% conversion in 1 second, methyl acrylate requires 4 hours, while styrene would take 22 hours and vinyl acetate 30 years under the same conditions.(3)
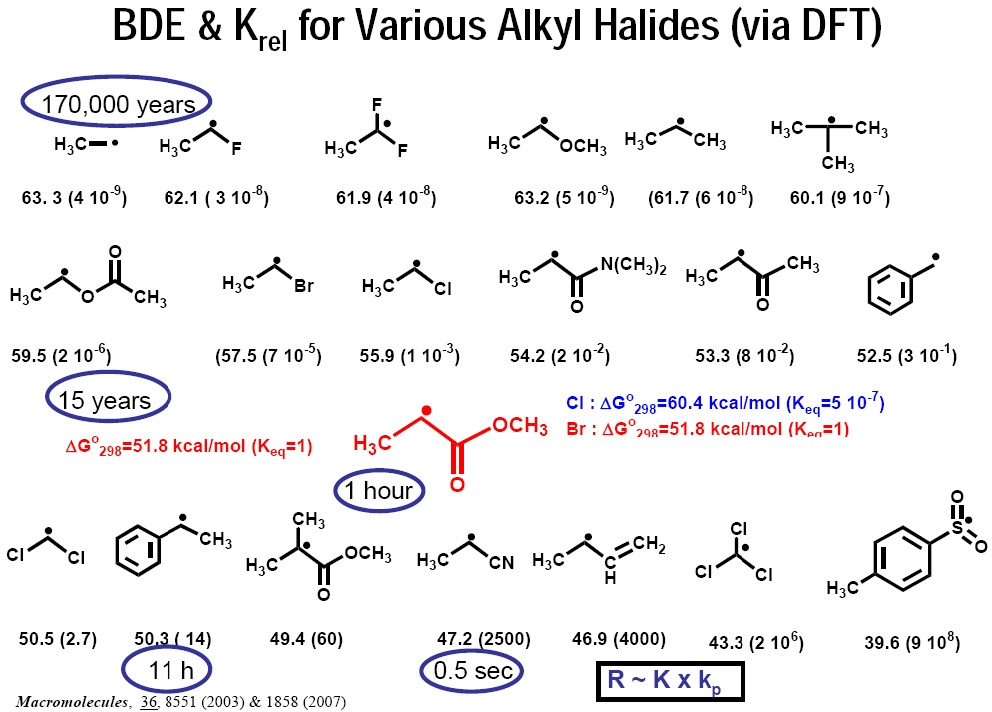
This calculation merely serves to demonstrate the necessity of choosing an appropriate catalyst for each monomer.
Determination of the equilibrium rate constant is crucial in order to understand the kinetics of an ATRP. Assuming steady-state kinetics, the rate of polymerization is given by:![]()
This equation means that the rate of polymerization is controlled by the ratio of CuI to CuII and not the absolute amount of catalyst present in the reaction medium.
Understanding the implications of this equation contributed to the development of ARGET ATRP once the concept of AGET ATRP was developed. Experimentally, the values of KATRP can be determined by direct analysis of the polymerization mixture (by EPR, NMR, GC, GPC, IR...) or by the study of low molecular weight model compounds. Furthermore, while some side reactions (thermal-initiation of monomer, elimination reactions, transfer reactions, degradation of the catalyst...) and some physical parameters (viscosity, inhomogeneity,...) may have an important effect on the kinetics of CRP the influence of these parameters may also be investigated by model studies or by computer simulation.(5-7)
Historically,(8) we considered that the persistent radical effect (PRE) was the primary contributor to the degree of control seen in ATRP and that the PRE operated with some differences between lower activity catalysts and high activity complexes. For example, when Klumperman and Fischer(9) examined polymerization of MMA in the presence of a copper complex formed with N-(n-hexyl)pyridylmethanimine the results showed that adding CuII to the initial reaction mixture can have strong effects on the kinetics of the ATRP depending on the [CuII]0/[CuI]0 ratio. When 10% CuII relative to CuI was added at the beginning of the polymerization, the kinetics were described by Fischer's equation (where ln([M]0/[M]) varies with t2/3) with the reaction orders for initiator, Cu(I) and Cu(II), close to, or the same as, those in Fischer's equation, verifying the applicability of Fischer's equation in lower activity ATRP systems.
On the other hand, when [CuII]0/[CuI]0 ≥ 0.1, the kinetics can be interpreted by Matyjaszewski's equation (ln([M]0/[M]) which varies with t). The polymerization rate almost shows first order kinetics with respect to the concentration of the initiator and CuI and inverse first order with respect to the concentration of CuII, suggesting that the "self-regulation" and radical termination becomes less important for the ATRP process when sufficient CuII is added at the beginning of the reaction. This result confirms the potential for better control of ATRP systems and possibility of reducing or eliminating "wastage" of initiator molecules undergoing coupling reactions to form the equivalent to the persistent radical in an ATRP.
Recently new equations were derived for the evolution of the persistent radical over time for both non-equimolar and equimolar ATRP reactions. From these new equations, KATRP values were obtained for several ATRP systems using UV-vis spectrometric or GC measurements. Fischer's original equations for the PRE could be used only for systems that formed low amounts of persistent radical and consequently operated for systems with relatively low KATRP values. For systems that were driven to higher conversion, and/or more Cu(II) was formed, and for more reactive systems, significant deviations from linearity in t1/3 plots are observed.(10)
kact
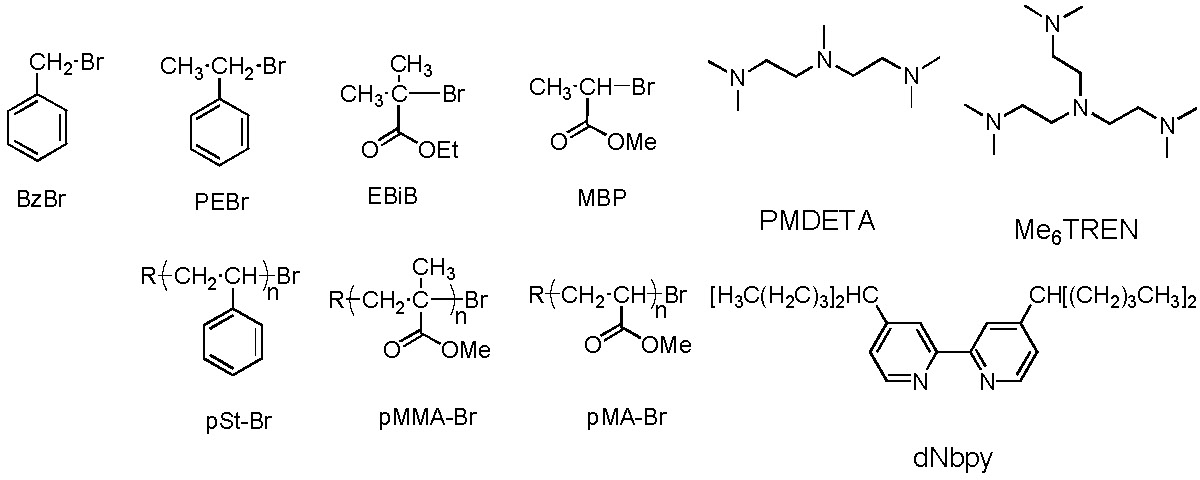
The initial report on determination of the rate constant for activation (kact) for different models of the polymerization system employed both small molecule and macromolecular model initiating species. The structures of the reagents shown in the following schematic describe a few of the ligands and model compounds selected to mimic the polymeric chain ends used in the kinetic studies.(11)
The activation rate constants were measured using HPLC or GC under the kinetic isolation conditions achieved by trapping the generated radical with a ten fold excess of 2,2,6,6-tetramethylpiperidinyl-1-oxy (TEMPO) with respect to the alkyl halide as shown below.(12)
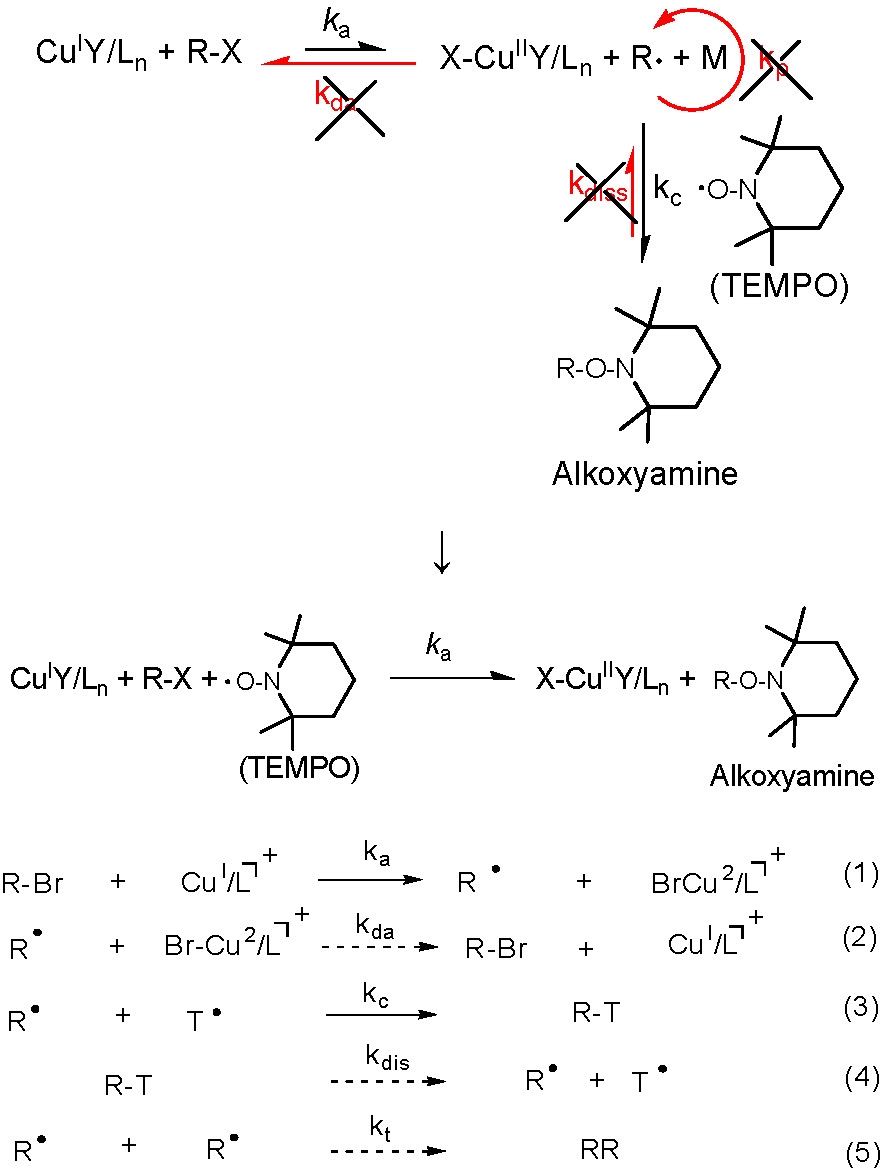
Typical values of the activation rate constants measured at 35 oC indicated that 2-bromoisobutyrate is approximately 10 times more reactive than the other alkyl halides and 1-phenylethyl bromide is ~20 times more reactive than the corresponding chloride.(3) This difference dramatically decreases at higher temperatures due to the higher activation energy for the latter.
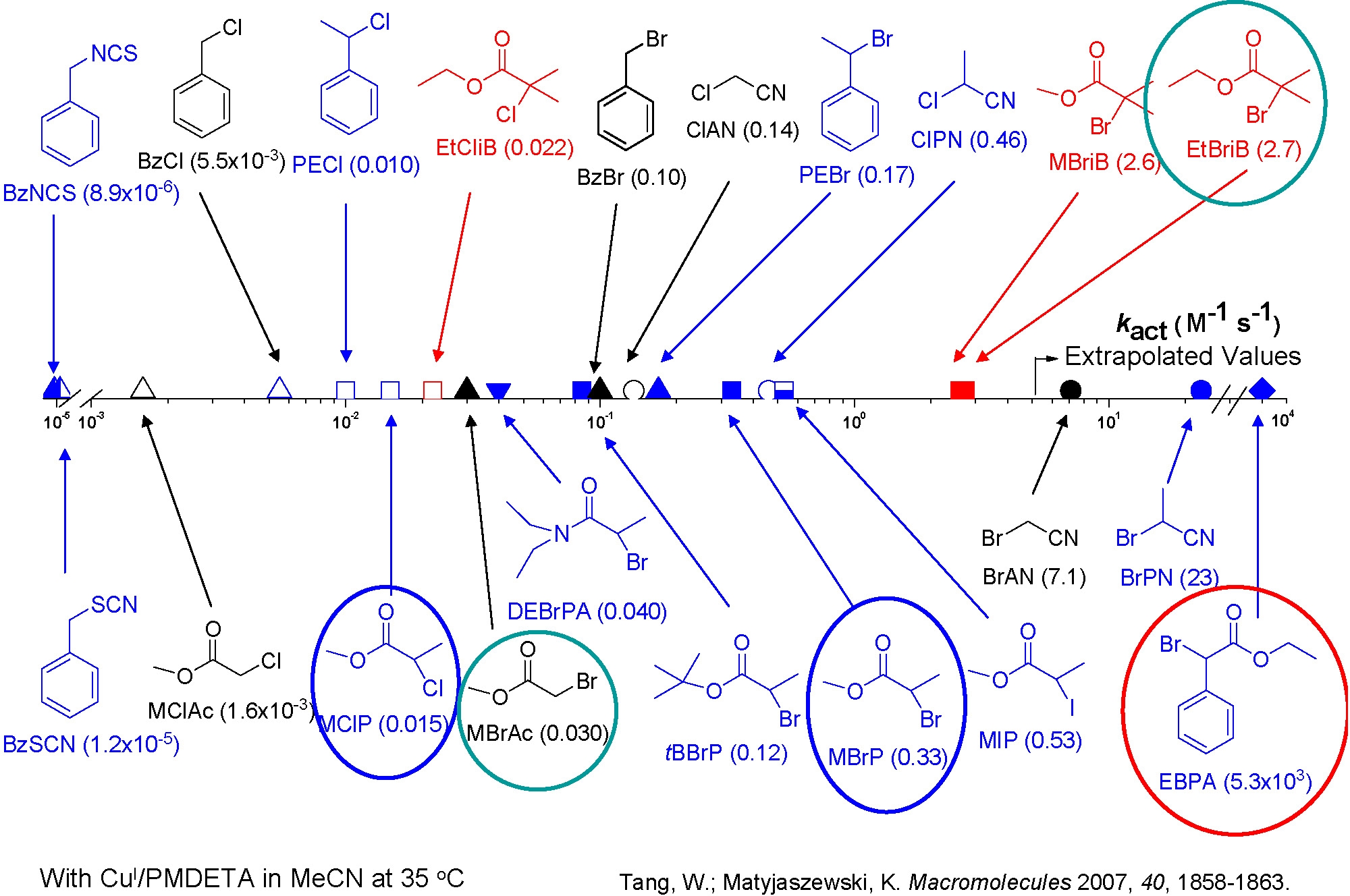
Scheme showing the effect of initiator structure on kact
PMDETA forms more reactive Cu(I) complexes than dNbpy. Me6TREN is ~104 times more active than the dNbpy-based complex. Indeed we have measured differences in activity of copper based catalyst complexes with different ligands that cover a range of 107.(13)
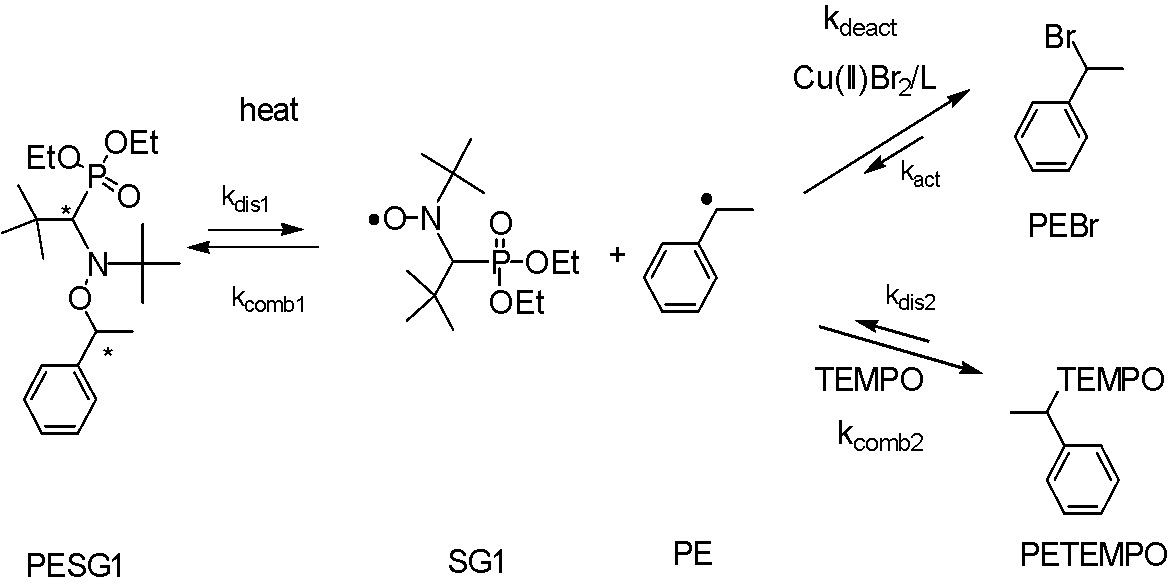
kdeact
Deactivation rate constants were determined by trapping 1-phenylethyl radicals using TEMPO in a competitive clock reaction. The 1-phenylethyl radical was generated by the thermal decomposition of the 1-(N,N-(2-methylpropyl-1)-(1-diethylphosphono-2,2-dimethyl-propyl-1-)-N-oxyl)-1-phenylethane (PESG1).(12) The alkoxyamine can be obtained from Arkema under the trade name BlocBuilderTM and is one of the most versatile control agents available for NMP.
[Arkema website: http://www.arkema-inc.com/index.cfm, then select products and under product selection choice you will see the information.]
Another method for the estimation of deactivation rate constants in ATRP using copper catalysts is based on the principle of reverse ATRP and is conducted under an air atmosphere, using molecular oxygen as an oxidant for the Cu(I) species.(14) The deactivation rate constants for several different reactive copper complexes were estimated by this procedure, and the results correlated with those obtained from the analysis of the evolution of molecular weight distribution with conversion and the results agreed well with competitive trapping reactions using nitroxides.
REFERENCES
(1) Braunecker, W. A.; Matyjaszewski, K. Progress in Polymer Science 2007, 32, 93-146.
(2) Davis, K. A.; Matyjaszewski, K. Journal of Macromolecular Science, Pure and Applied Chemistry 2004, 41, 449-465.
(3) Tang, W.; Matyjaszewski, K. Macromolecules 2007, 40, 1858-1863.
(4) Tang, W.; Kwak, Y.; Braunecker, W.; Tsarevsky Nicolay, V.; Coote Michelle, L.; Matyjaszewski, K. J Am Chem Soc 2008, 130, 10702-10713.
(5) Matyjaszewski, K.; Nanda, A. K.; Tang, W. Macromolecules 2005, 38, 2015-2018.
(6) Knuehl, B.; Pintauer, T.; Kajiwara, A.; Fischer, H.; Matyjaszewski, K. Macromolecules 2003, 36, 8291-8296.
(7) Pintauer, T.; Braunecker, W.; Collange, E.; Poli, R.; Matyjaszewski, K. Macromolecules 2004, 37, 2679-2682.
(8) Matyjaszewski, K.; Patten, T. E.; Xia, J. J. Am. Chem. Soc. 1997, 119, 674-680.
(9) Zhang, H.; Klumperman, B.; Ming, W.; Fischer, H.; van der Linde, R. Macromolecules 2001, 34, 6169-6173.
(10) Tang, W.; Tsarevsky, N. V.; Matyjaszewski, K. Journal of the American Chemical Society 2006, 128, 1598-1604.
(11) Matyjaszewski, K.; Goebelt, B.; Paik, H.-j.; Horwitz, C. P. Macromolecules 2001, 34, 430-440.
(12) Matyjaszewski, K.; Paik, H.-j.; Zhou, P.; Diamanti, S. J. Macromolecules 2001, 34, 5125-5131.
(13) Tang, W.; Kwak, Y.; Braunecker, W.; Tsarevsky, N. V.; Coote, M. L.; Matyjaszewski, K. J. Am. Chem. Soc. 2008, 130, 10702-10713.
(14) Gromada, J.; Matyjaszewski, K. Macromolecules 2002, 35, 6167-6173.
Determination of the Redox Potential of Copper Complexes
In this section of the page we discuss the role of the coordinating ligand in the catalyst complex and its effect on catalyst activity. We are interested in the redox behavior of copper complexes that could be used in an ATRP, and how the redox potential is dependent on the complex forming ligand and on the reaction media.
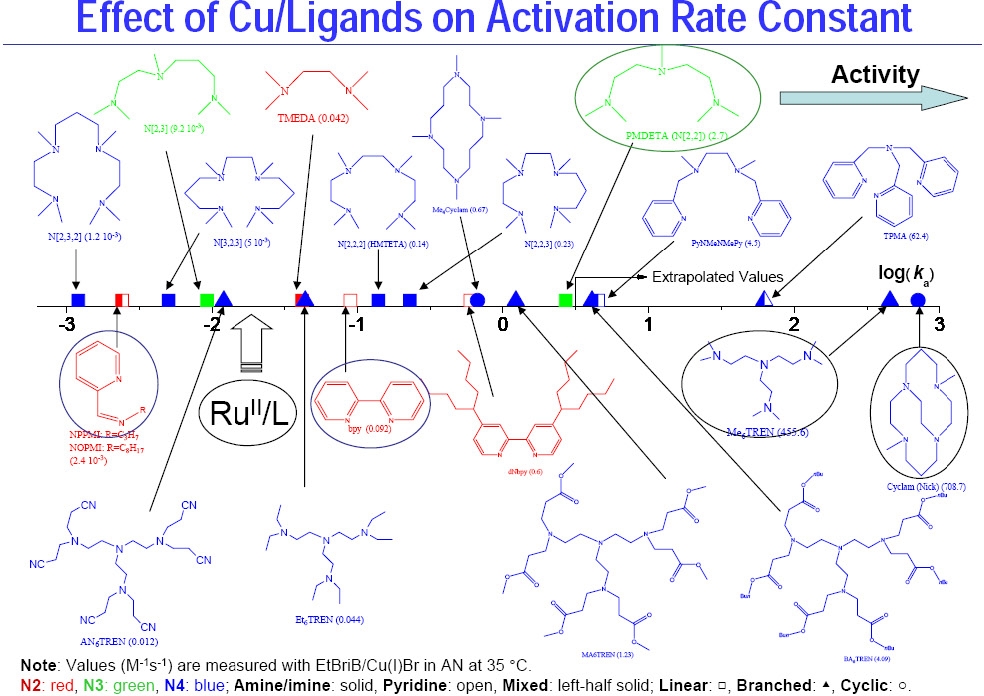
Cyclic voltametry of copperI and copperII complexes are used to measure the redox potentials. For Cu(I) complexes with nitrogen based ligands KATRP is proportional to E1/2. More reducing catalysts increase KATRP. The redox potential and halidophilicity of the catalyst are affected by both the transition metal and ligand. Generally, the more reducing the catalyst complex is, the more active the catalyst. The order of activity is shown below for a selection of N-based ligands.
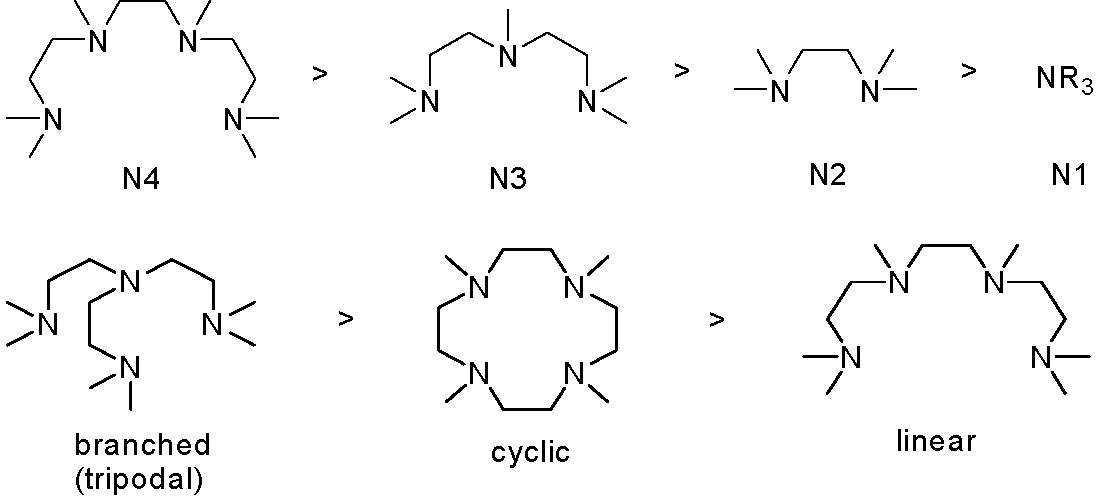
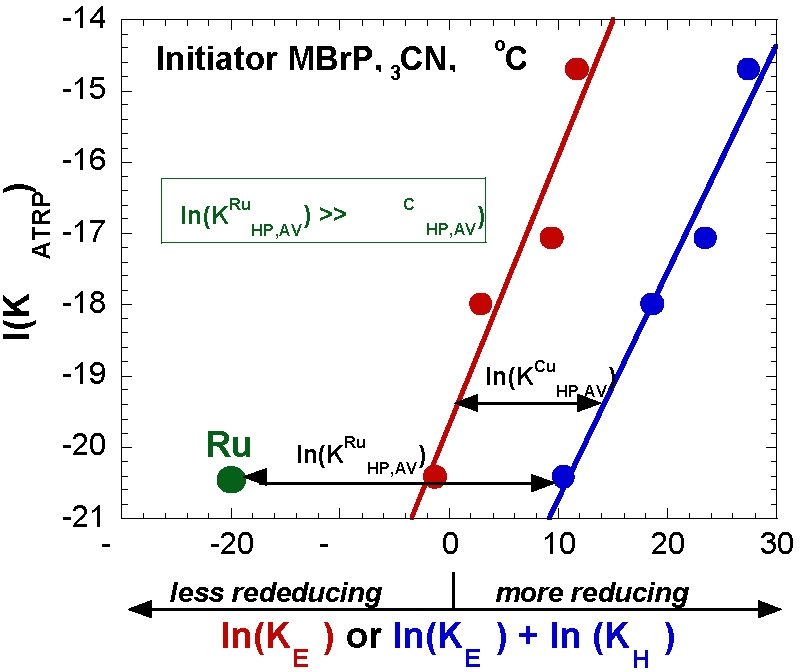
The reduction potentials can be correlated with kact and kdeact for the activation of 1-PhEtBr and deactivation of PhEt·. The deactivation rate constants scale reciprocally with activation rate constants.
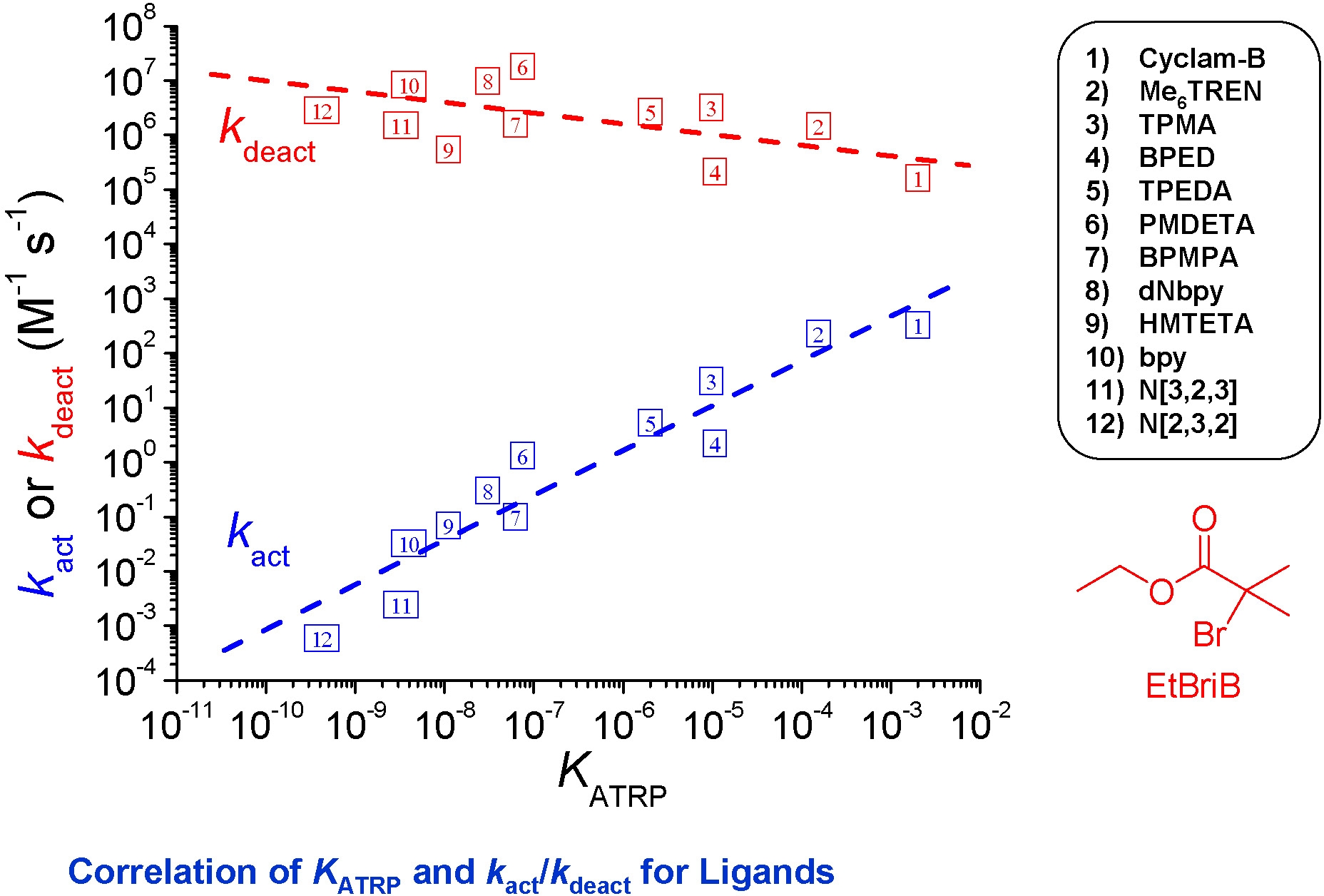
The catalyst complex formed with Me6TREN has a very high kact AND a sufficiently high kdeact making Me6TREN a VERY efficient ligand, especially for less reactive monomers.
One reason for the high activity of the TREN based catalyst complexes is that entropy favors a high kdeact for Me6TREN since the CuII atom moves just 0.13 Å inside the cavity of the ligand.(1,2) While most work on (TREN) based ligands has been conducted using Me6TREN as the ligand the substituents on the N-atoms of the commercially available H6TREN can be readily modified using a Michael addition to attach different species to H6TREN to prepare ligands suitable for catalysts that will be soluble in different polymerization environments, control the rate of polymerization and be easy to remove from the product. The figure also shows that different substituents on the ligand can significantly affect activity; cf. activity of Me6TREN with Et6TREN.(3)
H6TREN is available in commercial quantities from Pressure Chemicals,
http://www.presschem.com/specialties/Tris(2-aminoethyl)amine.htm
and Me6TREN is available from ATRP Solutions.
http://atrpsolutions.com/includes/PB_3%20Ligands.pdf
The structure of some of the other ligands examined in this study(4) and the relative activity of their Cu complexes are shown below:
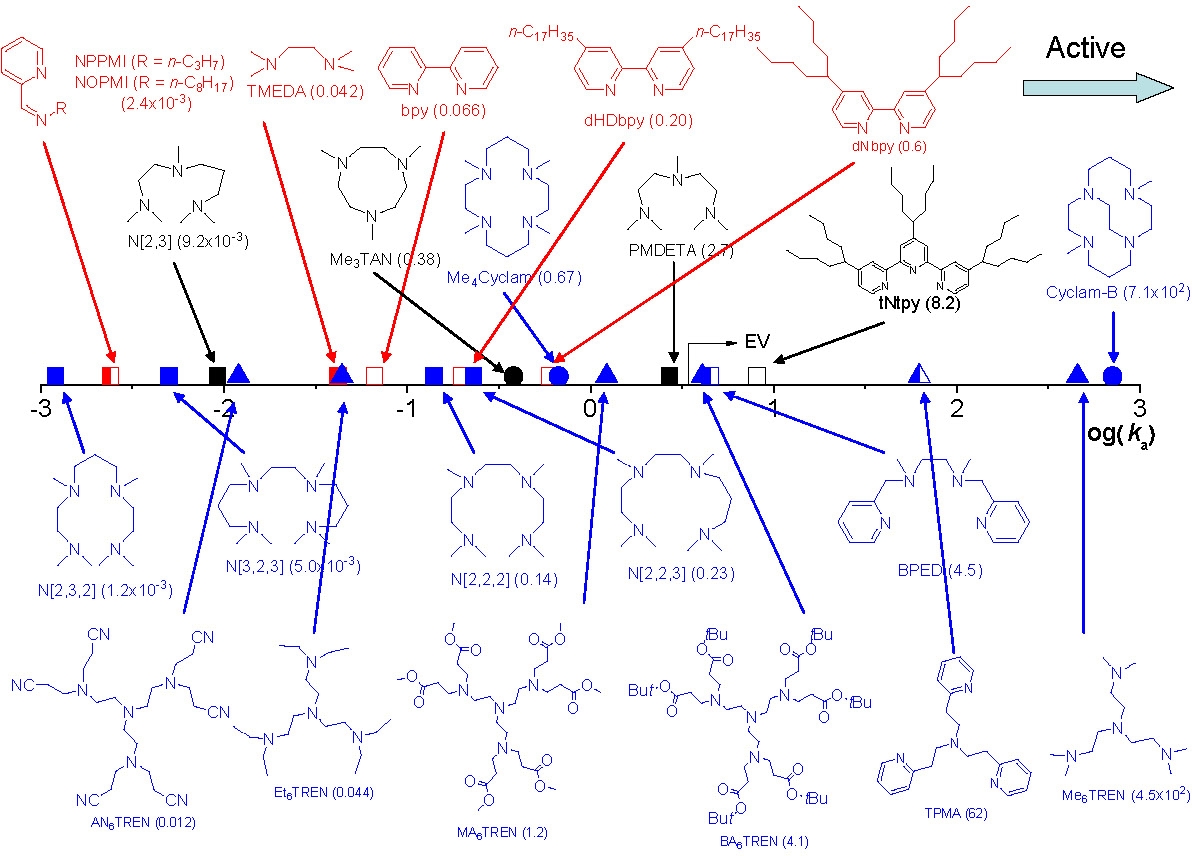
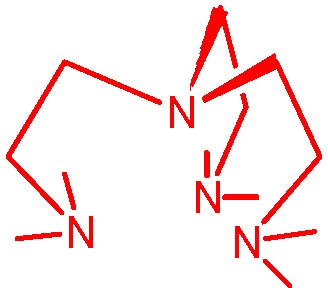
The most active ATRP catalyst reported to date, the Cu complex dimethyl cross-bridged cyclam,(5) was identified solely based on its very low reduction potential (> 75 mV lower than that of the CuBr /Me6TREN complex).
The range of activity of catalyst complexes with different ligands therefore exceeds one million. This figure clearly indicates that conditions optimized for one catalyst complex, e.g. a pyridine-imine (NPPMI) based catalyst complex, can not be used for complexes employing Me6TREN as ligand or indeed even bpy, since the activity between the complexes differ by orders of magnitude. These differences do not indicate different polymerization mechanisms are operating, only that the reactions conditions have to be modified to take into account the different activity of the selected catalyst complex.
The general order of activities of Cu complexes is related to their structure and follows the following order: tetradentate (cyclic-bridged) > tetradentate (branched) > tetradentate (cyclic) > tridentate > tetradentate (linear) > bidentate ligands. The nature of the N atom is also important and follows the order: pyridine ≥ aliphatic amine > imine. The link between the N-atoms is also important with C2 > C3 >> C4.
As seen from the above figure the activity of a given Cu complex strongly depends on the ligand structure and even small structural changes may lead to large differences in their activity. Note effect of different substituents on the activity of TREN-based ligands. In addition to changing the phylicity of the resulting complex the different substituents dramatically change the activity, resulting in formation of catalyst complexes with activity spanning 5 orders of magnitude, from the lower activity of AN6TREN to high activity with Me6TREN.
Recently a new, versatile and highly active copper-based complex CuBr/N,N,N',N'-tetrakis(2-pyridylmethyl)ethylenediamine (TPEN) was reported for ATRP of acrylic, methacrylic, and styrenic monomers.(6) The catalyst mediated ATRP at a catalyst/initiator molar ratio of 0.005 and produced polymers with well-controlled molecular weight and low polydispersity. ATRP occurred even at a catalyst/initiator molar ratio as low as 0.001; i.e., with copper concentration in the produced polymers as low as 6-8 ppm, (catalyst/monomer molar ratio = 105). The catalyst structures were studied by X-ray diffraction and NMR spectroscopy. The activator CuIBr/TPEN existed in solution as an equilibrium mixture of binuclear and mononuclear complexes but as a binuclear complex in single crystals. The deactivator CuIIBr2/TPEN complex was mononuclear.
High stability and appropriate KATRP were found crucial for catalysts required to work under high dilution or in the presence of coordinating solvents/monomers.
This provides guidance for further design of highly active ATRP catalysts.
REFERENCES
(1) Becker, M.; Heinemann, F. W.; Schindler, S. Chem.--Eur. J. 1999, 5, 3124-3129.
(2) Di Vaira, M.; Orioli, P. Acta Crystallogr., Sect. B 1968, 24, 595-599.
(3) Gromada, J.; Spanswick, J.; Matyjaszewski, K. Macromolecular Chemistry and Physics 2004, 205, 551-566.
(4) Tang, W.; Matyjaszewski, K. Macromolecules 2006, 39, 4953-4959.
(5) Tsarevsky, N. V.; Braunecker, W. A.; Tang, W.; Brooks, S. J.; Matyjaszewski, K.; Weisman, G. R.; Wong, E. H. Journal of Molecular Catalysis A: Chemical 2006, 257, 132-140.
(6) Tang, H.; Arulsamy, N.; Radosz, M.; Shen, Y.; Tsarevsky, N. V.; Braunecker, W. A.; Tang, W.; Matyjaszewski, K. Journal of the American Chemical Society 2006, 128, 16277-16285.
