Shila Banerjee's group integrates theory, simulations, and data-driven modelling to understand how physical forces and chemical signalling control the shapes and architecture of living cells. They use concepts from statistical physics and dynamical systems to understand the principles that guide the organization and mechanics of sub-cellular matter, and predict how changes in sub-cellular organization control the spatiotemporal patterns of growth and movement in cells and tissues.

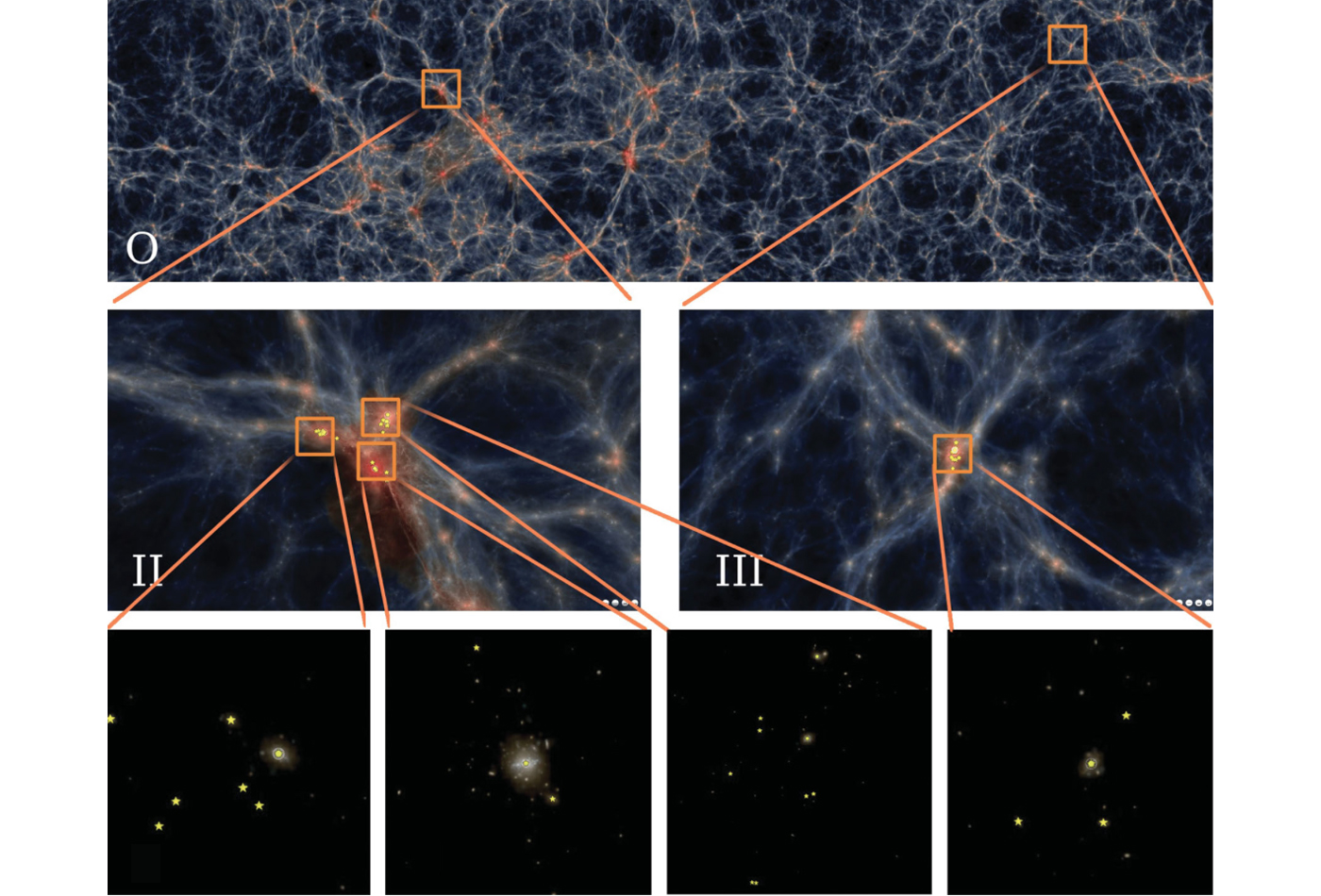
Rupert Croft simulates the growth of structure in the Universe including gravitational, hydrodynamic and radiative effects. The physical processes are complex, non-linear and interlinked. Analyzing the data from these models can explain the growth of stars, galaxies and larger structures.

Markus Deserno uses both theoretical and computational techniques to study lipid membranes. On the theoretical side, a continuum elastic description is used, and on the computational side, coarse-grained simulations in which the physical system is not represented in atomic detail are utilized. This renouncement of chemical resolution allows one to study much larger systems on much longer time scales and to access a new arena for physical questions, many of which turn out to have biological significance.

Tiziana Di Matteo's research focuses on the formation and growth of black holes, and their interaction with galaxies and the rest of the Universe. Massively parallel hydrodynamic simulations are necessary to follow the gas dynamics, radiative cooling and gravitational evolution of hundreds of millions of mass elements. One of her current projects involves simulating the growth of black holes in the full cosmological context, starting from small fluctuations after the Big Bang and following the evolution of the Universe to the present day.

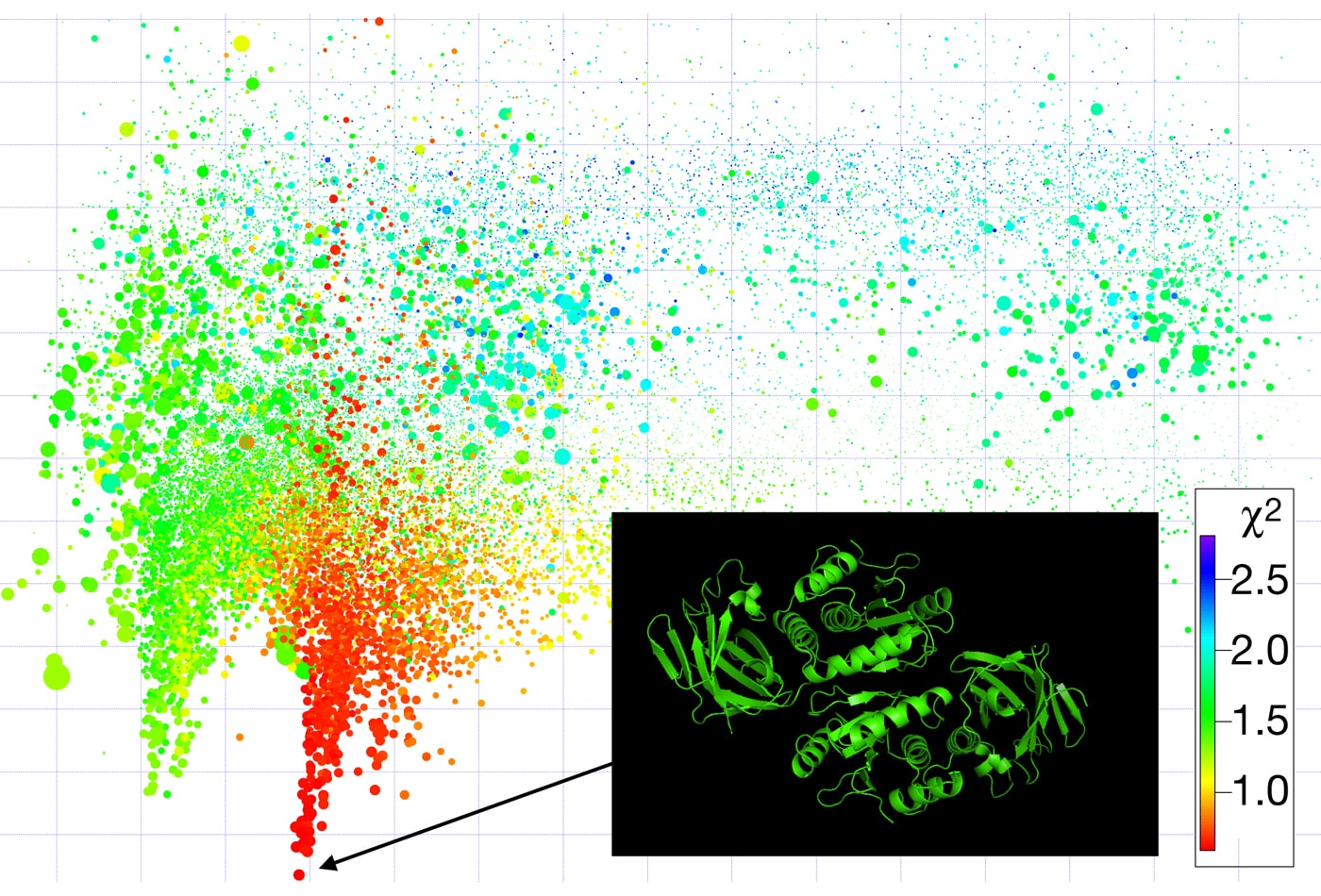
Frank Heinrich uses supercomputing resources for Monte Carlo Markov chain-based data modeling and the quantitative assessment of the information content of experimental data in neutron scattering.

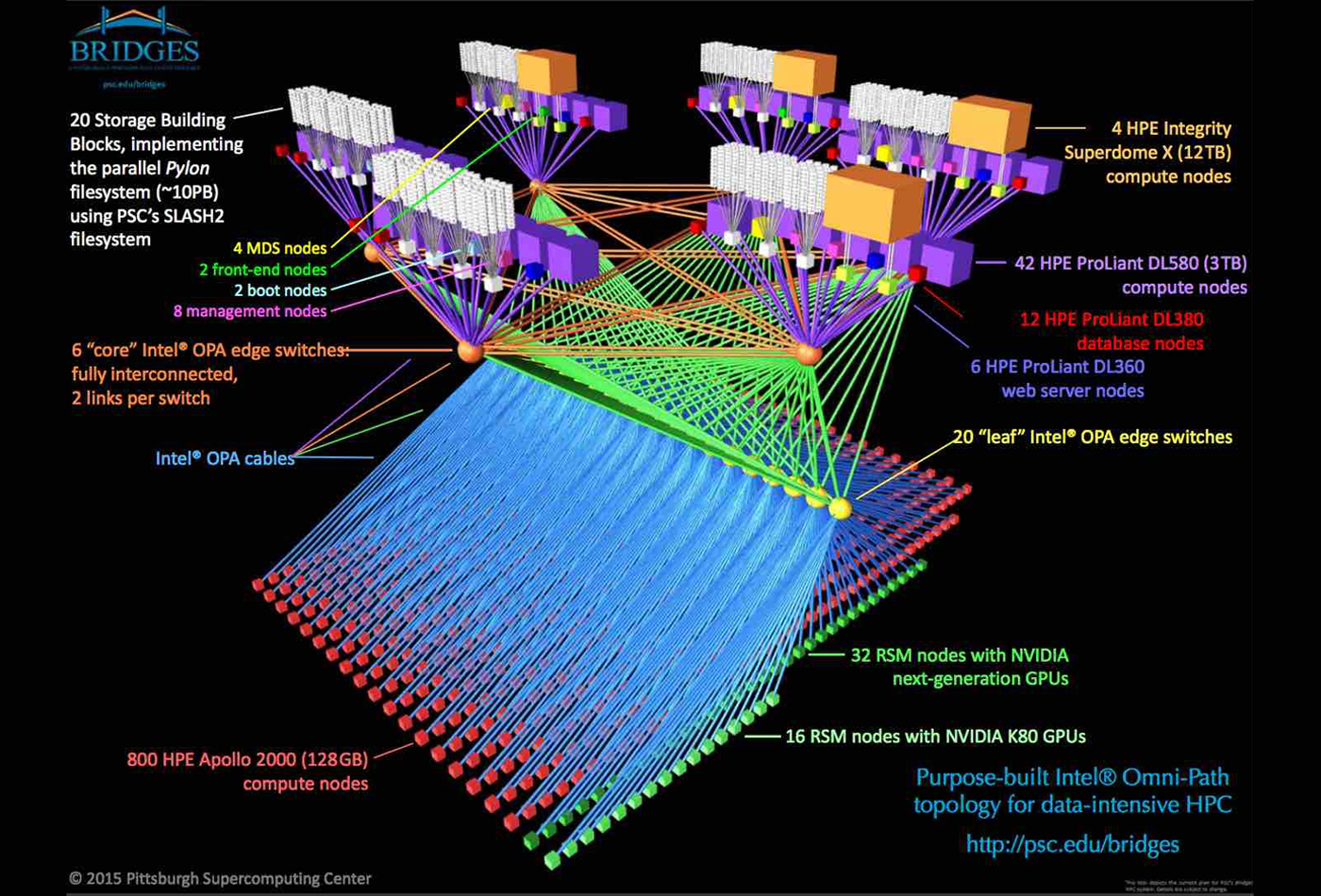
Michael Levine (Emeritus) is the former co-director of the PITTSBURGH SUPERCOMPUTING CENTER. He developed computational hardware and numerical and algebraic algorithms to perform high order perturbative calculations in quantum electrodynamics.

Curtis Meyer's computational activities revolve around experimental studies of hadrons (particles built from quarks and antiquarks). The techniques employed are amplitude and partial wave analysis. Current activities are focused on the analysis of data from a Jefferson Lab (JLab) experiment which is used to search for baryons (excited partners to the familiar proton and neutron) in very large data sets.

Colin Morningstar uses lattice quantum chromodynamics (QCD) to investigate hadron formation and quark confinement. He has computed the mass spectrum of glueballs in the Yang-Mills theory of gluons, studied the excitation spectrum of the effective QCD string between a static quark-antiquark pair, and produced the first glimpse of the nucleon excitation mass spectrum from QCD. He is a member of a large nationwide collaboration of lattice QCD theorists dedicated to Monte Carlo calculations of QCD observables on large-scale computing clusters. He and Curtis Meyer built and maintain the CMU QCD cluster.

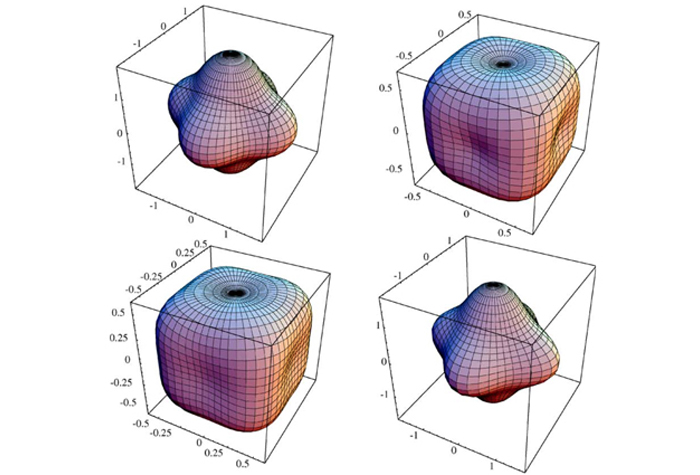
Robert Sekerka (Emeritus) solves partial differential equations representing crystal growth to understand morphological instabilities leading to cellular and dendritic structures. Other interests include development of lattice-Boltzmann techniques to simulate solutions of the Navier-Stokes equations of hydrodynamics.

Robert Swendsen (Emeritus) develops computational algorithms for the efficient simulation of phase transitions and novel data analysis techniques to extract information from these simulations. Additional work addresses methods for efficient simulation of biological molecules.

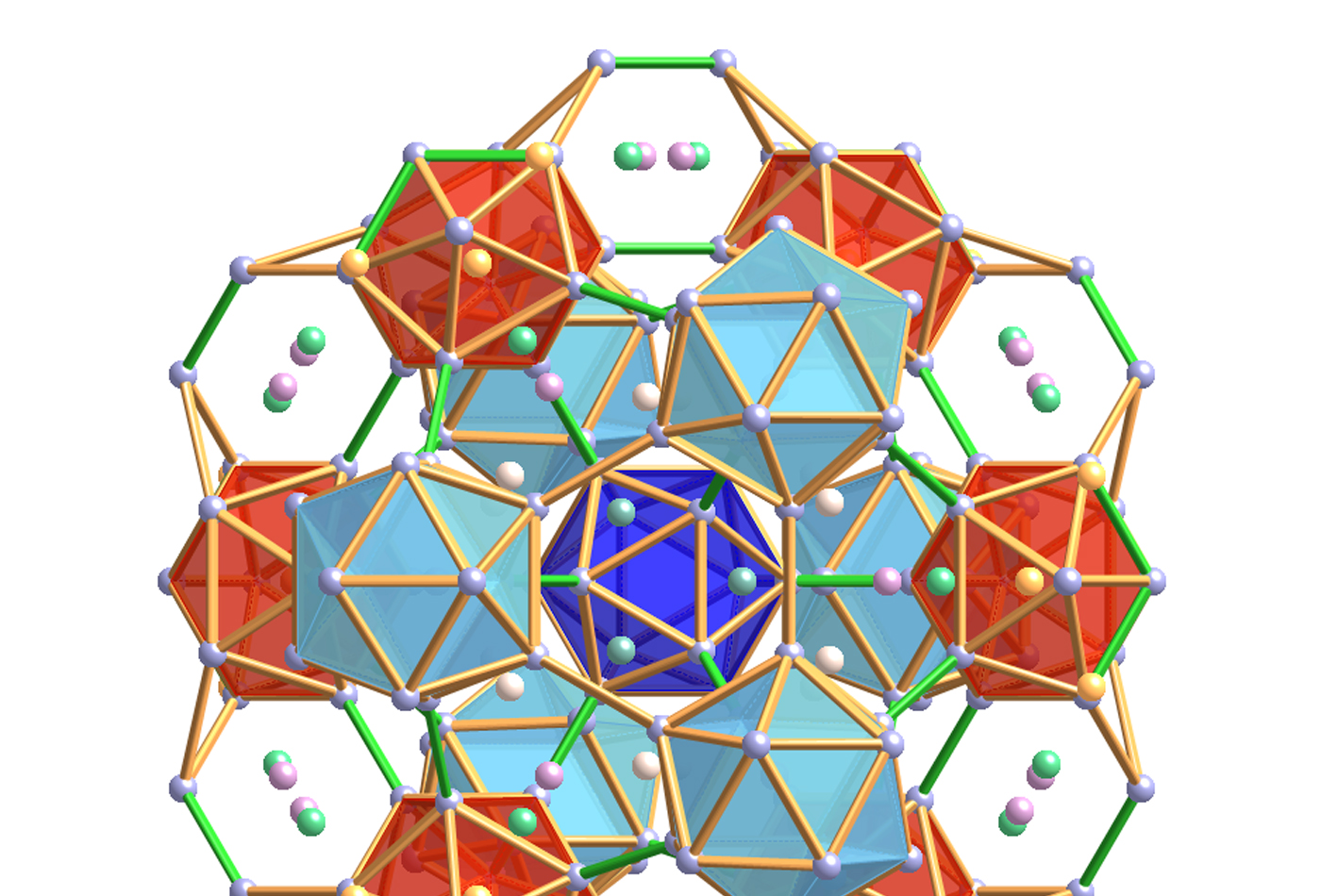
Michael Widom carries out Monte Carlo and molecular dynamics simulations of metal alloys and employs ab-initio methods for band structure and total energy calculation. Current areas of interest include high entropy alloys and other complex and intrinsically disordered structures such as borides, quasicrystals and metallic glasses.