CMU Mathematics Undergraduate Research, 2023

In early 2020, as the global coronavirus pandemic brought the world to a screeching halt, many of our students found that their summer programs had been cancelled. Many of these students were very interested in using this suddenly free summer to engage with open ended-projects in mathematics. In response to this demand, the Department of Mathematical Sciences curated a brand new summer program: Summer Experiences in Mathematical Sciences (SEMS). This program is offered in parallel with the traditional SURF program, which provides stipends to students who stay at CMU in the summer months to work on research projects. Find below details of the projects conducted in the summer of 2023 under the auspices of the SURF and SEMS program.
▼ SURF projects
► Analysis of a simplified War-like card game
Adam Bertelli
Advisor: Boris Bukh
Abstract: The game of War is a card game popular among children worldwide. We study the variant in which all cards are of distinct rank and each player's deck is shuffled after each turn. This continues our work from the last summer. We derive stronger upper bounds on the expected length of such a game, and clarify the previous coupling arguments.
► Bounding Lifts of Markoff Triples mod $p$
Brenda (Siran) Chen
Advisor: Elisa Bellah
Abstract: In 2016, Bourgain, Gamburd, and Sarnak proved that Strong Approximation holds for the Markoff surface in most cases. That is, the modulo $p$ solutions to the equation $x^2+y^2+z^2=3xyz$ are covered by the integer points for most primes $p$. To prove this result, Bourgain, Gamburd, and Sarnak constructed a path in the associated Markoff mod $p$ graphs. In this project, we implemented this path finding algorithm in order to obtain upper bounds on lifts of Markoff triples modulo $p$. We then collected numerical evidence that these bounds can be improved on average and with high probability.

► Multivariate Gaussian Mixtures
Brandon Dong
Advisor: Tomasz Tkocz
Abstract: We say that a random vector in Euclidean space is a (centred) Gaussian mixture if it has the same distribution as a random matrix acting on an independent of it standard Gaussian random vector. We establish the Schur convexity of the moments of weighted sums of independent identically distributed Gaussian mixtures. This extends such results previously known in the scalar case.
► Two-Phase Free Boundary Problems
Thomas Horstkamp
Advisor: Giovanni Leoni
Abstract: This project aims to investigate two-phase free-boundary problems motivated by the flow of two liquids in models of jets and cavities. Specifically, the project considers the minimization of functionals involving a two-phase function and its derivative, subject to boundary conditions.
The existence and regularity of solutions are of interest. Since the study of two-phase free-boundary problems is still in its early stages, this project seeks to contribute to its development by providing more elementary proofs of previously established results and studying novel variations of previous problems. The methodology involves using techniques from the Calculus of Variations, Functional Analysis, and Sobolev Spaces to parameterize critical points of the functionals and reduce to standard minimization problems. The results of this research may have useful real-world applications in modeling physical phenomena and industry-related problems.
► Solitary waves in infinite Calogero-Moser lattices
Benjamin Ingimarson
Advisor: Bob Pego
Abstract: In Calogero-Moser particle systems, every particle interacts with every other particle by a force proportional to the inverse cube of the distance between them. Finite Calogero-Moser systems are known to be completely integrable. By a stroke of incredible luck, we find explicit formulas for solitary waves in infinite Calogero-Moser systems as limits of explicit periodic traveling waves.
► Capillary droplets inside a container
Iris Jiang
Advisor: Robin Neumayer
Abstract: The shape of the region occupied by a droplet of liquid inside a container is modeled by an isoperimetric problem, which consists of minimizing Gauss’ free energy among shapes of a fixed volume. This project focuses on a two-dimensional analogue of this model and investigates how the container’s geometry impacts the shape and energy of energy-minimizing liquid droplets. We show that in any non-circular container, when the mass of the droplet is sufficiently small, the minimizing droplet’s energy is strictly smaller than the energy of a droplet of the same mass in a circular container of the same size.
► Stiffness matrices of blow-ups of graphs
Yunseong Jung
Advisor: Alan Lew
Abstract: A $d$-dimensional framework is a pair $(G,p)$ consisting of a graph $G$ and a map $p$ of its vertices into $\mathbb{R}^d$. We can picture this framework as a mechanical structure: we draw each edge of the graph as a straight segment between its two vertices, and think of it as a "solid bar".
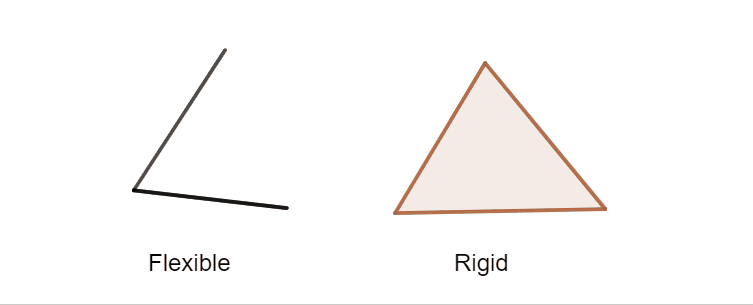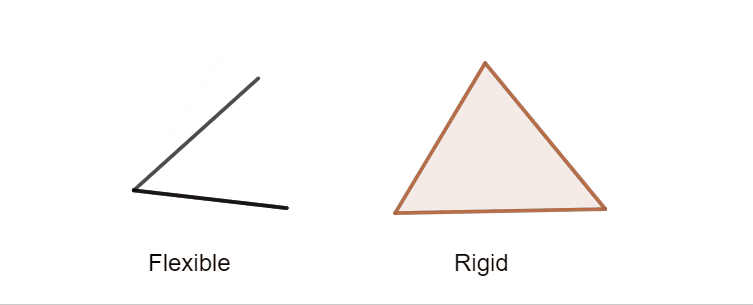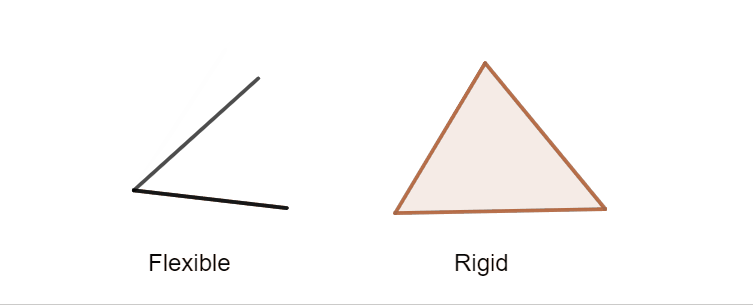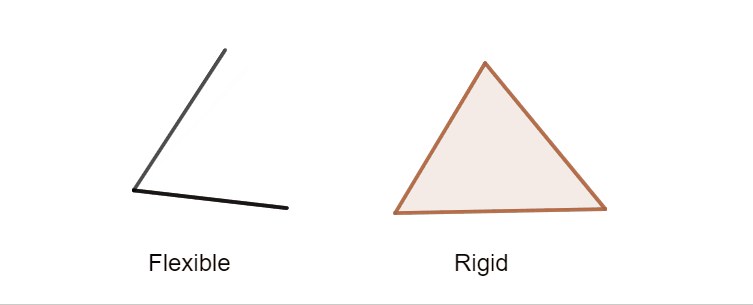
The vertices, in turn, play the role of "hinges" or "joints", around which the solid bars can rotate freely.
We can then ask whether the framework is "flexible" or "rigid" - can this structure be deformed without stretching or bending any of the solid bars?
Recently, Jordan and Tanigawa introduced the notion of $d$-dimensional algebraic connectivity, denoted by $a_d(G)$, which can be seen as a "quantitative measure" of the $d$-dimensional rigidity of $G$, and is defined in terms of the eigenvalues of certain "stiffness matrices" associated to different mappings of $G$ into $d$-dimensional space. The question of determining the value of $a_d(G)$ turns out to be surprisingly difficult, and an exact solution is not known even for some of the simplest examples.
In this project we studied how the eigenvalues of a stiffness matrix change when we replace one or more of the vertices of the graph with several "copies" of themselves. Graphs obtained in this way are called "blow-ups" of the original graph. As an application, we obtained a new lower bound on the $2$-dimensional algebraic connectivity of complete bipartite graphs, and a new simple proof of the computation of the $d$-dimensional algebraic connectivity of generalized star graphs.
► Turbulence and self-homeomorphisms of the Sierpinski carpet
Dhruv Kulshreshtha
Advisor: Aristotelis Panagiotopoulos
Abstract: Let $K$ be a compact metric space and consider the homeomorphism group $H(K)$ of all symmetries of $K$. How difficult is it to classify those symmetries up to conjugacy? If $K$ is the interval $[0,1]$ then $H(K)$ can be easily classified using certain countable structures as invariants: these countable structures have to simply keep track of the maximal open intervals on which each homeomorphism is increasing, decreasing, or constant. The problem becomes much more complex if one is to replace the interval $[0,1]$ with the square $[0,1]^2$. Indeed it is a theorem of Hjorth that there exists no definable way to classify self-homeomorphisms of the square $[0,1]^2$ by using countable structures as invariants. The proof of this result goes through his celebrated theory of turbulence.
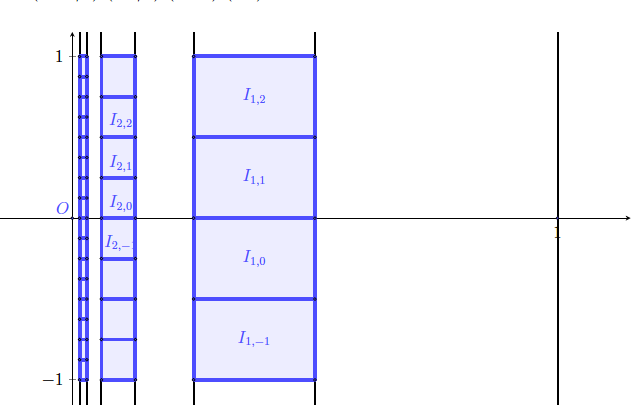
The main goal of this project is to consider the problem of classifying $H(\mathbb{S})$ where $\mathbb{S}$ is the classical one-dimensional Sierpinski Carpet:

► On the complexity of the Problem of Equivalence for Surfaces
Yoojung Christina Kwon
Advisor: Aristotelis Panagiotopoulos
Abstract: The problem of equivalence, which dates back to Gauss and Cartan, has been a subject of study for centuries. The problem asks for simple, necessary and sufficient conditions for deciding when two Riemannian metrics represent the same geometry, albeit in a different coordinate system.
This research project employed modern methods from descriptive set theory to identify the intrinsic complexity of the problem of equivalence in the special case of dimension 2.
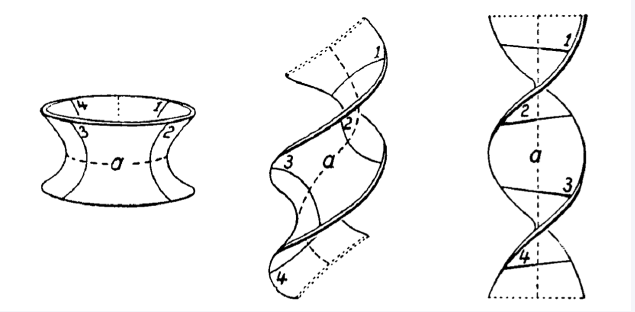
Through this approach, we gained insights as to which invariants can and cannot be used in solving the problem of equivalence. Importantly, the problem of equivalence in dimension 2 is Borel bireducible to the universal countable Borel equivalence relation.
► A generalization of the regulated integral
Subhasish Mukherjee
Advisor: Ian Tice
Abstract: We investigate set-algebra pairs and prove properties about the regulated functions, the uniform closure of the set of step functions in the uniformity of uniform convergence for functions taking values in uniform spaces. In a very elementary way, with respect to finitely additive measures we define the Cauchy integral on the regulated functions taking values in locally convex spaces.
We prove the Cauchy integral satisfies several properties, such as linearity, versions of monotonicity, a Riesz representation theorem, an elementary Fubini theorem, the fundamental theorem of calculus and its standard consequences, and various continuity properties. We apply these properties for regulated functions from $\mathbb{R}^n$ to locally convex spaces and show that this is a robust theory of integration and an alternative to the Riemann or Bochner integrals as a first pass at integration.
▼ SEMS projects
► Collapsibility Thresholds for Geometric Complexes on Spheres
Maxim Grebinskiy, Sophia Yang, Maolinsheng (Iris) Ye
Advisor: Andrew Newman
Abstract: A Vietoris--Rips complex of a point set in $\mathbb{R}^d$ is the simplicial complex obtained by including all subsets of diameter at most some specified value. We studied the Vietoris--Rips complexes formed on $n$ points selected uniformly at random from the $d$-sphere $S^d$. We were especially interested in proving collapsibility results; that is results about when it is possible to reduce the dimension of the complex without changing critical topological properties. On $S^1$, we proved a coarse threshold for the random complex to be $1$-collapsible, and for $S^d$ where $d \geq 2$, we proved coarse thresholds for $k$-collapsibility for all $k$.
► CSPs and Compactness Principles
Anthony Li, Ishin Shah, Matthew Snodgrass, Rui Zhou
Advisor: Riley Thornton
Abstract: Constraint Satisfaction Problems (CSPs) are a well studied class of problems from computer science which come with a rich notion of complexity. Each CSP can be associated with a set theoretic compactness principle (a weak form of the axiom of choice). By studying the relative strengths of these compactness principles, one can obtain a partial (quasi) order on the difficulty of corresponding CSPs with some interesting connections to the algebraic and computational properties of CSPs.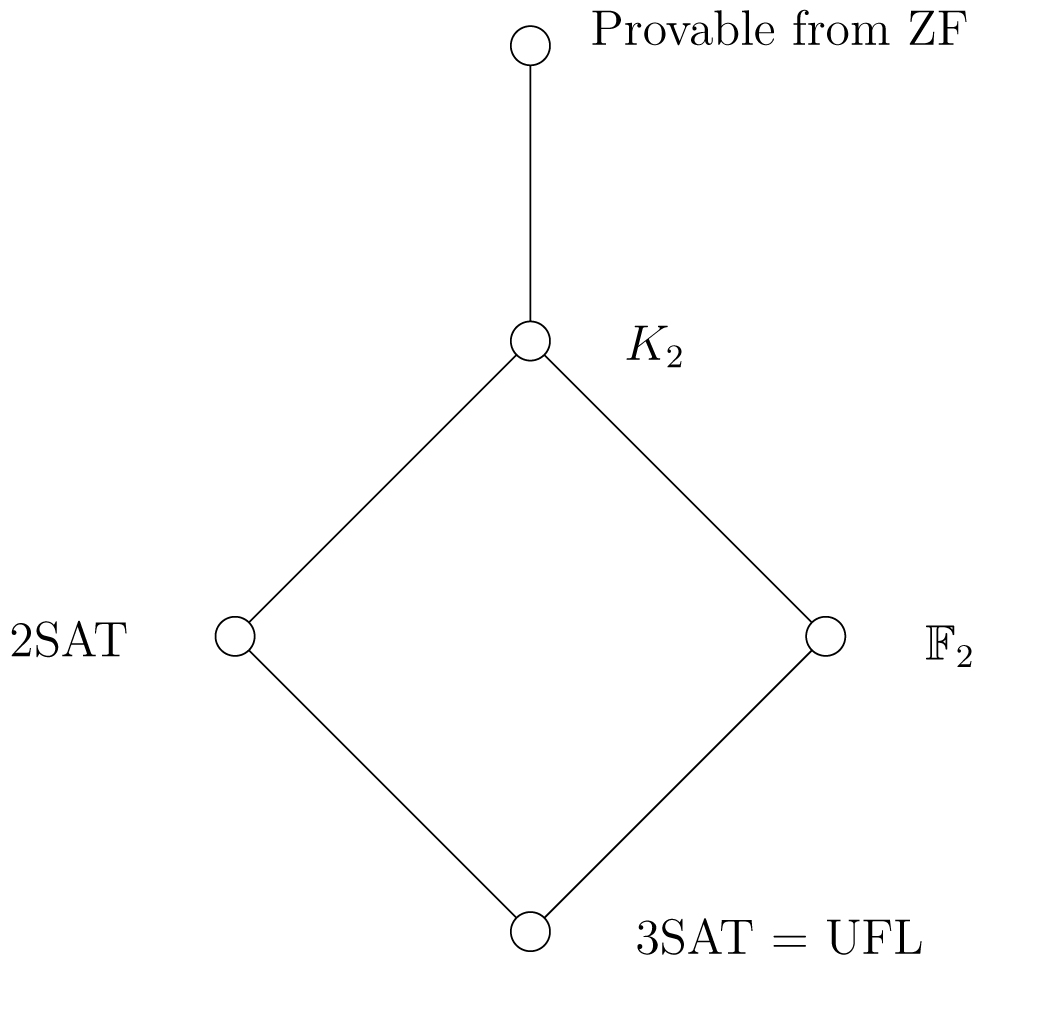
In this project we characterized those CSPs whose compactness principles are at the bottom of this order (those provable from ZF). We found an infinite sequence of compactness principles of increasing strength, corresponding to axioms of choice for larger and larger finite sets.
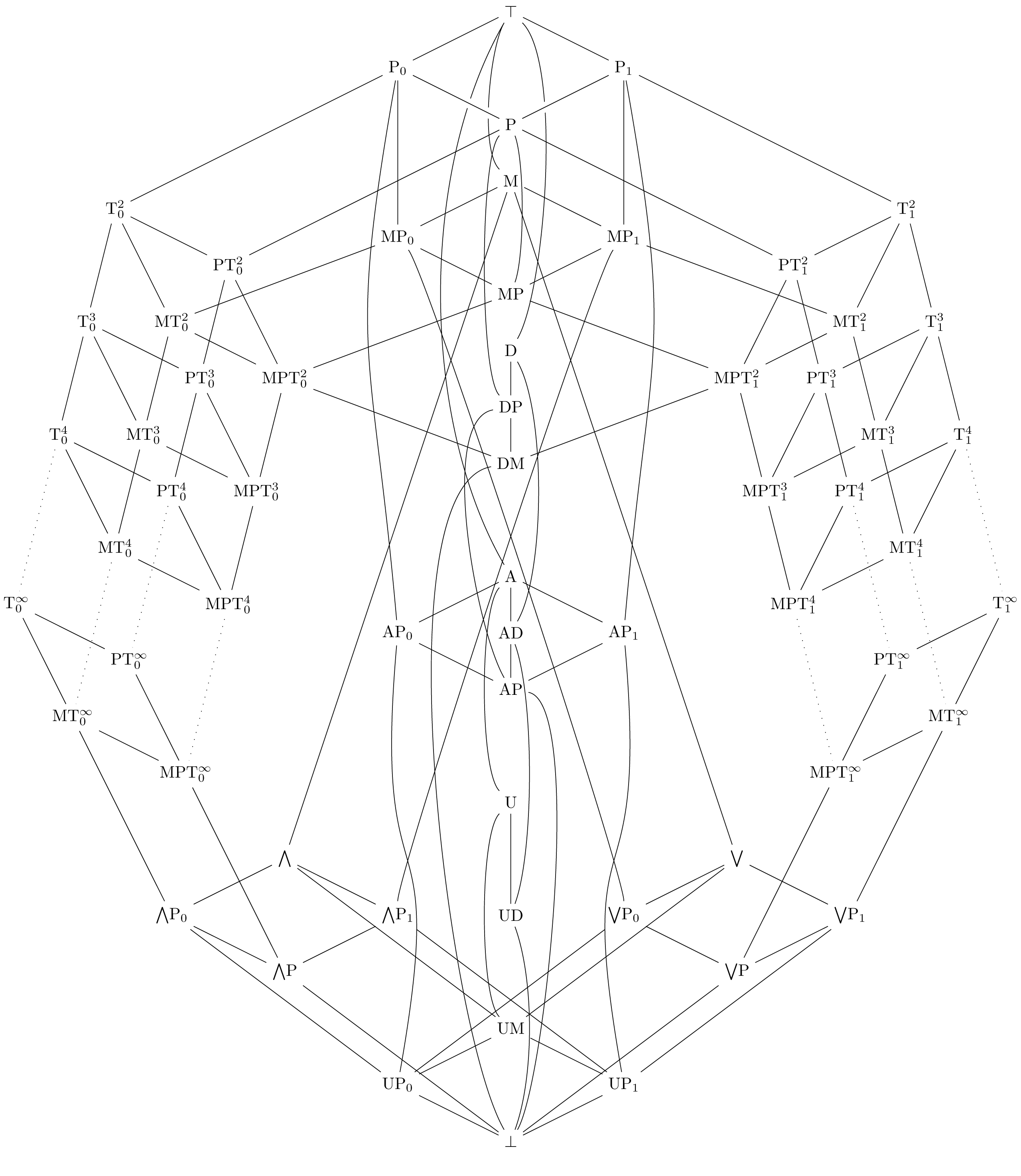
We found an infinite sequence of incomparable compactness principles. And, we separated out two intermediate classes of compactness principles for 2-valued CSPs, answering a question of Katya, Toth, and Vidnyanszky.
► Numerical Approximation of Degenerate Problems
Haozhan Ma, Daniel Zhou
Advisor: Noel Walkington
Abstract: Climate models need to simulate the release of dissolved as permafrost thaws, and the mathematical models of this process involve many "degenerate" equations. Algorithms for such problems frequently involve minimizing of convex functions that lack strict convexity and have low regularity. This project developed strategies to adaptively select step sizes as to be as large as possible for descent algorithms while still guaranteeing convergence.
► Embedding dimension gaps in sparse codes
Henry Siegel, David Staudinger, Yiqing Wang
Advisor: Amzi Jeffs
Abstract: We discuss the open and closed embedding dimensions of a convex code FP, derived from the Fano plane. We are motivated by the following question: do there exist convex codes whose open embedding dimension is large, but which have codewords of bounded size? The code FP has codewords of size at most three, and may be the first example of such a code whose embedding dimension is larger than 5. We explain that the closed dimension of FP is equal to 3, while the open dimension is either 4, 5, or 6. In particular, FP is the first example of a code whose codewords have size at most three, whose closed embedding dimension is three, and whose open dimension is not equal to closed dimension.
2023 SURF team
Students: Adam Bertelli, Brenda (Siran) Chen, Brandon Dong, Thomas Horstkamp, Benjamin Ingimarson, Iris Jiang, Yunseong Jung, Dhruv Kulshreshtha, Yoojung Christina Kwon, Subhasish Mukherjee
Faculty: Elisa Bellah, Boris Bukh, Giovanni Leoni, Alan Lew, Robin Neumayer, Aristotelis Panagiotopoulos, Bob Pego, Ian Tice, Tomasz Tkocz
2023 SEMS research team
Students: Maxim Grebinskiy, Anthony Li, Haozhan Ma, Ishin Shah, Henry Siegel, Matthew Snodgrass, David Staudinger, Yiqing Wang, Sophia Yang, Maolinsheng (Iris) Ye, Daniel Zhou, Rui Zhou
Faculty: Amzi Jeffs, Andrew Newman, Riley Thornton, Noel Walkington