► Edge Density of Maximally Linkless Graphs
Max Aires
Advisor: Florian Frick
Abstract: A spatial graph consists of points in space (vertices) connected by non-intersecting curves (edges). Such a graph is called linked if it contains a non-trivial link, that is, two disjoint cycles that link one another in the sense that they cannot be moved to disjoint cycles in a 2-dimensional plane without crossing some of their edges. Graphs that can be embedded without non-trivial links share many properties with those that can be embedded in the plane, such as a simple forbidden minor characterization and a linear upper bound on the number of edges. However, while planar graphs on $n$ vertices can always be extended to a maximally planar graph with $3n-6$ edges, we show that no similar rule applies for linkless graphs.
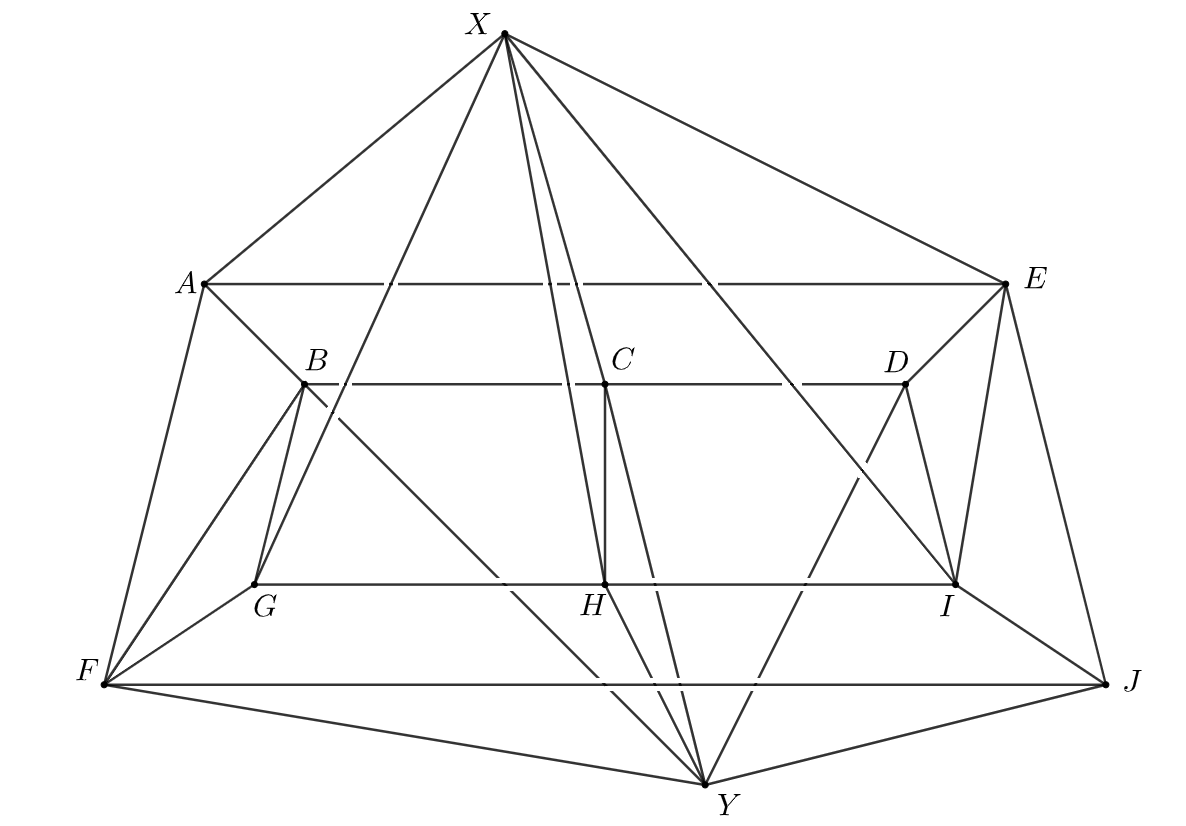
In particular, a result of Mader implies that a linkless graph with $n$ vertices has at most $4n-10$ edges, and this upper bound is optimal. However, we construct an infinite family of graphs on $n$ vertices and asymptotically less than $3n$ edges that are linkless, but adding any edge results in a non-trivial link.
► Finite Difference Scheme for Solving the Allen-Cahn Equation Coupled with an Elliptic Equation
Zhijie Chen
Advisor: Franziska Weber
Abstract: The project implements an algorithm (in MATLAB) for approximating a solution for Allen-Cahn equation coupled with an elliptic equation, a system of partial differential equations. This class of equations models the physical process of phase separation, and the elliptic equation introduces influences of an external field. Since we cannot hope to solve these partial differential equations analytically, we turn to numerical methods for a stable and accurate approximation. We turned the small but complex partial differential equation into a large but straightforward linear system (which a computer can easily solve). The algorithm was implemented for the equation with inhomogeneous Neumann boundary conditions.
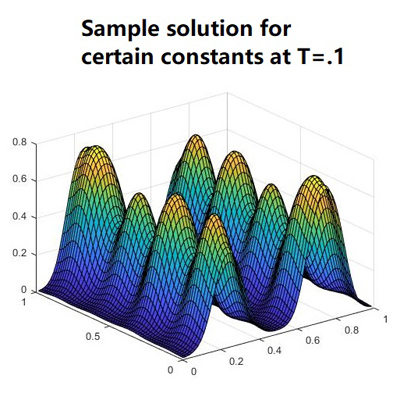
A first order accurate splitting scheme was implemented, which splits the Allen-Cahn equation into a diffusion and a reaction part, as well as multiple source terms, and each part is solved separately, which drastically reduces the complexity and also improves the speed of the algorithm. However, it was proved that the combined result still gives an accurate approximation of the original equation.
► Numerical Analysis of Liquid Crystals
Varun Gudibanda
Advisor: Franziska Weber
Abstract: Liquid crystals are an intermediate state between a liquid and a crystal. In a liquid, all the particles are randomly oriented while in a solid all the particles are completely aligned. In liquid crystals, we can think of the particles as being “vaguely oriented” in that if we look at a small section of a splotch of liquid crystals, they will all seem to be generally pointing in the same direction. Physicists have produced a system of partial differential equations (PDEs) that models a system of liquid crystals and predicts their alignment in space and time. These equations are very nonlinear and thus finding exact solutions is nearly impossible. We set out to produce a numerical scheme for this system of PDEs - that is, we wanted to produce an algorithm that would approximate solutions to this system of equations.
We found a fully-discrete scheme for this set of equations that was energy stable. In other words, we found a scheme that approximated the solution of the equations at specific discrete points in space and time that altogether obeyed an inherent energy law of the system. With this, we were able to simulate the system computationally and produce animations of the liquid crystals.

► 1D Free Boundary Problems
Scott Harvey-Arnold
Advisor: Giovanni Leoni
Abstract: In this research, we studied the existence and uniqueness of solutions to certain 1-dimensional free boundary problems. In these problems, we aim to minimize the integral of a given functional, but integrating only over the region where the inputted function is positive.
The work primarily used variational techniques in combination with standard minimization techniques to study these problems. We were able to give necessary and sufficient conditions for the existence of minimizers for a certain family of functionals, and proved uniqueness of solutions when they exist. We qualitatively studied these minimizers in order to understand when the set $\{u > 0\}$ is connected, where $u$ is the solution to a particular free boundary problem.
► New upper bound on extremal number for even cycles
Zhiyang He
Advisor: Boris Bukh
Abstract: In this project we study the maximum number of edges that a graph without a cycle of length $2k$ could contain. By developing methods used by Bukh and Jiang, we improve the upper bound on $\operatorname{ex}(n, C_{2k})$ by a factor of at least $\sqrt{\log k}$.
► Log-convexity of Moments of Averages
Philip Lamkin
Advisor: Tomasz Tkocz
Abstract: This project is devoted to moments of sums of independent and identically distributed nonnegative random variables. We consider the sequence of moments of arithmetic means of such random variables.
By the law of large numbers, this sequence converges to the expectation. We prove that the $p$-th moment is log-concave when $p < 1$ (including all negative values of $p$), and eventually log-convex when $p > 1$. We also conjecture that the sequence is always log-convex for $p > 1$. In addition, we give a partial characterization of the log-convexity/concavity for the non-normalized sequence.
► Multilevel Monte Carlo
Yile Liu
Advisor: Yu Gu
Abstract: Monte Carlo simulation (MC) of a random process is a useful numerical technique in science, engineering, and finance. It can be applied to job scheduling, mathematical optimization, financial options pricing, etc. MC method relies on repeated random samplings and its convergence rate is limited by the Central Limit Theorem to the order of the reciprocal of the square root of the sample size, which is not satisfactory in some real-world application. Currently, most of the efforts in speeding up the MC algorithms are spent on the so-called variance reduction. In this project, we study a method called the Multilevel Monte Carlo (MLMC) which can reduce the computational cost of standard Monte Carlo methods by taking most samples with low accuracy and corresponding low cost, and only very few samples are taken at high accuracy and corresponding high cost.
Besides the applications in finance, we apply MLMC to random differential equations which arise from exploration geophysics and materials design, and observe significant improvements of the convergence rate.
► Learning Transport Velocity Fields from Data
Hannah Milano
Advisor: Hayden Schaeffer
Abstract: Given an initial and final distribution, we would like to learn the velocity field that governs the flow map. The flow is modeled by a time-dependent transport equation with unknown velocity and unknown external forces. To discover the unknowns, we optimize the least squares error over all possible transport paths between the input/output data. The gradient is computed using the back propagation algorithm applied to an implicit Euler discretization of the transport system and the problem is optimized by a 2nd order solver.

Additionally, we extended the algorithm to the incompressible Navier-Stokes equation in 2D with external forces.
► What can you draw?
Fei Peng
Advisor: Florian Frick
Abstract: We introduce a notion of drawability in the plane; intuitively a set in the plane is drawable if it can be obtained by successively drawing a collection of unit disks, then erasing some collection of unit disks, then drawing again, and so on.
A surprising property is that not every shape whose boundary has small curvature is drawable. One such example is illustrated.

► Inequalities in Convex Geometry
Matthew Shi
Advisor: Raghavendra Venkatraman
Abstract: In this project we studied multiplicative inequalities in convex geometry, taking inspiration from the recent progress on the Gaussian correlation inequality by Royen, via the lens of the more familiar Brunn-Minkowski theory for convex sets. The latter asserts that for any measurable sets $A$ and $B$ in $n$ dimensions the Lebesgue measures of $A, B$ and the Minkowski sum $A+B$ are related by $\mu(A+B)^{1/n} \geqslant \mu(A)^{1/n} + \mu(B)^{1/n}$, while the former asserts that for any pair of convex bodies $E$ and$ F$, their Gaussian measures satisfy the inequality $\rho(E \cap F) \geqslant \rho(E) \rho(F)$, for any Gaussian measure $\rho$ on $\mathbb{R}^n$.
The goal of this project was to characterize all additive and multplicative inequalities of the form $f(|E|) + f(|F|) \leqslant f(|E+F|) + f(|E \cap F)|$, where $|\cdot|$ denotes either Lebesgue or Gaussian measure and $E$ and $F$ are convex bodies in Euclidean space. We proved that $f(t) = t^r$ is such a function for the Lebesgue measure provided $r \geqslant 1$. More generally, we showed that such an inequality for any increasing convex function $f$. We used a library of functions called \textit{lrslib} to conduct numerical experiments on polytopes to check the validity of some further conjectures regarding the class of all functions $f$ for which such an inequality holds.
► Minimizing curve and distribution of Average Network Commute Time problem
Xiang Si
Advisor: Dejan Slepčev
Abstract: In this project, we study a non-convex optimization problem that combines optimal transportation network planning and shape optimization. Specifically, we try to determine the pair of transport network and distribution of agents such that the total cost is minimized. The cost function penalizes the length of the network, the total travel distance between pairs of agents and the density of the agent packing. The cost of traveling along the network is set to be traveling outside the network. We investigate the properties of such minimizing pairs and propose an iterative numerical approximation algorithm using Wasserstein gradient flow and Multiple Penalized Principal Curve algorithms to approximate the optimal solution.
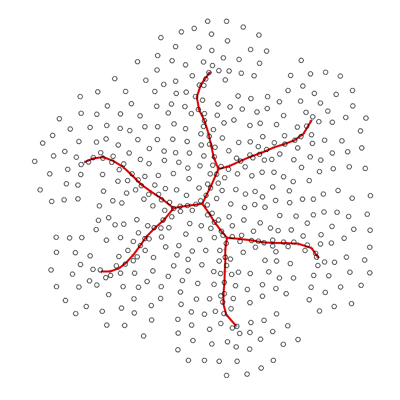
We also performed experiments in 2-d settings with different initialization of network structure.
► Steady-State Stability Analysis of Periodic Micropolar Fluids
Noah Stevenson
Advisor: Ian Tice
Abstract: We consider the system of partial differential equations which encode the physics of an incompressible micropolar fluid with spherical mircostructure residing in the three dimensional flat torus. We are primarily concerned with the time evolution of two vector fields: the linear velocity field and the intrinsic angular velocity field. We pose the question: in the absence of forcing, what `steady-state' angular velocity fields solve the spherical micropolar equations with zero linear velocity? It turns out that there is a large family of these steady-state solutions which solve a simple parabolic partial differential equation with conservative data. Given one of these steady-states we then analyze the stability of nearby solutions to the incompressible and spherical micropolar fluid equations. We study the linearization around the steady-state and prove a functional-analytic well-posedness result.
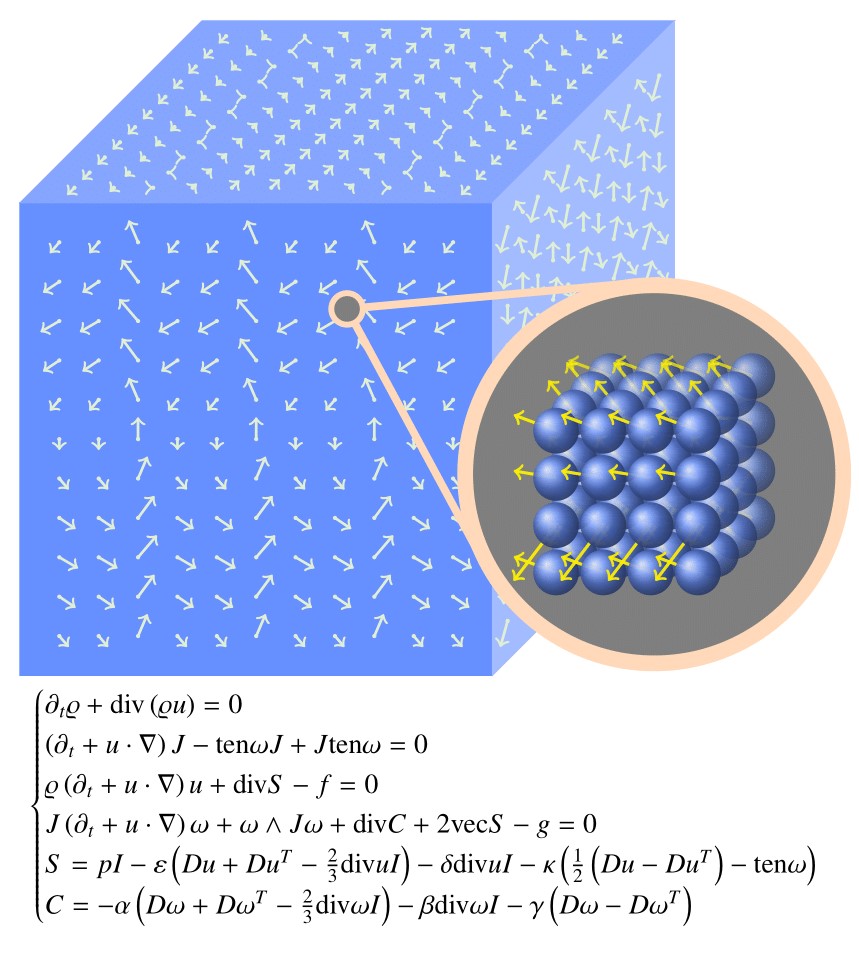
This linear result is strong enough to allow one to solve the nonlinear micropolar equations in perturbation form for small data and small forcing. We then find that such solutions are both stable and attractive.
► Horizontal-Vertical Geometry for Signal Comparison
Jianming Wang
Advisor: Dejan Slepčev
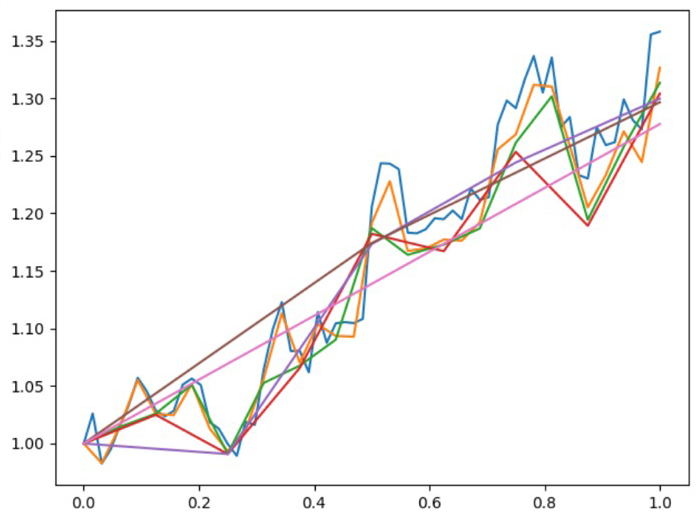
Abstract: The goal of this project is to develop and study a new geometry for comparing 1D signals (functions). Signals are often considered `close' if they exhibit similar patterns which are close in space and intensity. Thus a geometry for signals should allow for both intensity and spatial deformations. Present notions of signal geometries do not achieve that. We introduce a new Reimannian metric on the space of signals that is better aligned with the intuition. We set up a functional which is minimized by the geodesics in this space and investigated its properties.
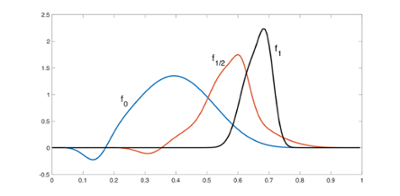
Furthermore this project introduced a numerical scheme for computing the approximate geodesics. In the picture below we display the midpoint of the geodesic $f_{1/2}$ connecting signals $f_0$ and $f_1$, which can thus be considered as the average of signals $f_0$ and $f_1$ in the space of signals introduced.
► An estimator of point/manifold-manifold distance based on local PCA
Yuepeng Yang
Advisor: Dejan Slepčev
Abstract: Some high-dimensional data sets have low-dimensional manifold structure and it is relevant to estimate point to manifold and manifold to manifold distance given n data points sampled from an m-dimensional manifold. We proposed a computationally efficient estimator based on tangent plane estimation using principal component analysis in a local neighborhood. Error bounds are derived for noise-free and noisy conditions.
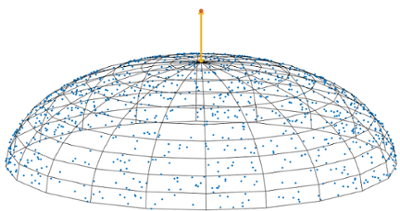
In the noise-free setting, an estimator based on nearest points would give an error bound of $O(n^{-1/m})$ while our estimator reduces it to $O((n/ \log {n})^{-2/m})$.

