CMU Mathematics Undergraduate Research, 2022

In early 2020, as the global coronavirus pandemic brought the world to a screeching halt, many of our students found that their summer programs had been cancelled. Many of these students were very interested in using this suddenly free summer to engage with open ended-projects in mathematics. In response to this demand, the Department of Mathematical Sciences curated a brand new summer program: Summer Experiences in Mathematical Sciences (SEMS). This program is offered in parallel with the traditional SURF program, which provides stipends to students who stay at CMU in the summer months to work on research projects. Find below details of the projects conducted in the summer of 2022 under the auspices of the SURF and SEMS program.
▼ SURF projects
► Chessboard cutting in high dimensions
Alexander Brick
Advisor: Tomasz Tkocz
Abstract: It is folklore that a line can meet the interiors of no more than $2N − 1$ squares of the usual $N \times N$ chessboard and this bound is tight. Recently Barany and Frenkel have derived an analogous asymptotic expression for slicing $n$- dimensional convex bodies by hyperplanes, up to a constant factor, which has then been found by Aliev, in the case of the cube. We generalise Aliev's result from the cube to all 1-symmetric convex sets (symmetric with respect to the coordinate hyperplanes and the permutations of the axes).
► Limit Cycle Oscillations and Instabilities in Bridge Dynamics
Rachel Dolle
Advisors: Jason Howell and Justin Webster (UMBC)
Abstract: In this research we develop codes to construct computational simulations of the dynamics of a structure immersed in a surrounding flow field. The dynamics of the structure are modeled by a nonlinear fourth-order partial differential equation (PDE) with implicit damping terms and a piston-theoretic term representing the fluid-structure interaction. The configuration of interest is that of a long, slender beam that is hinged on two opposing ends and is free on the two long sides, modeling the behavior of a suspension bridge. The project resulted in both finite difference codes and spectral method codes to simulate the dynamics of the bridge.
The purpose of the project is then to study the dynamics of the bridge configuration under certain conditions. Of particular interest in this work is the examination of parameter regimes that lead to flutter, a sustained dynamic instability that could lead to structural issues.
The work also focused on the composition of Limit Cycle Oscillations (LCOs) that may arise in the flutter regime.
The animation depicts an interesting case where the flutter behavior is, at the onset, seemingly dominated by torsional mode instabilities with large magnitudes. However, at around 25 seconds into the simulation, the flutter transitions to a state where longitudinal mode instabilities begin to dominate and absorb the energy from the torsional oscillations.
► Stability of the polydisc slicing
Nathaniel Glover
Advisor: Tomasz Tkocz
Abstract: The $n$-polydisc is the n-Cartesian product of the unit disc in the complex plane. Building on recent results in the real case for the cube, we study the stability result for the maximal volume cross-sections of the $n$-polydisc by complex hyperplanes.
► Steinhaus-Gaussian tail comparison
Xinjie He
Advisor: Tomasz Tkocz
Abstract: We aim to establish a sharp Gaussian tail bound for weighted sums of independent Steinhaus random variables (uniform on the unit circle in the complex plane). En route, we need to develop basic tools such as Berry-Esseen type bounds for complex valued, rotationally invariant random variables, previously known only for realvalued random variables.
► A new data-driven reduced order model for parabolic inverse source problems
Ricky (Yuxuan) Huang
Advisor: Yangwen Zhang
Abstract: In this paper, we propose a new data-driven reduced order model for solving parabolic inverse source problems.
We prove that our new method can be orders of magnitude faster than standard solvers, and is also much less memory intensive. Numerical experiments are presented to confirm our findings.
► Boundary Conditions on the Second-Order Singularly-Perturbed Problem on $\mathbb{R}$
Thomas Lam
Advisor: Giovanni Leoni
Abstract: The Second-Order Singularly-Perturbed Problem concerns the integral functional $\int_\Omega \epsilon_n^{-1}W(u) + \epsilon_n^3\|\nabla^2u\|^2\,dx$ for a bounded open set $\Omega \subseteq R^N$, a sequence $\epsilon_n \to 0^+$ of positive reals, and a function $W:R \to [0,\infty)$ with exactly two distinct zeroes. This functional is of interest since it models the behavior of phase transitions, and its Gamma limit as $n \to \infty$ was studied by Fonseca and Mantegazza. In this paper, we study an instance of the problem for $N=1$. We find a different form for the Gamma limit, and study the Gamma limit under the addition of boundary data.
► New cycle decompositions of even hypercubes
Idael Martinez-Perez
Advisor: David Offner
Abstract: We say a graph $H$ decomposes a graph $G$ if the edges of $G$ can be partitioned into copies of $H$. The $n$-dimensional hypercube $Q_n$ is the graph that has vertex set ${0,1}^n$ and with edges connecting the vertices that differ in exactly one coordinate.
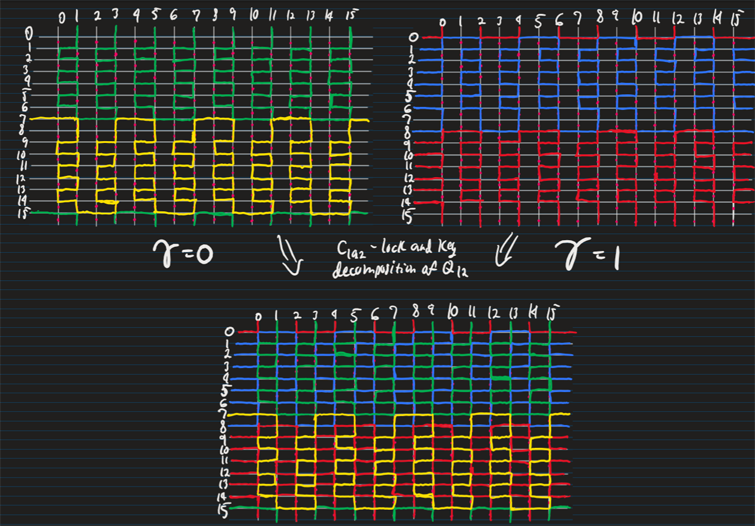
This research focuses on decomposing hypercubes of even dimension into cycles. Research in this area goes back to Ringel, who proved that if $n$ is a power of 2, then $Q_n$ can be decomposed into Hamiltonian cycles, and subsequently Aubert and Schneider proved that all even hypercubes can be decomposed into Hamiltonian cycles.
Further research has focused on decomposing hypercubes into short cycles (Horak, Siran, and Wallis; Waphhare, Borse, and Tapadia), cycles whose length is a power of 2 (Offner and Gibson) and long cycles (Axenovich, Offner, and Tompkins), but the general question of which cycles decompose the hypercube remains open. Building on the research of Axenovich, Offner, and Tompkins, we construct cycle decompositions of the hypercube for new cycle lengths. A key step in the constructions are novel cycle decompositions of Cartesian products of cycles.
► Logarithmic convexity of Rademacher averages
David Rotunno and Joseph Kalarickal
Advisor: Tomasz Tkocz
Abstract: We prove the logarithmic convexity of the p-norms of Rademacher (random sign) averages of exponential functions. Our approach relies on a new variational formula for the L_1-norm of Rademacher averages. This extends in a probabilistic way a recent result on the dual log-Brunn-Minkowski inequality for convex symmetric sets due to Saroglou.
► Trace of homogeneous fractional Sobolev spaces on strip-like domains
Khunpob Sereesuchart
Advisor: Giovanni Leoni
Abstract: In this project, we analyzed the trace operator for homogeneous fractional Sobolev spaces for infinite strip-like domains of Lipschitz continuous width. This extends the result from homogeneous fractional Sobolev spaces for strip domains of constant width from the previous summer.
Similar semi-norms were derived, which included both a close bound and a far bound; however, the techniques required to solve were more complex. Due to the space being potentially non-convex, unlike the constant width case, many directional methods previously used, such as moving indefinitely along the axes, could not be used. A directional approach was only used when comparing near points, where the axis perpendicular to the two sides of the strip and the axes parallel were split. Otherwise, the rest of the points were compared directly, leading to a more general approach to determining the trace of homogeneous fractional Sobolev spaces.
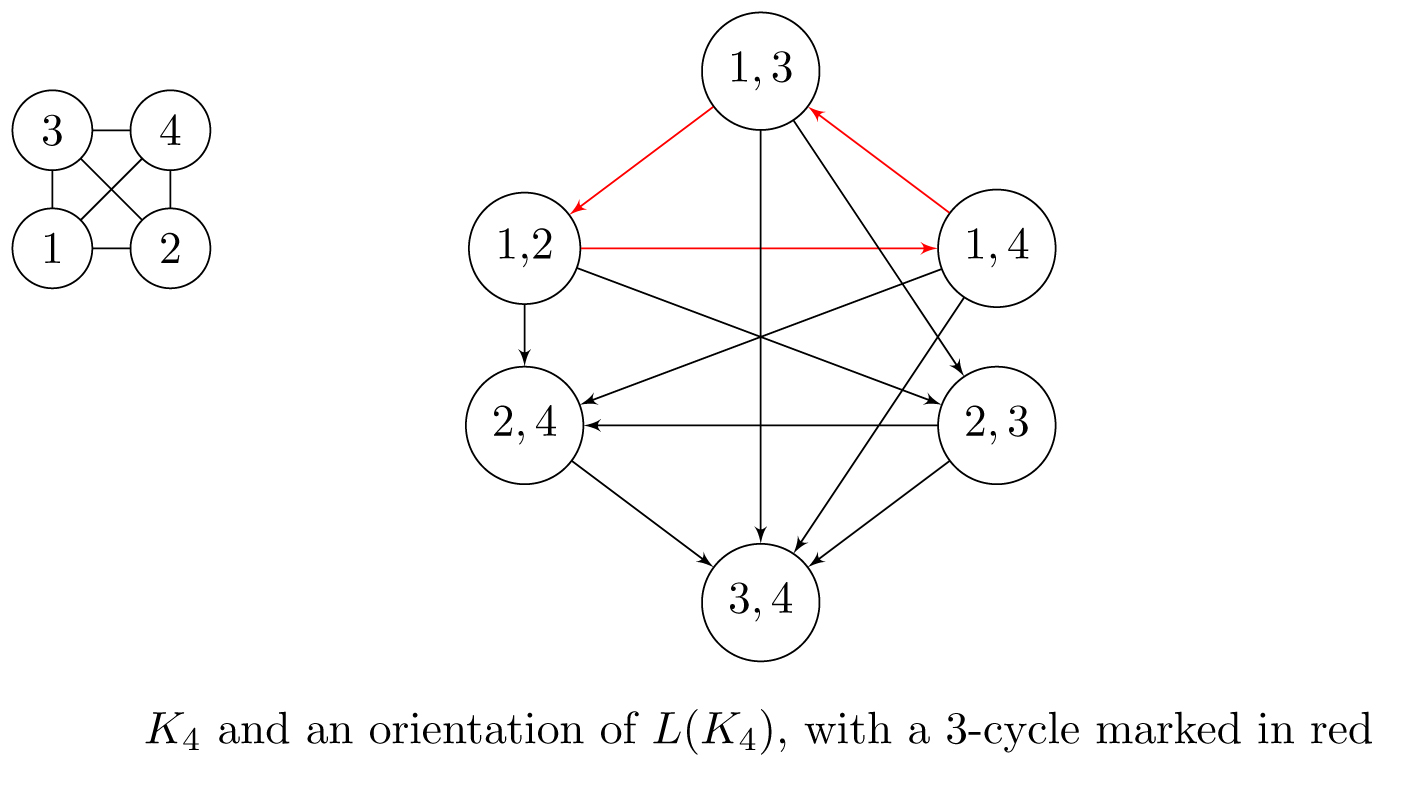
► On the enumeration of acyclic and 3-cycle-free orientations
Saadiq Shaikh
Advisor: Prasad Tetali
Abstract: We consider the problem of enumerating 3-cycle-free orientations (3CFOs) of an undirected graph. Inspired by a random sampling question of Dr. Richard Darling, we focused on the enumeration of 3CFOs of the line graph of $K_n$. A line graph $L(G)$ of a graph $G$ represents adjacencies between edges of $G$; every edge in $G$ is a vertex in $L(G)$, and two vertices in $L(G)$ are adjacent if their corresponding edges in $G$ share a vertex. Each vertex in $K_n$ has a corresponding clique in $L(K_n)$ of size $n-1$, which gives us some understanding of the 3-cycle-free orientations of $L(K_n)$. We obtain the following theorem: There exist absolute constants $$c_1 n^2 \le \log(3CFO(L(K_n))) \le c_2 n^2 \log n.$$
The proof of the lower bound is nontrivial, while the upper bound above is straightforward using known facts about tournaments. Going forward, making the above estimate asymptotically tight, as $n\to \infty$, is one of our next lines of investigation.
► An elementary approach to pointwise multiplication in Sobolev-Slobodeckij spaces
Kevin You
Advisor: Giovanni Leoni
Abstract: Sobolev spaces, as an important tool in partial differential equations, have been built on techniques of functional and harmonic analysis. More recently, efforts are being made to reconstruct theories of Sobolev spaces with the Gagliardo semi-norm and only basic theories of integration. In this project, we derive necessary and sufficient conditions for pointwise multiplication of fractional Sobolev-Slobodeckij spaces in one dimension by using classical embedding of Sobolev and Besov spaces along with elementary inequality bounding and stress-testing techniques.
▼ SEMS projects
► Realizing convex codes with axis-parallel boxes
Miguel Benitez, Brenda Chen, Tiffany Han, Kina Paguyo and Kaz Zhou
Advisor: Amzi Jeffs
Abstract: Every collection of sets in Euclidean space can be associated to a combinatorial code, which records the regions cut out by the sets in space. We prove a general "product theorem" for codes, characterizing the effect of taking pairwise products of sets from two collections on the code realized by the collections. We use this theorem to characterize the codes realizable by axis-parallel boxes, and to exhibit differences between this class of codes and those realizable by convex open or closed sets.
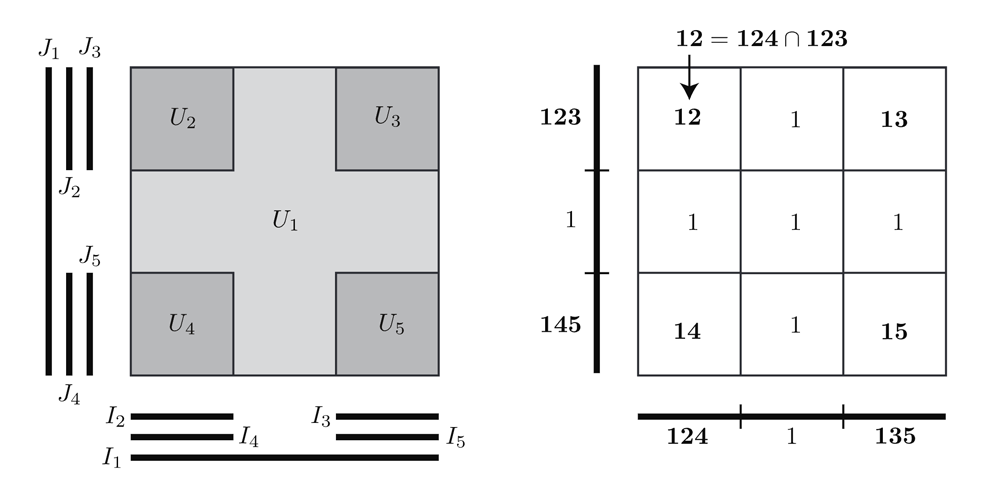
We also use our theorem to prove that a "monotonicity of open convexity" result of Cruz, Giusti, Itskov, and Kronholm holds for closed sets when some assumptions are slightly weakened.
► Expected length of a War-like card game
Adam Bertelli
Advisors: Boris Bukh and Zichao Dong
Abstract: Consider a simplified version of the card game War: a deck of n cards, labelled 1 through n, is split among two hands. At each turn, both players draw a card uniformly at random from their hand, and whoever drew the lower rank card adds both drawn cards to their hand.
How long (in expectation) will it take before one player holds all the cards?
We can model this game as a Markov process with a terminating state. By using various coupling arguments and associated Poisson point processes, we demonstrate many nice properties of this model. These properties allow us to derive an exact recursive form for the expected number of steps until the terminating state is reached, along with several asymptotic bounds on this value.
► Near-top dimension homology in multi-parameter simplicial complexes
Connor Gordon, Xinyi (Erica) Wang, Xinyu (Alex) Cui
Advisor: Andrew Newman
Abstract: We covered the fundamentals of homology of simplicial complexes. We then overviewed the standard random models, both the combinatorial models (Linial--Meshulam--Wallach, Kahle's random clique complex, and the Costa--Farber multiparameter model) and the geometric models (Čech and Vietoris--Rips complexes of random point sets). We particularly focused on how graph threshold questions generalize to homology vanishing and non-vanishing thresholds for random spaces. From here we established new, non-vanishing homology statements in the multiparameter model.
► Unbalanced Unimodal and $k$-Modal Subsequences
Ethan Gu, Charles Gong, Zhehan Yu and Ziqi Yang
Advisors: Boris Bukh and Zichao Dong
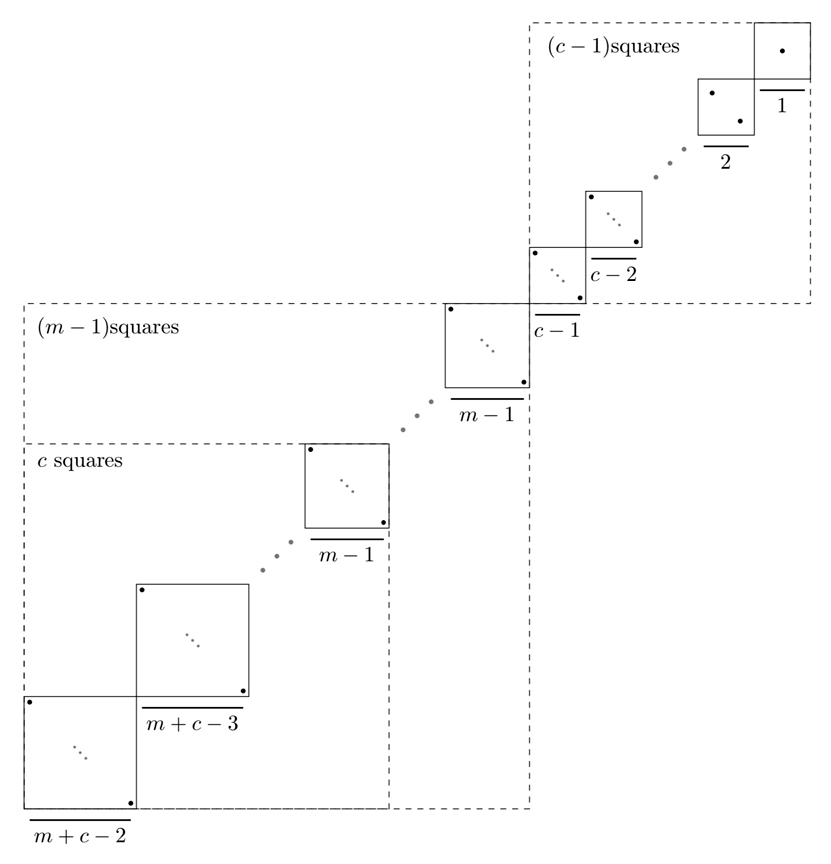
Abstract: In 1935 Erdős and Szekeres proved that every sequence of $n$ distinct numbers contains a monotone (i.e. increasing or decreasing) subsequence of length at least $\sqrt{n}$. In 1979, Chung proved that every sequence of $n$ distinct numbers contains a unimodal (i.e. increasing then decreasing or decreasing then increasing) subsequence of at least length $\sqrt{3n}$. In this paper we consider $k$-modal (a subsequence with k "zig-zags") subsequences and unbalanced unimodal subsequences. In particular, we proved that every sequence of $n$ distinct numbers contains an increasing $k$-modal subsequence of length at least $\sqrt{2nk}$, and that every sequence of length $(m-1)^2 + c(c-1) + 1$ contains an increasing unimodal subsequence with either its increasing part longer than or equal to $m$ and its decreasing part longer than or equal to $c$ or vice versa. We also showed these bounds were sharp.
► Projective amalgamation for connected planar graphs
Tianwei (Owen) Li, Veda Vaishnaavi Vakkada, Ziyun (Zoey) Liu
Advisors: Aristotelis Panagiotopoulos and Felix Weilacher
Abstract: A category $\mathcal{C}$ of finite graphs has the $\bf {Projective Amalgamation Property}$ (PAP) if for every two maps $ f : B \to A$ and $ g : C \to A$ in $\mathcal{C}$, there are $ f' : D \to B$ and $ g' : D \to C$ in $\mathcal{C}$, so that $f\circ f' = g\circ g'$. This property has been extensively used in recent years for showing that several topological spaces with interesting properties can be viewed as the "generic" objects which are approximable from natural families of finite graphs.


For example, a recent result of Panagiotopoulos-Solecki shows that the category $\mathcal{G}$ of all finite connected graphs with connected epimorphisms satisfies PAP and the associated generic object is a continuum known as the universal Menger curve.
The main goal of this project was to extend these ideas in the planar context. In particular, we considerer the category $\mathcal{P}$ of all finite connected $\bf {planar}$ graphs with connected epimorphisms. We showed that the class $\mathcal{P}$ satisfies PAP, and hence it canonically approximates the planar version of the Menger curve, known as the Sieprinski carpet.
► Rearrangements of functions
Braden Yates and Jiewen Hu
Advisor: Giovanni Leoni
Abstract: Given measurable $f: R^n \rightarrow R$, a rearrangement of $f$ is any function from $R^n$ to $R$ with an identical distribution function. The spherically decreasing rearrangement of $f$ is often studied due to its preservation of characteristics of the parent function; examples are inclusion in $C_c(R^n; R)$ and the $\mathcal{L}_1$ measure of the gradient. In this project, we restrict to functions from $R$ to $R$ and establish preservation of bounded variation in two ways. We also present a generalization of the second method to show preservation of absolute continuity.
2022 SURF team
Students: Alexander Brick, Rachel Dolle, Nathaniel Glover, Xinjie He, Ricky (Yuxuan) Huang, Joseph Kalarickal, Thomas Lam, Idael Martinez-Perez, David Rotunno, Khunpob Sereesuchart, Saadiq Shaikh, Kevin You
Faculty: Jason Howell, Giovanni Leoni, David Offner, Prasad Tetali, Tomasz Tkocz, Justin Webster (UMBC), Yangwen Zhang
2022 SEMS research team
Students: Miguel Benitez, Adam Bertelli, Brenda Chen, Xinyu (Alex) Cui, Charles Gong, Connor Gordon, Ethan Gu, Tiffany Han, Jiewen Hu, Tianwei (Owen) Li, Ziyun (Zoey) Liu, Kina Paguyo, Veda Vaishnaavi Vakkada, Xinyi (Erica) Wang, Ziqi Yang, Braden Yates, Zhehan Yu, Kaz Zhou
Faculty: Boris Bukh, Zichao Dong, Amzi Jeffs, Giovanni Leoni, Andrew Newman, Aristotelis Panagiotopoulos, Felix Weilacher