► Asymptotic stability of the Faraday wave problem
David Altizio, Xinyu Wu, Taisuke Yasuda
Advisor: Ian Tice
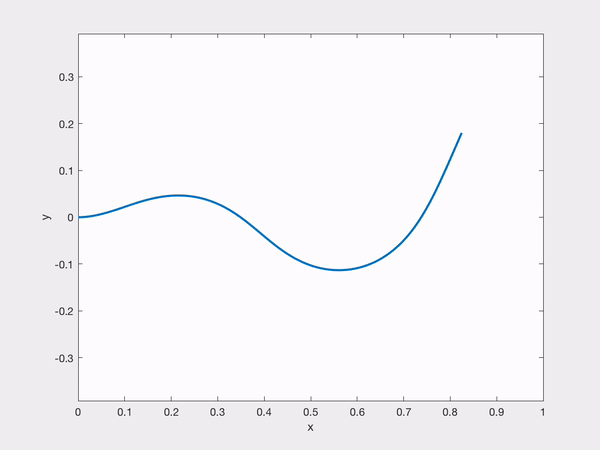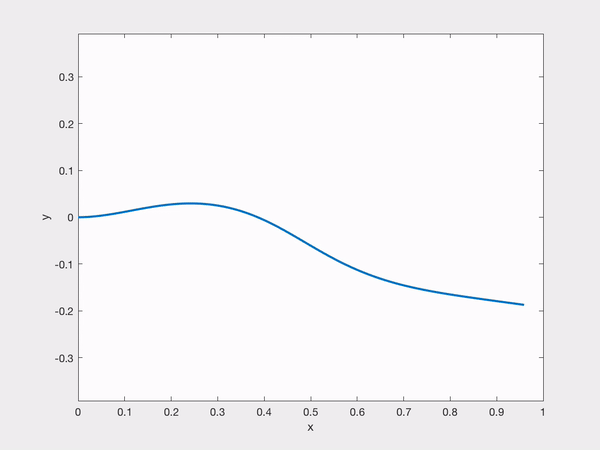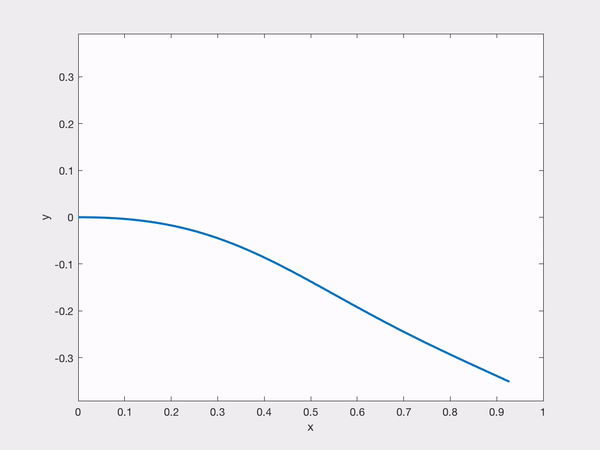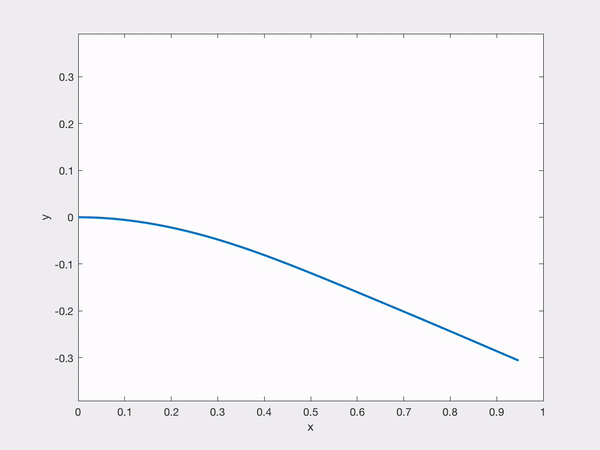
Abstract: This project concerns the dynamics of Faraday waves, a layer of incompressible viscous fluid lying above a vertically oscillating rigid plane with an upper boundary given by a free surface. We consider the problem with gravity and both with and without surface tension for horizontally periodic flows. This problem gives rise to steadily oscillating solutions, and the main thrust of this project is to study the asymptotic stability of these solutions in certain parameters regimes. More specifically, we prove that there exists a parameter regime of the amplitude and frequency of the oscillation in which sufficiently small perturbations of the equilibrium at time $t = 0$
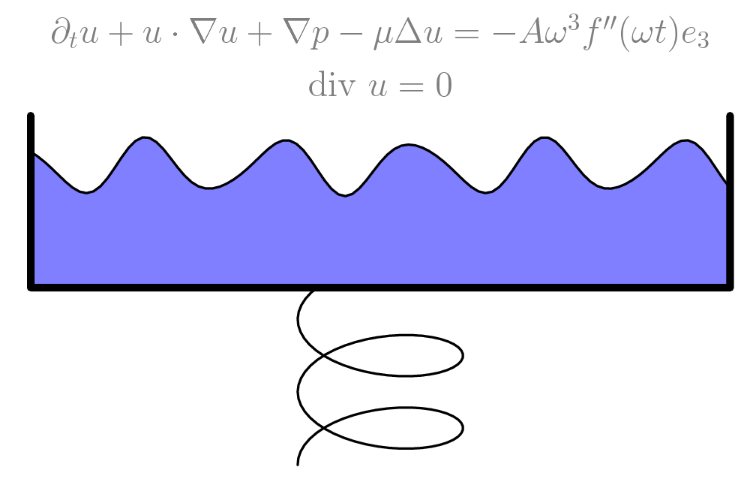
give rise to global-in-time solutions that return to equilibrium exponentially quickly in the case of fixed surface tension and almost exponentially in the case of vanishing surface tension.
► Constructing Local Volatility Surfaces to Price Options
Bryan Ding, Zilin Wang
Advisor: Elnur Emrah
Abstract: The Black-Scholes formula provided, for the first time, a theoretical method of fairly pricing a risk-hedging security. It gives the theoretical value of a European option in terms of the strike price and time to the expiration of the option, the interest rate in the money market, and the current price and volatility of the underlying stock. The volatility measures how risky the stock is. The implied volatility is defined to be the value of the volatility for which the value of an option given by the Black-Scholes formula agrees with the actual market value of the option. Under the classical Black-Scholes assumption, the volatility of an option should remain constant over its life; however, if one plots the implied volatility of an option against its strike price, one sees that the graph actually resembles a U-shaped curve that slopes upwards on both ends.
This phenomenon is known as the volatility smile. By plotting both the implied volatilities for Amazon stocks obtained from Bloomberg and the implied volatilities obtained from the Black-Scholes formula against the strike prices, similar behaviors of the graphs were observed. This ensured that the implied volatilities obtained from the Black-Scholes formula are good predictors of market volatilities. From there, local volatility surfaces were constructed. The local volatility surface is the graph of market volatility as a function of the time to maturity and the strike price of an option. By considering a simple parametrization of the local volatility function given by $\sigma(S,T)=(aS+b)^2+(cT+d)^2+e$, different sets of parameters $(a,b,c,d,e)$ were tested in Mathematica to determine the parameter with the smallest sum of squared error compared to market prices. This choice of the local volatility function is then used to approximate option prices when solving the Black-Scholes Partial Differential Equation.
► Does Gaussian noise increase entropy?
Wenxin Ding
Advisor: Tomasz Tkocz
Abstract: The (differential) entropy $S(X)$ of a continuous random variable $X$ with density $f$ is the integral of $-f \log {f}$. It is well known that the entropy of a random variable is never greater than the entropy of a Gaussian random variable with the same variance. This research focuses on analogues of this for sums of independent random variables. Is it true that for independent random variables $X$ and $Y$, $S(X+Y)$ is less than or equal to $S(X+G)$ or $S(G+Y)$, where $G$ is an independent Gaussian with the same variance as $X$ or $Y$ respectively?
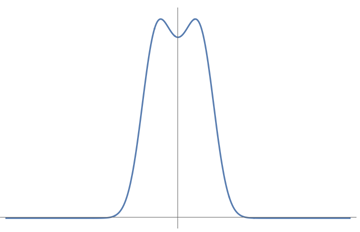
We find examples showing that in general the answer is "no" (our construction gives symmetric $X$ and $Y$ with the same variance and densities as shown in the picture). We conjecture that the answer is positive for identically distributed summands and look for natural classes of distributions supporting this.
► Assessment of Discrete and Continuous Time Models for Pricing Options
Shuyang (Serena) Gao, Novdano Dede Yusuf
Advisor: David Handron
Abstract: This research aims to assess four different option pricing models: Binomial, Black Scholes, Heston Stochastic Volatility and SABR, and find the most appropriate model for pricing options as well as examine the effect of different parameter values on the price produced by the models. This project brought together the knowledge of mathematical finance, probability, statistics and computer programming.
The main approaches to evaluate the models are by computing price under the different models for different options, calibrating the model by optimizing across the parameter space, and comparing the result with market data to see which model produces minimum error when matching market data.
After the evaluation of those models, we simulated delta hedging under those models and investigated their performances in terms of profit and loss.
► Dynamics of the Inextensible Inverted Flag with Piston-Theoretic Forcing Term
Varun Gudibanda
Advisor: Jason Howell
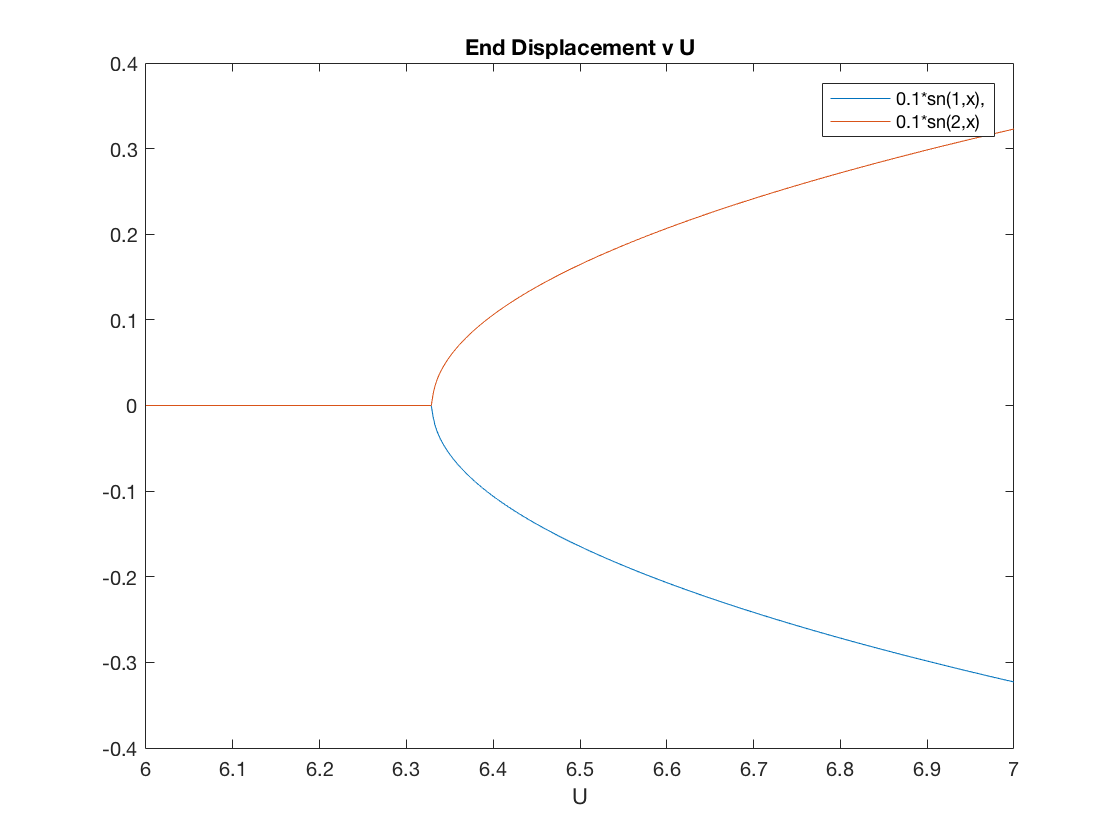
Abstract: In this research we examined the inextensible inverted flag system. In this system, a thin metal beam is fixed on one end and free to move on the other. Fluid such as water or air flows from the free end to the fixed end (inverted flag), inducing motion of the beam. This model is of current interest in several applications, including in the design of piezoelectric energy harvesting devices.
A full model of this system considers the movement of the beam and the movement of the fluid separately with a coupling term that describes the interaction between the fluid and the beam. Furthermore, the beam is assumed to be inextensible (i.e., of a constant length), which introduces nonlinearities in the PDE model. This results in a system of partial differential equations (PDEs) that is computationally expensive and analytically difficult to investigate. Engineers who have looked at this system make simplifying assumptions on the interaction between the fluid and the beam using tools from Piston Theory, resulting in a single PDE.
► Hidden Markov Model and its applications to stock price prediction
Yong Gun Choe
Advisor: Yu Gu
Abstract: It is common for professional investors and even the average investor to use different types of tools such as technical analysis to determine the price of a stock in the future. While there are no certain guarantees, people have come up with different ways to “predict” various future stock prices. So for this research, we introduce a famous method called Hidden Markov Model (HMM), a statistical signal prediction model, to predict stock prices based on previous prices. There are three important steps to understanding the HMM. The first step is to realize that a stock price changes with time but we do not know if it is going to go up or down. This is a Markov process but we are unable to directly observe this, hence being a hidden state.
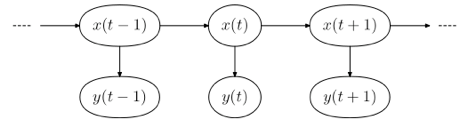
The second step is to observe something that is correlated with the changing of the stock price. For example, we can focus on the today’s closing, highest and lowest price to predict tomorrow’s closing price. We then have to come up with an emission probability that links such factors to the price of the stock. The third step is to figure out the transitional probability of a stock price changing from one specific time to the next. By carrying out various models depending on the situation of the market, we can see that HMM is a powerful tool for modeling stock returns.
► Hypergraphs with few Berge paths of fixed length between vertices
Zhiyang He
Advisor: Michael Tait
Abstract: In this project we studied the maximum number of hyperedges which may be in an $r$-uniform hypergraph under the restriction that no pair of vertices has more than $t$ Berge paths of length $k$ between them. When $r=t=2$, this is the even-cycle problem asking for $\mathrm{ex}(n, C_{2k})$. We extend results of Füredi and Simonovits and of Conlon, who studied the problem when $r= 2$.
In particular, we show that for fixed $k$ and $r$, there is a constant $t$ such that the maximum number of edges can be determined in order of magnitude.
► Recognizing Mesh Structure in Images
Ruoyuan Liu, Yuepeng Yang
Advisor: Dejan Slepčev
Abstract: In this project we developed methods for an image processing problem: recognizing mesh structures in images. Given a set of grayscale images representing the slices of a sample (imaged by a confocal microscope) the task is to precisely reconstruct the deformed mesh. The difficulties of this task lie in the fact that the deformations can be large, the noise is substantial, and the mesh can be damaged at places. We introduced a robust method that is able reconstruct the deformed mesh for a broad collection of image sets. After some low level image processing, we apply landmark detection (represent each cell with a single vertex) and elastic surface registration.
The elastic mesh registration rewards agreement with the detected landmarks and the smoothness of the mesh. In order to reliably recover the precise mesh structure we developed a randomized algorithm that starts with small patches and progressively builds and completes large meshes. In addition, we were able to build time series alignment to track the change of the mesh structure over time.

► Line sections and graph homomorphisms for graphs induced by actions of the integer lattice
Jung Joo Suh
Advisor: Clinton Conley
Abstract: Many traditional graph-theoretic problems, like the existence of proper colorings and perfect matchings, take on a decidedly different flavor when topological constraints are placed on the structures involved. For example, the integer lattice $\mathbb{Z}^2$ is easy to tile with perfect squares of arbitrary size, but this is no longer generally possible in a continuous way when the group acts on a nice space.
We investigate a particular action of this group, the free part of the Bernoulli shift, and analyze two problems left open in the very recent paper of Gao-Jackson-Krohne-Seward. One concerns the existence of a clopen set which meets each connected component in two lines. The other seeks to characterize those graphs to which the Bernoulli shift continuously homomorphs. We attempted to prove that such line section exists, and to streamline the proof that there exists a continuous homomorphism from the Bernoulli shift to any odd wheel graph.
► Multicolor Ramsey Numbers for Small Hypergraphs
Emily Zhu
Advisor: Thomas Bohman
Abstract: In Ramsey Theory, a Ramsey number refers to the smallest size of a combinatorial object required to guarantee the existence of a certain substructure. For a multicolor Ramsey number, we consider coloring our object with an increasing number of colors and seek a copy of our substructure in some color. The most natural multicolor Ramsey number for graphs is that for the triangle, where current bounds are still fairly loose--the lower bound is exponential while the upper bound is factorial. We study related problems for hypergraphs, where a $k$-uniform hypergraph is a system of groups of points where every group has exactly $k$ points. Although asymptotically tight bounds are known for some multicolor Ramsey numbers of small 3-uniform hypergraphs, these bounds are not always exact.
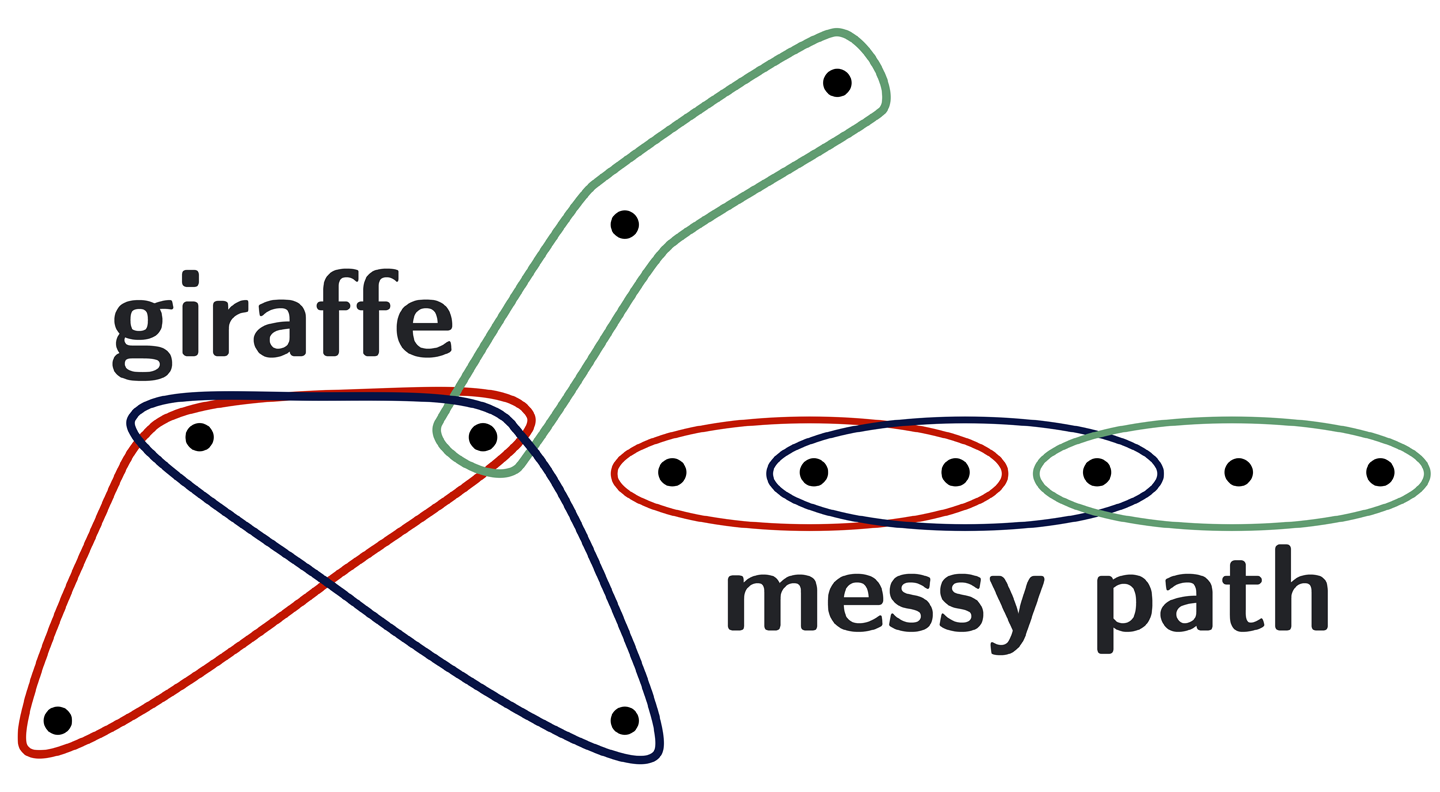
We consider this problem for a few more 3-uniform hypergraphs with 3 edges and provide new bounds for the multicolor Ramsey numbers for some of these hypergraphs, including the giraffe and messy path.
2018 Team

Students: David Altizio, Bryan Ding, Wenxin Ding, Shuyang (Serena) Gao, Varun Gudibanda, Yong Gun Choe, Zhiyang He, Ruoyuan Liu, Jung Joo Suh, Zilin Wang, Xinyu Wu, Yuepeng Yang, Taisuke Yasuda, Novdano Dede Yusuf, Emily Zhu
Faculty: Thomas Bohman, Clinton Conley, Elnur Emrah, Yu Gu, David Handron, Jason Howell, Dejan Slepčev, Michael Tait, Ian Tice, Tomasz Tkocz

