CMU Mathematics Undergraduate Research, 2020

Summertime traditionally ushers in a flurry of out-of-class activities for mathematics students at Carnegie Mellon University. Many of them disperse, traveling home, studying abroad, participating in research experiences at other universities, or taking internships in the finance or software engineering industries. But, in early 2020, as the global coronavirus pandemic brought the world to a screeching halt, many of our students found that their summer programs had been cancelled. Many of these students were very interested in using this suddenly free summer to engage with open ended-projects in mathematics. In response to this demand, the Department of Mathematical Sciences curated a brand new summer program: Summer Experiences in Mathematical Sciences (SEMS). This program was offered in parallel with the traditional SURF program, which provides stipends to students who stay at CMU in the summer months to work on research projects. SURF was itself much larger than normal this year, and both SURF and SEMS were conducted virtually in the summer of 2020. Find below details of the projects conducted in the summer of 2020 under the auspices of the SURF and SEMS program.
▼ SURF projects
► Neural Network Based Model Approximation for Discovering Dynamical Systems
Neil Chen, Daria Mashanova, Hannah Milano, and Mukund Subramaniam
Advisor: Hayden Schaeffer
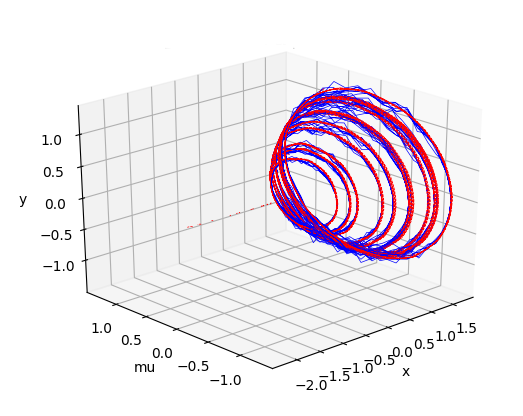
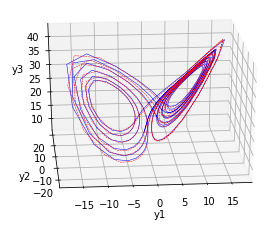
Abstract: In this research, we developed a neural network based approach to discover the underlying system of equations that govern some unknown dynamical systems. The idea is to approximate the forward flow of some unknown system only using the data. We parameterized the unknown velocity field by a shallow neural network with a moderate number of free parameters and fit it to the (noisy) data using a higher-order Runge-Kutta approximation. Additional prior information can be incorporated into the minimization. Using the learned velocity field, we can re-simulate dynamics (in order to clean the data) or predict the future states for new data (i.e. forecasting).
The figures highlight some of our results on the Hopf bifurcation and Lorenz systems.
The red curves are our simulation using the learned dynamical system while the blue curves are sample trajectories from the noisy training set.
► Numerical Scheme for Allen-Cahn Equation and Its Energy Stability
Zhijie Chen
Advisor: Franziska Weber
Abstract: The project implements an algorithm (in MATLAB) for approximating a solution for Allen-Cahn equations, a class of partial differential equations. This class of equations models the physical process of phase separation. Since we cannot hope to solve these partial differential equations analytically, we turn to numerical methods for a stable and accurate approximation.
We designed and implemented the scheme using Newton's method and showed that the scheme produced a solution that is stable with respect to some discrete energy, which is based upon the analytic energy of the actual Allen-Cahn equation. The bound on the energy of the solution gives us a bound on the discrete H1 norm of the approximated solution. As we proved that the bound on the discrete H1 norm is independent of the mesh size, we can then conclude that as the mesh size approaches 0, our scheme indeed converges in L2.
► Weakly cop win infinite graphs
Minsung Cho
Advisor: David Offner
Abstract: The game of Cops and Robber is a two-player perfect information game played on a graph, where a cop and robber alternate turns where they may move to adjacent vertices. The goal of the cop is to catch the robber, while the goal of the robber is to avoid capture, and if one cop can catch the robber on a graph, that graph is called a cop win graph. For finite graphs, it is known that a graph is cop win if and only if it is constructible, i.e. it can be built by successively adding vertices where the closed neighborhood of the added vertex is a subset of the closed neighborhood of a vertex already in the graph. We call an infinite graph weakly cop win if the cop can prevent the robber from returning to any given vertex infinitely often.
It is an open question whether weakly cop win graphs must be constructible. In our research, we make progress toward resolving this question by analyzing block graphs. Among other results, we prove necessary and sufficient conditions for an infinite graph with constructible blocks to be weakly cop-win.
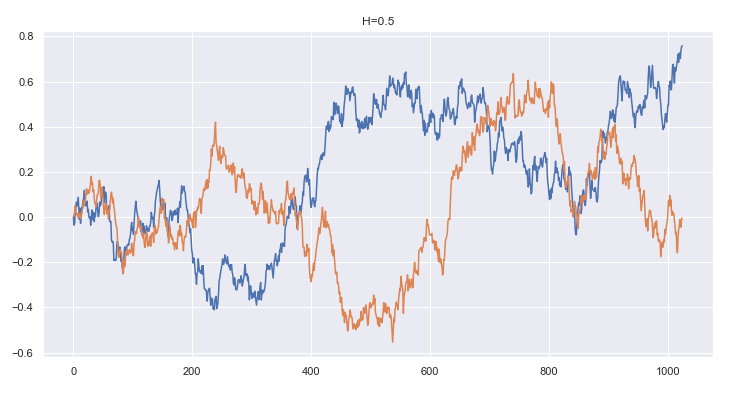
► Self-avoiding property of multi-dimensional Gaussian processes
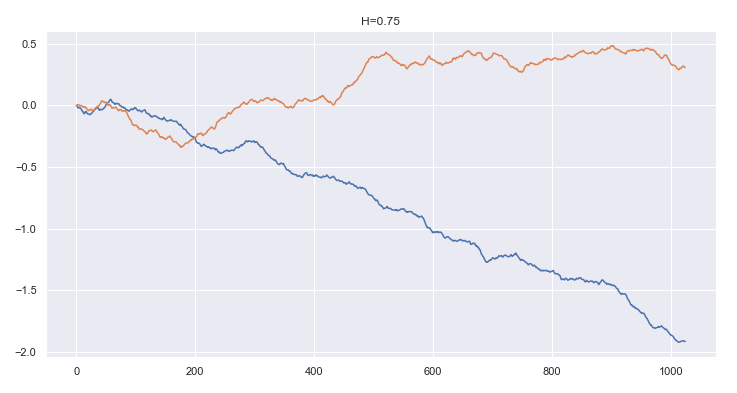
Yidan Hu
Advisor: Jiawei Li
Abstract: Gaussian processes are useful stochastic processes that can be used in statistical models. One important Gaussian process is fractional Brownian motion. Fractional Brownian motions (fBMs) are continuous Gaussian processes with a wide range of applications in various fields. In this project, we focused on the self-avoiding property of fBMs, which is the behavior that the random path of fBM intersect with itself. We modelled two fBM paths of dimension one with different Hurst parameters to observe this behaviour. Naturally we have that when the dimension of the process increases, the probability that its paths are self-intersecting decreases. Our goal is to find at what dimension, the self-intersecting behavior will disappear for fBM sample paths. To this end, we based on several geometric observation and establish several useful tail estimates, then utilized its Gaussian property to conclude the required result. This method can be generalized to all stationary centered Gaussian processes.
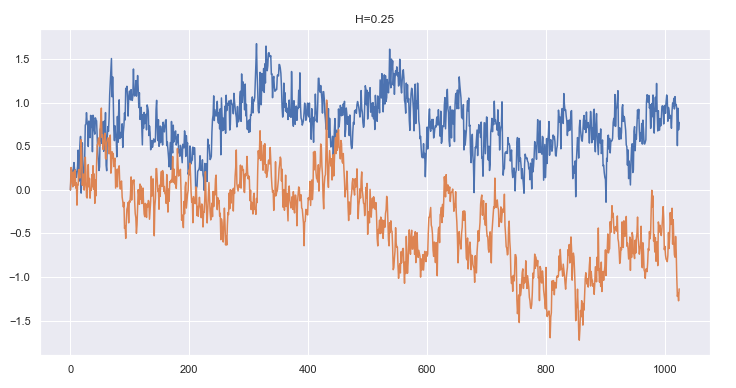
► Improving the Ramsey Bounds on Berge-K3 Hypergraphs
Chloe Ireland
Advisor: Thomas Bohman
Abstract: For a simple graph $G$, the Berge-$G$ family of hypergraphs is the set of hypergraphs $H$ with $|E(G)|$ hyperedges whose edges and vertices obey the rules of the following mapping. Let $f: V(G) -> V(H)$ be an injective map such that for every edge $xy$ in $E(G)$, there is a hyperedge $e_{xy}$ in $E(H)$ such that $f(x), f(y) \in e_{xy}$. Moreover, if $xy \neq x'y'$, then $e_{xy} \neq e_{x'y'}$. We create new tools--namely, a structural characterization of Berge $K_3$-free hypergraphs--to improve the bounds on the Ramsey number for Berge-$K_33$ hypergraphs that Maria Axenovich and András Gyárfás establish in their paper "A note on Ramsey numbers for Berge-$G$ hypergraphs."
► Surfactant Dynamics from the Arnold Perspective
Jonathan Jenkins, Carolyn Lee, Yuxuan Liu, Ethan Lu, and Desmond Reed
Advisor: Ian Tice
Abstract: In 1966, V. Arnold established an important connection between the incompressible Euler equations and a particular set of geodesic flows, using variational techniques to characterize the latter as solutions to the former. Motivated by his results, we similarly investigate a series of PDEs characterizing constrained minimizers of energy functionals, paying particular interest to those associated with surfactant dynamics.
Starting with the Arnold equation, we introduce terms associated to potential energies, surface tension and surfactant momentum to the potential to derive various PDEs.
► An Invisible Search Game
Eugene Lee
Advisor: Anton Bernshteyn
Abstract: We analyze a variant of the search-evasion game where the intruder occupies vertices, is "slow", in that they are allowed to move only to adjacent vertices or remain in place, and "invisible", in that the searchers operate with no knowledge of the position of the intruder, but are allowed to search arbitrary vertices on the graph. We introduce the notion of a topological search number, a quantity that captures the limiting behavior of the number of searchers necessary under subdivisions of a fixed graph.
Our central theorem provides a full algorithmically-verifiable classification of graphs with topological search number up to 3. Specific corollaries of our result show that prior bounds involving the pathwidth of a graph can fail to an arbitrary degree.
► Khinchin-type inequalities
Alexander Lum-Havrilla
Advisor: Tomasz Tkocz
Abstract: This project is devoted to sharp moment comparison inequalities for weighted sums of independent random variables (a.k.a. Khinchin inequalities).
We establish such inequalities for moments of all even orders for the so-called type L random variables, originating in statistical mechanics in Lee-Yang type theorems. Thanks to those theorems, we are also able to treat sums with ferromagnetic dependencies in a nonnegative external magnetic field. This extends Newman's results. We also compare the notions of type L, ultra sub-Gaussianity (introduced by Nayar and Oleszkiewicz) and strong log-concavity (introduced by Gurvits), and show that the latter two are in fact equivalent.
► Nonlinear Cantilever Limit Cycle Oscillations
Anrey Peng
Advisor: Jason Howell
Abstract: In this research, we examine limit cycle oscillations in a cantilever configuration. In this configuration, a thin beam is clamped on one end, and fixed on the other. Fluid flows from the clamped end toward the free end, inducing deflections in the beam. This motion is relevant to several modern applications, primarily the purposes of harvesting energy, in the form of piezoelectric devices. We consider a finite difference analysis and a modal analysis of the partial differential equations (PDEs) that govern this model to predict stability and frequency of limit cycle oscillations.
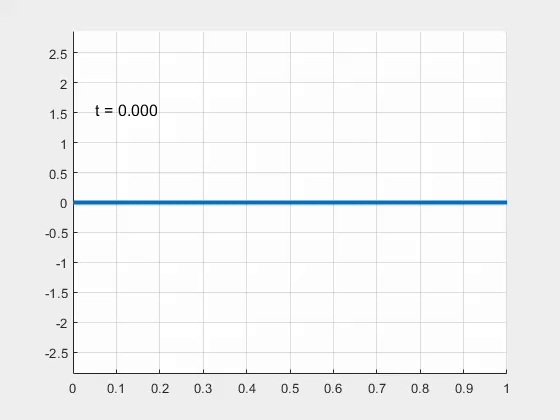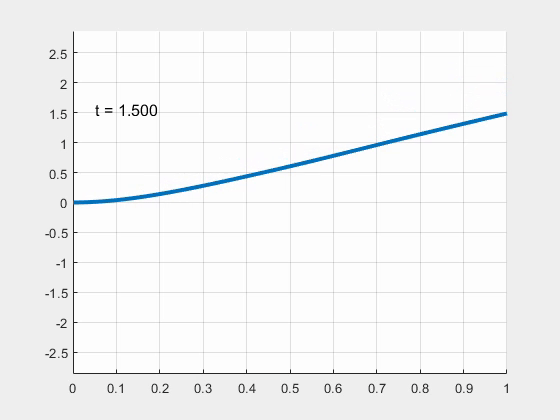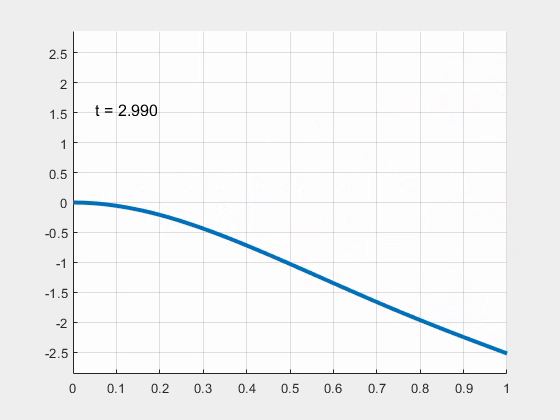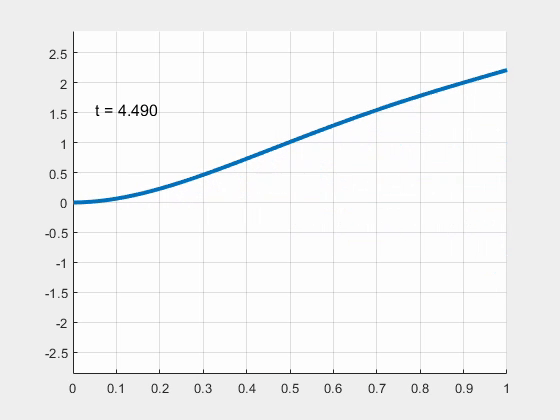
Furthermore, we examine various initial parameters of the beam to determine their effects on stability.
► Lonely Runners and Coprime Mappings
Fei Peng
Advisor: Thomas Bohman
Abstract: Imagine $n$ runners with distinct integer speeds running on a circular track with perimeter $1$, starting at the same position. A runner is lonely if nobody else is at distance less than $1/n$ away. The lonely runner conjecture states that each runner is lonely at some time. We show that this holds when the speeds differ by at most $(2-o(1))n$. This is an approximate version of a natural next step suggested by Tao. The key ingredient in our proof is a result on coprime mappings. Let $A$ and $B$ be sets of integers.

A bijection $f:A \to B$ is a coprime mapping if $a$ and $f(a)$ are always coprime. We show that if $A,B \subset [n]$ are intervals of size $2m$ where $m > e^{O((\log\log n)^2)}$ then there is a coprime mapping from $A$ to $B$.
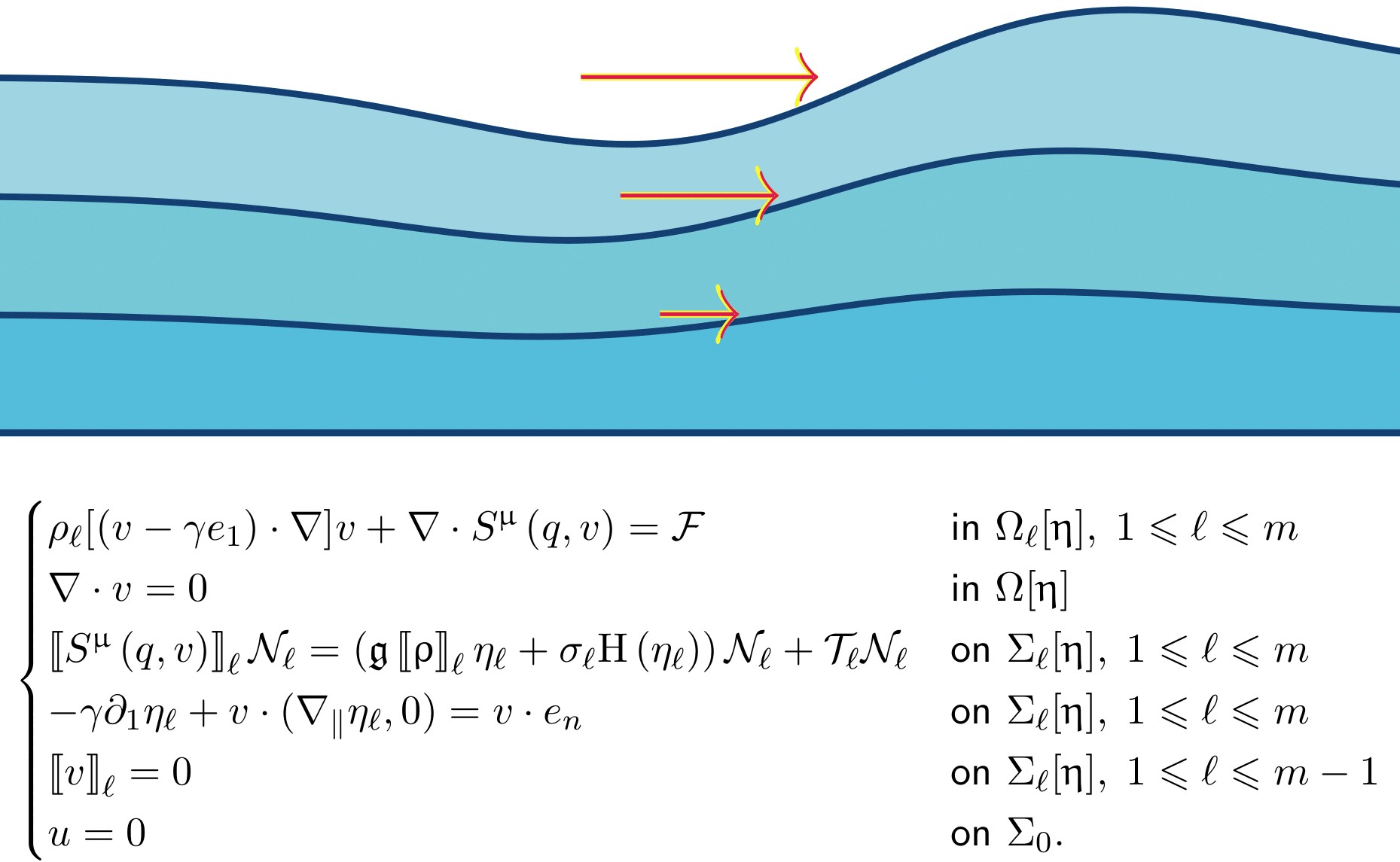
► Traveling Wave Solutions to the Multilayer Free Boundary Incompressible Navier-Stokes Equations
Noah Stevenson
Advisor: Ian Tice
Abstract: For a natural number m≥2, we study m layers of finite depth, horizontally infinite, viscous, and incompressible fluid bounded below by a flat rigid bottom. Adjacent layers meet at free interface regions, and the top layer is bounded above by a free boundary as well. A uniform gravitational field, normal to the rigid bottom, acts on the fluid. We assume that the fluid mass densities are strictly decreasing from bottom to top and consider the cases with and without surface tension acting on the free surfaces. In addition to these gravity-capillary effects, we allow a force to act on the bulk and external stress tensors to act on the free interface regions. Both of these additional forces are posited to be in traveling wave form: time-independent when viewed in a coordinate system moving at a constant, nontrivial velocity parallel to the lower rigid boundary.
Without surface tension in the case of two dimensional fluids and with all positive surface tensions in the higher dimensional cases, we prove that for small force and stress data there exists a traveling wave solution. The existence of traveling wave solutions to the one layer configuration (m=1) was recently established and this paper is the first construction of traveling wave solutions to the incompressible Navier-Stokes equations in the m-layer arrangement.
► Upper Bound of the Expectation of the Longest Common Sequence for a Large Alphabet
Zimu Xiang
Advisor: Boris Bukh
Abstract: Some previous studies have been made on the expectation of the longest common sequence of two randomly chosen words with the same length over some large alphabet of size $k$.
It has been determined that the constant $\gamma_k$, defined to be the limit of such expectation over the length, satisfies that $\gamma_k\sqrt{k}$ goes to 2 as $k$ grows. In this project, we first showed that the upper bound of the expectation exists if one of the two words is fixed, and used some similar method to find such an upper bound.
► Particle Filtering Method and its Application in Heat Diffusion Problem
Zhuqing Yang
Advisor: Yu Gu
Abstract: The majority stochastic processes based on the time are classical Ornstein-Uhlenbeck process with Gaussian property. However, non-Gaussian and high-frequency financial timeseries are more common in the real market, meaning that traditional statistical methods are insufficient to make predictions. To deeply explore the non-Gaussian situation, in this research, we applied the Particle Filtering (PF) method with Monte Carlo sampling in the stochastic process. PF has a substantial potential application in solving pricing with only partial data while managing large portfolios and pricing products by using the observed data to simulate the unobservable data. We observed that the accuracy of the model was enhanced based on using PF to predict the stochastic process's time series as the particle size increased, whereas the running efficiency decreased exponentially.
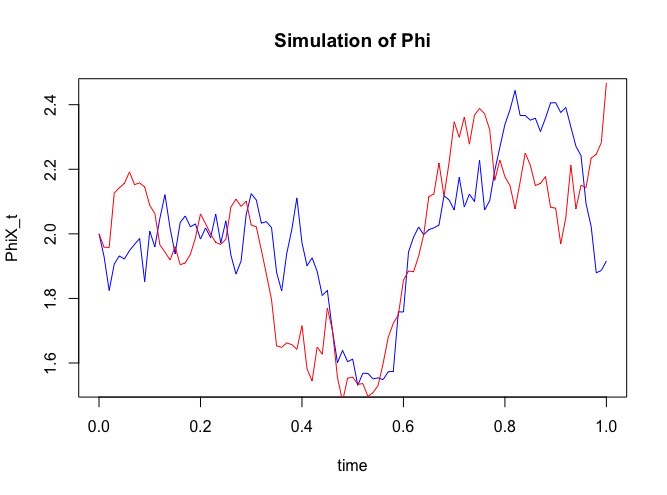
To approach the oversize dataset problem, we improved the original efficiency of O(N 2 ) to O(N) at best and O(NlogN) at worst by optimizing the resampling algorithm. In the line of the property of PF, we firmly believe it would have a wide range of applications, including pricing complex path-dependent European options, pricing American options, and numerically solving partially observed control and estimation problems.
► On log-rank conjecture for AND functions
Shanjiawen Zhao, Kevin Zhou, Vinod Krishnamoorthy
Advisor: Kaave Hosseini
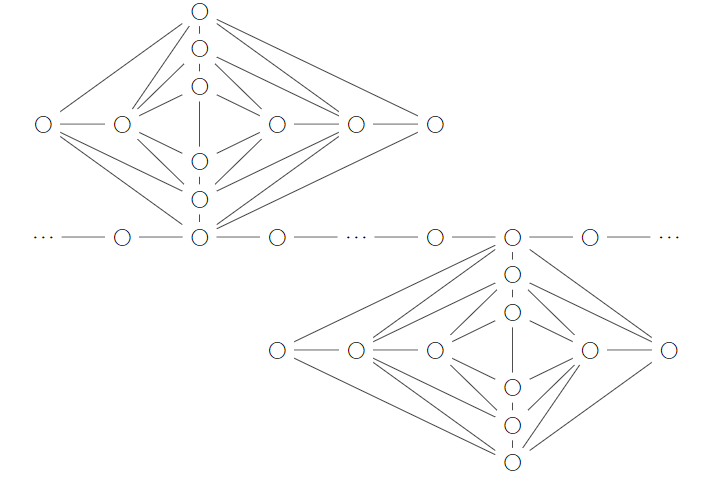
Abstract: log-rank conjecture, formulated in Lovasz and Saks in 1988 is one of the main problems in communication complexity and combinatorics. The conjecture basically shows that if a matrix with 0/1 entries has rank at most $r$, then the corresponding bipartite graph of the matrix could be partitioned to a quasipoly($r$) many bi-cliques and bi-independent sets. This conjecture is far from resolved. Here we study the log rank conjecture for a certain class of matrices called AND matrices. These are matrices formed by $M(x,y) = f(x$ AND $y) $ where $x, y$ are in ${0,1}^n$ and $f:{0,1}^n \to {0,1}$ is a Boolean function. This class of matrices contain many important families of matrices in the literature. We study the connection of this conjecture with combinatorics of hitting sets of set systems. We formulate a “fractional” and easier analog of the conjecture and show that to solve the actual conjecture, it’s enough to prove that fractional analog.
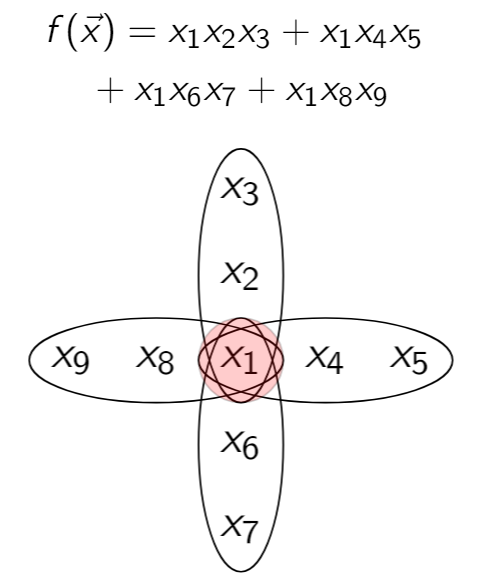
This figure highlights how a function written as polynomial corresponds to a sets system. Here the set system forms a sunflower, a structure that turns out to be crucial in the study of log-rank conjecture for AND functions.
► Entropy-regularized time-discrete optimal transport paths with multimarginal constraints
Alexander Zheng
Advisor: Robert Pego
Abstract: We study methods of characterizing and computing optimal probability distributions on time-discrete paths for an entropy-regularized kinetic energy functional, with specified marginal constraints at the discrete times.
Such problems generalize recent "light"-"speed" methods of numerically approximating the solution of optimal transport problems by Sinkhorn iterations. We minimize a Kullback-Leibler divergence for path probabilities relative to a Gibbs distribution for kinetic energies of linearly interpolated paths. We show optimizers take a simple reduced-data form amenable to approximation by cycling through Bregman projection steps. Then we verify that when one further optimizes over intermediate marginals, the minimizing distribution takes a form consistent with a diffusive optimal transport/control problem.
► Coarsening Regularity of Integer Partitions
Hongyi Zhou
Advisor: Boris Bukh
Abstract: Ramsey theory is a modern and arresting field of mathematics with a century of history.
The basic paradigm of Ramsey Theory is that any sufficiently large structure contains some highly ordered substructure. For instance, given any 6 persons, there are always 3 of them who are mutually friends or mutually strangers. In this research, we study the partitions and coarsenings of integers: we seek integers n such that, for any r-coloring of its t-partitions, there is a $k$-partition of $n$ all of whose $t$-coarsenings are of a same color.
▼ SEMS projects
► Neural Network Based Model Approximation for Discovering Dynamical Systems
Neil Chen, Daria Mashanova, Hannah Milano, and Mukund Subramaniam
Advisor: Hayden Schaeffer
Abstract: In this research, we developed a neural network based approach to discover the underlying system of equations that govern some unknown dynamical systems. The idea is to approximate the forward flow of some unknown system only using the data. We parameterized the unknown velocity field by a shallow neural network with a moderate number of free parameters and fit it to the (noisy) data using a higher-order Runge-Kutta approximation. Additional prior information can be incorporated into the minimization. Using the learned velocity field, we can re-simulate dynamics (in order to clean the data) or predict the future states for new data (i.e. forecasting).
The figures highlight some of our results on the Hopf bifurcation and Lorenz systems.
The red curves are our simulation using the learned dynamical system while the blue curves are sample trajectories from the noisy training set.


► Combinatorial Structures with Gaussian Weights
Yun Cheng, Albert Xu, and Yixue Liu
Advisor: Tomasz Tkocz
Abstract: We consider Gaussian versions of well-known results on average case analysis of classical optimization problems. Suppose that each edge of the complete graph on n vertices is assigned independently a weight which is a standard Gaussian random variable.
In this project, we determine asymptotic values as n tends to infinity of solutions to several classical optimization problems such as the minimum weight spanning tree, the assignment problem, the traveling salesperson. We also analyze the expected size of the minimum weight of a k-clique and more generally of a copy of a fixed balanced graph. For the upper bounds, we use tools from the theory of suprema of Gaussian processes. For the lower bounds, we rely on threshold results for random graphs.
► Detecting sumsets
Ari Fiorino, Eric Li, Justin Sun, Xiao Liu
Advisor: Kaave Hosseini
Abstract: Let A be a finite collection of integers. Can we write $A$ as $A=S+S$ where $S$ is some other set of integers, and $S+S=\{ s+s’: s,s’ \in S \}$? The answer depends on choice of A. Give input A, can we decide this quickly? Surprisingly the complexity of this basic problem is not understood at all. In this project we attack the problem in two directions.
First we obtain various partial results that suggest this problem is NP-Complete. We do this by obtaining a long sequence of polynomial time reductions between various problems. This chain of reductions falls short of proving this exact problem is hard, however we show a very similar looking problem about detecting multicolored cliques in graphs is NP-Complete. In the other direction we study the algorithmic approaches to obtain (approximate) solutions to this problem. We discover several heuristics based on integers programing and algebra of polynomials over finite fields to solve this problem.
► Sparse Approximation of High Dimensional Functions and Its Application to Learning Governing Equations
Vanessa Jiang and Ben Yuan
Advisor: Hayden Schaeffer
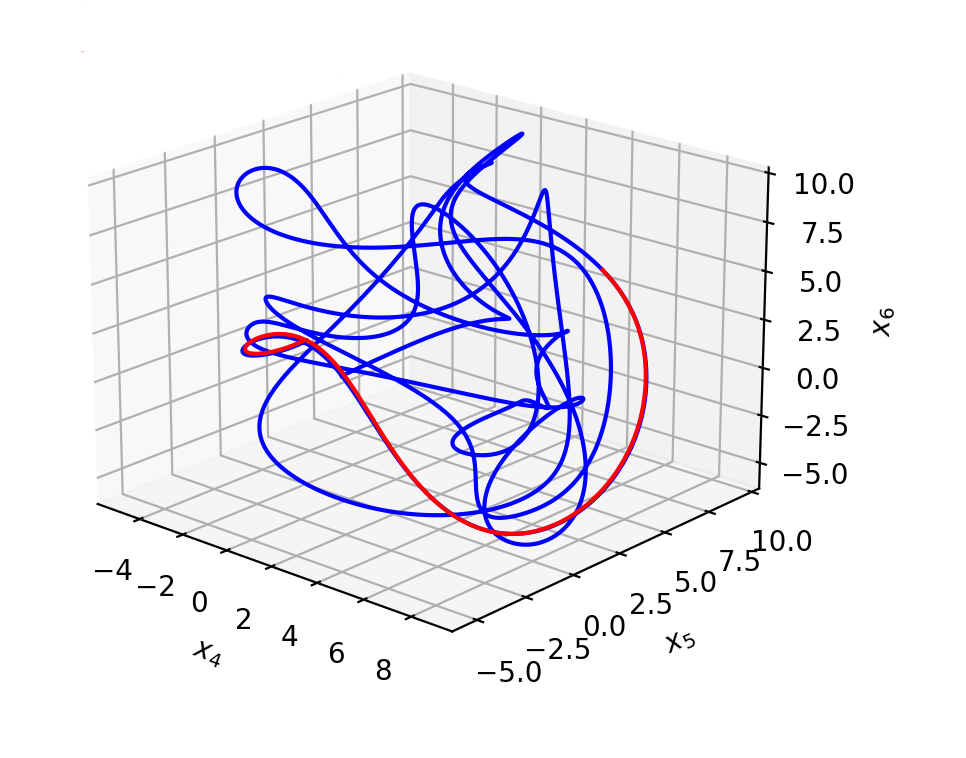
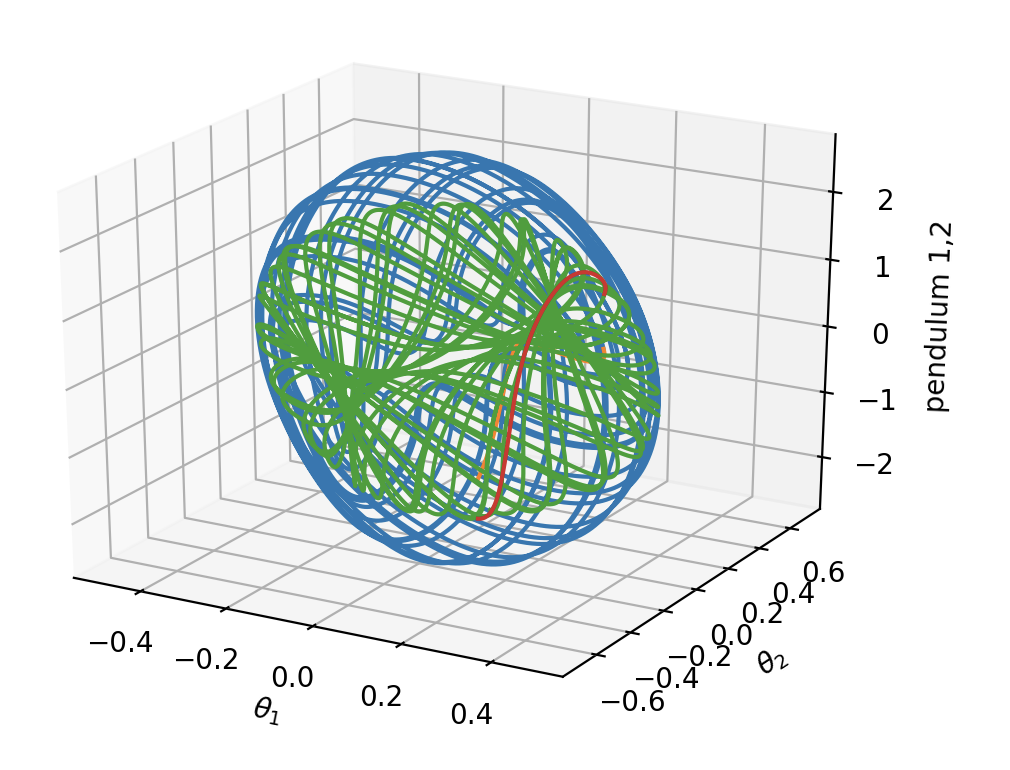
Abstract: This research focuses on sparse optimization based methods for approximating high-dimensional functions. The goal is to learn the generating equations given a small set of samples. Our modeling assumption is that the state variables come from some differential equation; however, the exact form of the equations are not given. We approximate the equations directly on the data by learning the coefficients with respect to either a set of orthogonal polynomials or a trigonometric basis. Since we have few samples relative to the number of unknowns, the linear problem is under-determined. By leveraging the sparsity-of-effect principle, we can assume that we only need a small number of candidate functions to represent the data. This assumption makes our problem computationally tractable via an L1 minimization problem. We use the L1 basis pursuit problem to determine the coefficients. We can show that the system is robust and stable, using results from approximation theory and compressive sensing.
Included are two examples from our summer work: the Lorenz 96 model and the double pendulum system. The blue (and green) curves are the true trajectories (not known to the user) and the red (and orange curves) are part of our predicted trajectories using our learned system.
► Structure of complement of sum-free sets
Tudor-Dimitrie Popescu, Xinjie He, Ling Hu
Advisor: Kaave Hosseini
Abstract: Let A be a subset of $F_2^n$ (the n dimensional vector space over the field with 2 elements.) Suppose A is sumfree, meaning if $x,y\in A$ then $x+y \notin A$. Sumfree sets have been widely studied in additive combinatorics.
Here we obtain some results suggesting that complement of sumfree sets must be highly structured. We employ some Fourier analytic techniques combined with additive combinatorics to show that the complement of any sumfree set contains a subspace of dimension at least $\Omega(n/log n)$. On the other hand we construct an example showing that this bound can not be improved to more than $2n/3$. We further study generalizations of the notion of sumfree set, as sets avoiding $d$-dimensional subspaces and similar conjectures in that setting.
► On log-rank conjecture for AND functions
Shanjiawen Zhao, Kevin Zhou, Vinod Krishnamoorthy
Advisor: Kaave Hosseini
Abstract: log-rank conjecture, formulated in Lovasz and Saks in 1988 is one of the main problems in communication complexity and combinatorics. The conjecture basically shows that if a matrix with 0/1 entries has rank at most $r$, then the corresponding bipartite graph of the matrix could be partitioned to a quasipoly($r$) many bi-cliques and bi-independent sets. This conjecture is far from resolved. Here we study the log rank conjecture for a certain class of matrices called AND matrices. These are matrices formed by $M(x,y) = f(x$ AND $y) $ where $x, y$ are in ${0,1}^n$ and $f:{0,1}^n \to {0,1}$ is a Boolean function. This class of matrices contain many important families of matrices in the literature. We study the connection of this conjecture with combinatorics of hitting sets of set systems. We formulate a “fractional” and easier analog of the conjecture and show that to solve the actual conjecture, it’s enough to prove that fractional analog.

This figure highlights how a function written as polynomial corresponds to a sets system. Here the set system forms a sunflower, a structure that turns out to be crucial in the study of log-rank conjecture for AND functions.
2020 SURF team
Students: Neil Chen, Zhijie Chen, Minsung Cho, Yidan Hu, Chloe Ireland, Jonathan Jenkins, Carolyn Lee, Eugene Lee, Yuxuan Liu, Ethan Lu, Alexander Lum-Havrilla, Daria Mashanova, Hannah Milano, Anrey Peng, Fei Peng, Desmond Reed, Noah Stevenson, Mukund Subramaniam, Zimu Xiang, Zhuqing Yang, Shanjiawen Zhao, Alexander Zheng, Hongyi Zhou
Faculty: Anton Bernshteyn, Thomas Bohman, Boris Bukh, Yu Gu, Kaave Hosseini, Jason Howell, Jiawei Li, David Offner, Robert Pego, Hayden Schaeffer, Ian Tice, Tomasz Tkocz, Franziska Weber
2020 SEMS research team
Students: Neil Chen, Yun Cheng, Ari Fiorino, Xinjie He, Ling Hu, Vanessa Jiang, Vinod Krishnamoorthy, Eric Li, Xiao Liu, Yixue Liu, Daria Mashanova, Hannah Milano, Tudor-Dimitrie Popescu, Mukund Subramaniam, Justin Sun, Albert Xu, Ben Yuan, Kevin Zhou
Faculty: Kaave Hosseini, Hayden Schaeffer, Tomasz Tkocz