Summer Undergraduate Applied Mathematics Institute
May 31 - July 26, 2016
Projects
► Exploring Origami Generated Structures in ${C}$, Yu Xuan Hong (download paper)
Advisor: Greggo Johnson
Abstract: The origami generator problem can be described as follows: given a set $U$ of angles, and a set $S$ of points containing 0 and 1, construct lines at angles in $U$ from each point in $S$ and from all possible intersection points of constructed lines, the set $R(U)$ is the closure of all possible points (including initial points) generated by such action. Previous research has shown many properties regarding the algebraic and geometric structures of $R(U)$, given $U$ and $S$ satisfying certain conditions. In particular, results have been proven for cases where $1 \in U$ and $S=\{0,1\}$.
In this paper, we venture beyond these restrictions to explore results for more general cases of $U$ and $S$. Our main results hold for cases where $U$ does not contain 1, and when $|S| \geq 2$. We will state and prove the conditions in those cases for $R(U)$ to be a lattice or a ring.

► Fractal Behavior of the Fibonomial Triangle Modulo Prime $p$, where the Rank of Apparition of $p$ is $p+1$, Michael DeBellevue, Ekaterina Kryuchkova (download paper)
Advisor: Greggo Johnson
Abstract: Pascal's triangle is known to exhibit fractal behavior modulo prime numbers. We tackle the analogous notion in the fibonomial triangle modulo prime $p$ with the rank of apparition $p^*=p+1$, proving that these objects form a structure similar to the Sierpinski Gasket. Within a large triangle of $p^* p^{m+1}$ many rows, in the $i^{th}$ triangle from the top and the $j^{th}$ triangle from the left, $\binom{n+ip^*p^m}{k+jp^*p^m}_F$ is divisible by $p$ if and only if $\binom{n}{k}_F$ is divisible by $p$. This proves the existence of the recurring triangles of zeroes which are the principal component of the Sierpinski Gasket.
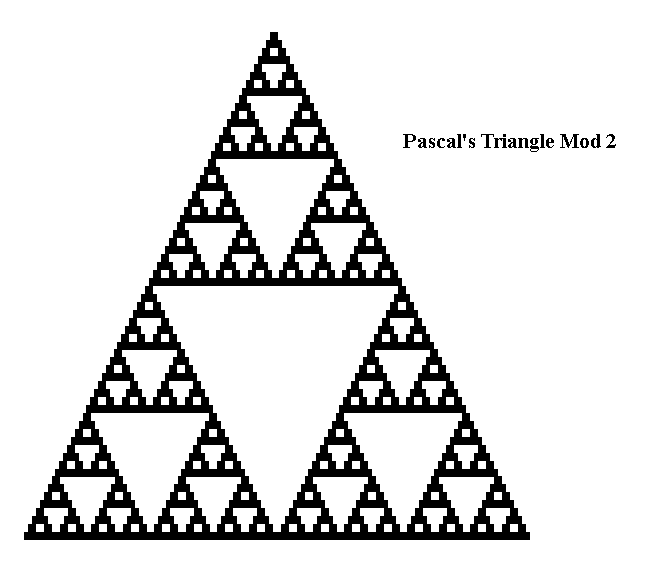
The exact congruence classes follow the relationship $\binom{n+ip^*p^m}{k+jp^*p^m}_F\equiv_p(-1)^{ik-nj}\binom{i}{j}\binom{n}{k}_F$, where $0\leq n,k$ < $p^*p^m$. It is a known result that the Fibonacci sequence modulo an integer is periodic. Denote the period modulo $p$ $\pi(p)$.
► Turán numbers of vertex-disjoint cliques in $r$-partite graphs, Adam Kapilow, Anna Schenfisch (download paper)
Advisor: Michael Young
Abstract: The Turán number of a pair of graphs $G$ and $H$ is denoted $ex(G,H)$, and is the maximum number of edges a subgraph of $G$ may have and still contain no copy of $H$.
In this paper, we determine $ex(K_{a_1,a_2,...,a_r}, mK_r)$, where $K_{a_1,a_2,...,a_r}$ denotes a complete $r$-partite graph with part sizes $a_1,...,a_r$ and $mK_r$ denotes $m$ vertex-disjoint copies of $K_r$, the complete graph on $r$ vertices. We prove that for any integers $1 \leq m \leq a_1 \leq a_2 \leq ... \leq a_r$ we have \[ex(K_{a_1,a_2, ... , a_r}, mK_r) = \sum \limits_{1\leq i < j \leq r}a_ia_j - a_1a_2 + a_2(m-1). \]
Discrete Mathematics: to appear
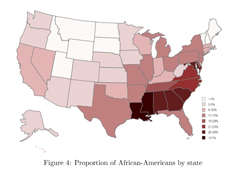
► Change in State: using Markov chains to explore national economic mobility and the evolving American Dream, Daniel Ayasse, Emily Myers, Christian Schmidt, Allison Schwam (download paper)
Advisor: Aris Winger
Abstract: By classifying the economic status of children and their parents into equal quintiles, it is possible to use Markov chains to provide general statements about intergenerational economic mobility. Using income tax records from over 40 million children and their parents, we examine the evolution of the probability of achieving the "American Dream" over three generations.
We then explore areas found to have greater upward mobility and attempt to identify contributing factors and trends. Our findings show a moderately high, negative correlation between attainability of the American Dream and race.
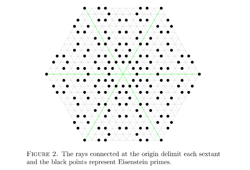
► $\tau$-Norm-Perfect and $\tau$-Perfect Eisenstein Integers for $\tau=\omega+2$ and $2$, Carlos Rojas Mena (download paper)
Advisor: Greggo Johnson
Abstract: Using Robert Spira's [4] definitions of complex Mersenne numbers and the complex sum-of-divisors function, we characterize $(\omega+2)$-norm-perfect and $(\omega+2)$-perfect numbers that are divisble by $\omega+2$ and prove the nonexistence of $2$-norm-perfect numbers that are divisible by $2$ in the Eisenstein integers.
Students
- Daniel Ayasse, Missouri State University
- Michael DeBellevue, University of Texas, Arlington
- Adam Kapilow, Swarthmore College
- Emily Myers, Smith College
- Carlos Rojas Mena, University of Rochester
- Christian Schmid, Carnegie Mellon University
- Anna Schenfisch, University of Wyoming
- Alison Schwam, University of Maryland, College Park
- Yu Xuan Hong, Pomona College
- Ekaterina Kryuchkova, Brown University
Group photo

Faculty

Dave Handron, Associate Teaching Professor
Course: Symbolic Programming in Mathematics
Project Director
E-mail: handron@andrew.cmu.edu
Wean Hall 6214
412-268-5583

Gregory Johnson, Assistant Teaching Professor
Project Director
E-mail: greggo@andrew.cmu.edu
Wean Hall 8122
412-268-1504

David E. Offner, Associate Professor, Westminster College
Course: Cryptography
E-mail: offnerde@westminster.edu

Michael Young, Assistant Professor, Iowa State University
Project Director
E-mail: myoung@iastate.edu
