2022 Summer Experiences in Mathematical Sciences
The Department of Mathematical Sciences is happy to offer an opportunity for research and study in mathematics in the summer of 2022. This program (SEMS) is offered free of charge to Carnegie Mellon students in good standing who are math majors. Students are expected to devote at least 20 hours a week to any research project they join. Students who have already made serious time commitments in the form of participating in internships, taking more than 10 units of summer courses or TAing in the summer should not apply for these experiences. Students who are receiving funding for summer research (through the SURF program or through faculty research grants) are not eligible to apply to participate in the research projects listed here.
Interested students must apply in order to participate. Acceptance into any particular SEMS project is not guaranteed. Furthermore, the department may cancel projects that do not generate sufficient demand. Students can join at most one of the research groups. Funding through faculty research awards may be available for some projects for students with excellent preparation for these projects.
Applications for SEMS 2022 are now closed.
Students who are accepted will be notified by the end of April.
Students who participate in SEMS are expected to attend the Undergraduate Summer Research Seminar in-person or on Zoom. The Undergraduate Summer Research Seminar will have one meeting each week from May 26 until June 26. The students are also expected to give a small presentation of their work at the SEMS symposium that will take place on Zoom in mid-August 2022.
Participating in SEMS qualifies students for SURA credit. For information on how to apply for SURA see https://www.cmu.edu/uro/summer research fellowships/sura/.
➤ Generalizations of the Erdős–Szekeres theorem
Advisor: Boris Bukh
Co-advisor: Zichao Dong
In 1935 Erdős and Szekeres proved that every sequence of $n$ distinct numbers contains a monotone (i.e. increasing or decreasing) subsequence of length at least $\sqrt{n}$. Furthermore, there are examples showing that $\sqrt{n}$ cannot be replaced by $1.01\sqrt{n}$, say. This project will investigate what happens when monotonicity is replaced by a more general property. For example, call a sequence $k$‑zigzag‑free if it contains fewer than $k$ local extrema. How long of a $k$‑zigzag‑free sequence can we always find inside a sequence of length $n$?
Prerequisites: Solid knowledge of the basics of combinatorics (e.g. 21-228 or 21-301).
May 16th - July 15th
Modality: In-person preferred.➤ Poking independent sets
Advisor: Boris Bukh
Co-advisor: Zichao Dong
A common idea in mathematics is to investigate resilience of a mathematical object to small changes. In this project, we examine large independent sets through this lens. Specifically, what happens if we declare certain vertices to be off-limits for independent sets? Can we necessarily make independent sets significantly smaller this way? Can we significantly reduce the number of independent sets in a graph this way? Though answers in certain settings are known, there are a number of open problems. This project will investigate these problems both in the context of graphs and in the context of other combinatorial structures, such as tournaments and hypergraphs.
Prerequisites: Solid knowledge of the basics of combinatorics (e.g. 21-228 or 21-301).
May 16th - July 15th
Modality: In-person preferred.➤ Realizing Convex Codes
Advisor: Amzi Jeffs
Given a collection of convex sets in $d$-dimensional space, one can write down a combinatorial code that describes how the sets intersect and cover one another. It is less easy to go in the opposite direction: given a code, can you find a collection of convex sets that realize it in space (i.e. a "drawing" of it)? What is the smallest dimension where you can do so? These questions are very hard in general but there are some interesting special cases where progress can be made - for example, what if we use boxes, or uniform balls, instead of convex sets? The goal of this project will be for students to learn and understand what convex codes are, some of the obstacles to realizing them, and to investigate new ways to realize certain classes of codes.
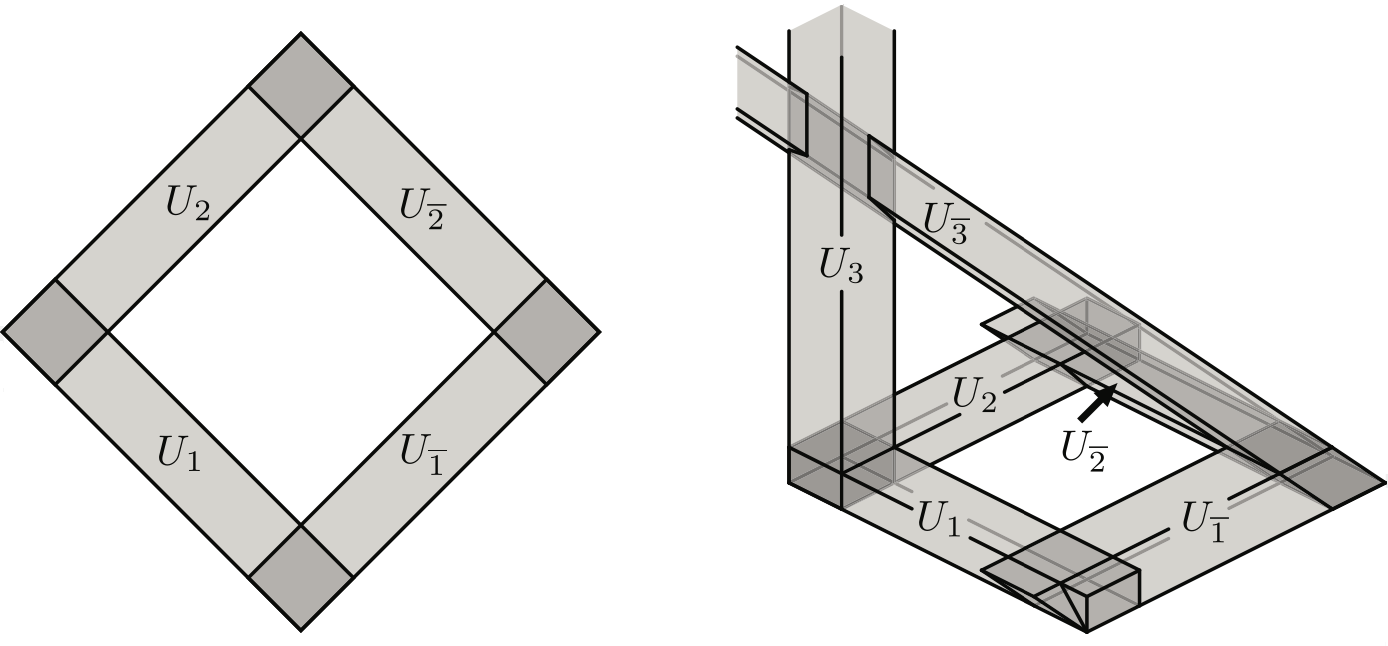
Prerequisites: Students should have experience with basic combinatorics. Some familiarity with geometry or topology will be useful, but not required.
June 6 - August 5
Modality: In-person.➤ Fiber products of planar graphs and the Sierpinski carpet
Advisor: Aristotelis Panagiotopoulos
Let $\mathcal{C}$ be the collection of all finite connected graphs. Then $\mathcal{C}$ is closed under several important operations. For example: the tensor product of any two graphs from $\mathcal{C}$ is in $\mathcal{C}$; the fiber product of any two surjective graph homomorphisms $f : B \to A$ and $f : C \to A$ with connected fibers is in $\mathcal{C},$ if so are $A, B$ and $C$. Based on these closure properties and a classical construction from logic (known as the Fraïssé construction) one can provide a canonical description of the "Menger sponge" - a fractal with very interesting dynamical properties. The goal of this project is to establish that the collection $\mathcal{P}$ of all finite connected ${\bf planar}$ graphs satisfies similar closure properties. These properties can be used together with the Fraïssé construction to provide a canonical description of another famous fractal known as the "Sierpinski carpet".

Prerequisites: This project is intended for students with strong background in combinatorics who are also interested in topology and/or logic. Combinatorics (21-301), or A in Discrete Mathematics (21-228), is a prerequisite. Priority will be given to students who took courses such as Graph Theory (21-484), Topology 21-465, Intermediate Logic 21-400, Set Theory (21-329).
May 20 - July 20 (can be adjusted)
Modality: Hybrid (on Zoom and in-person).➤ Random hypergraphs and stochastic topology
Advisor: Andrew Newman
Most questions about random graphs have to do with finding thresholds for certain properties, i.e. critical probabilities at which the likelihood of a graph having a particular property (e.g. being connected, containing a triangle, or being able to be drawn without crossing edges) jumps from zero to one. Over the last 20 years or so there has been interest in generalizing what we know about random graphs to random simplicial complexes (or equivalently random hypergraphs) especially from the point of view of topological properties (e.g. being simply connected, containing a high dimensional sphere, or being able to be drawn in some high-dimensional space). We will cover the basics of topology from a mostly combinatorial perspective as well as the standard random models and then, based on student interest, focus on one or two potential projects. No background in topology is required, although a course in probability (e.g. 21-325) is a prerequisite. Some potential projects may have a programming component, so some programming experience will be helpful, but not required.
Prerequisites: A probability course (21-325 or equivalent).
May 23 - July 15
Modality: In-person.➤ Nonstandard notions of discrepancy
Advisor: Peleg Michaeli
Co-advisor: Michael Sarantis
Suppose an adversary orients the edges of a Hamiltonian graph. We look for a Hamilton cycle with as many edges as possible pointing in the same direction. This problem has been studied for dense graphs (graphs with a large minimum degree) and random graphs. It is one example of a "nonstandard" notion of combinatorial discrepancy (the theory of "inevitable deviations from the mean") in the setting of graphs. In this project, we will survey several such notions, including multicolour, oriented and continuous discrepancies, in large generality. The goal would be to see if (and how) one can extend known results on (traditional) discrepancy to those variants.
Prerequisites: Combinatorics (21-301), or Graph Theory (21-484), or equivalent.
May 16 - July 8
Modality: In-person.➤ Rearrangements of functions
Advisor: Giovanni Leoni
This project deals with the theory of rearrangements of functions. The idea is to replace a function f defined on some subset of the real line (or, more generally, on some measure space) with another function $g$, defined on a possibly different set, which is more "symmetric" than $f$, but it has the same "size" of $f$. The size is measured in terms of the distribution function of $f$. It can be proved that the rearrangement of a function preserves many important quantities, such as the $L^{p}$ norm. There are several types of rearrangements: polarization, decreasing rearrangement, symmetric decreasing rearrangement, and so on. The goal of this project is to prove that if a function $f$ belongs to a "nice" class of functions, then its rearrangements stay in the same class.
Prerequisites: Students should be comfortable with standard concepts in analysis, mainly for functions of one variable. Students who have taken 21-269 Vector Analysis or 21-235 Principles of Real Analysis or Math Studies: Analysis I will have the necessary background.
Dates flexible except no meetings during the period June 17 - June 27.
Modality: In-person preferred.