➤ Dispersion in dimensions 2 and 3

Advisor: Boris Bukh

Suppose $n$ points are placed in a unit cube $[0,1]^d$. What is the largest axis-parallel box one can find that contains none of these points? This problem has been mostly studied for large $d$. The goal of the project is to learn about this problem, and to see if one can obtain good bounds in small dimensions both for this problem and for the analogous problem on the torus.

Prerequisites: Combinatorics (e.g. 21-301) and Analysis (e.g. 21-355 or 21-356).

June 14 - August 15

➤ Geometric Combinatorics

Advisor: Florian Frick

We will think about combinatorial problems geometrically and about geometric problems combinatorially. Associating geometric objects (such as polytopes, point sets, or topological spaces) to combinatorial ones will allow us to use a wide variety of methods for problems such as graph and hypergraph colorings, Ramsey-type results, and network flows. Conversely, we will try to understand geometry from the viewpoint of discrete mathematics and use combinatorial techniques to prove new results about the geometry of point sets in Euclidean space and related problems. The goal will be to learn interesting mathematics and produce new results.

Prerequisites: No geometric prerequisites are needed, but participants should expect to learn a substantial amount over the summer. Solid knowledge of the basics of combinatorics is required.

June 28 - August 20

➤ Subword Complexity of Binary Words

Advisor: Irina Gheorghiciuc

Let $A=\{ 0,1 \}$ be a binary alphabet. A subword of a word $w$ over $A$ is a block of consecutive letters of $w$. The subword complexity function of $w$ assigns to each positive integer $n$ the number $p_w(n)$ of distinct subwords of length $n$ of $w$. The subword complexity is also called symbolic or blockwise complexity. The general problem of determining which function can be the subword complexity function of an infinite (or even finite) word is very interesting and very hard. There are several known necessary conditions as well as several sufficient conditions for a function $f: \mathbb{N} \to \mathbb{N}$ to be a subword complexity function. In this project we will work on two problems: counting the number of distinct subword complexity functions of binary words of length $n$ (hard) and the relation between subword complexity and pattern avoidance in binary words (easier).

Prerequisites: A in 21-127 or 21-128, or A in 21-228 (preferred).

May 19 - July 14

➤ Decompositions of product graphs into fixed subgraphs

Advisor: David Offner

The $n$-dimensional hypercube graph $Q_n$ has vertex set $\{0,1\}^n$ and an edge between every pair of vertices that differs in exactly one coordinate. We consider edge decompositions of $Q_n$ into isomorphic copies of a given graph $H$. While a number of results are known about decomposing $Q_n$ into graphs from various classes, even the simplest cases of paths and cycles of a given length are not fully understood. For example, a conjecture of Erde asserts that if $n$ is even, $\ell < 2^n$ and $\ell$ divides the number of edges of $Q_n$, then $Q_n$ can be decomposed into paths of length $\ell$. Recent progress toward resolving Erde's conjecture proved that $Q_n$ can be decomposed into cycles of certain lengths up to $2^{n+1}/n$. As a consequence, $Q_n$ can be decomposed into copies of any path of length at most $2^{n}/n$ dividing the number of edges of $Q_n$, thereby settling Erde's conjecture up to a linear factor.

This project will seek to find necessary and sufficient conditions for decomposing the edge set of hypercube graphs into copies of a fixed subgraph, beginning with the open cases of paths and cycles. As the hypercube is an example of a graph produced by Cartesian products of cycles, we may also consider more general decomposition problems on this family of product graphs.

Prerequisites: 21-228 or 15-251.

June 7 - July 30

➤ Online algorithms

Advisor: David Offner

This project concerns online algorithms, which can be loosely translated as "mathematically making decisions that you won't later regret." More formally, an online algorithm does not receive all the input data in advance, but rather must make permanent decision while input data is given over time. Since the algorithm has incomplete information, it cannot make perfect decisions, but the goal is to make decisions that will closely approximate the retrospectively optimal decisions.

In the prophet problem, we are given $n$ probability distributions $D_1, ..., D_n$ up front, and then see independent draws $x_1 ~ D_1, ... , x_n ~ D_n$ one at a time. We must select or reject $x_i$ before seeing $x_{i+1}$ (we can only choose one $x_i$) and aim to maximize the expected value of our choice. We will investigate variants of the prophet problem and/or other discrete and probabilistic questions in online algorithms.

Prerequisites: 21-228 or 15-251.

June 7 - July 30

➤ Models for Coarsening in Inhomogeneous Solutions

Advisor: Raghavendra Venkatraman

Oswald Ripening is a phenomenon observed in solutions that describes the change of the shapes and sizes of crystals or sol particles over time:sol particles dissolve, and redeposit onto larger crystals or particles. As such, this is an instance of coarsening phenomena that describe patterns that evolve in time, with shapes staying somewhat recurrent, and length scales of shapes increasing in time (see Figures 1 below). Understanding of coarsening is also important from the viewpoint of grain growth in polycrystals. In this project we will study several simplified models for the growth of grains using tools from real analysis, ODEs and the calculus of variations. As an example of questions we might investigate, for instance, consider the evolution of droplets, such as those in Fig. 1 (b) below. It is natural to track the centers and radii of the droplets assuming they stay spheres.

• What can we say about the long time positions of the centers?
• Do the radii all become equal if we track this evolution for a long time?
• What if the number of these droplets becomes huge (mathematically, tends to infinity)? Do the droplets arrange themselves in a particular manner? A very difficult, but intriguing open question is to show that, in 2 dimensions, the droplets become equi-sized and their centers are arranged in a hexagonal lattice. We will work on accessible, (significantly) simplified, yet fascinating models.

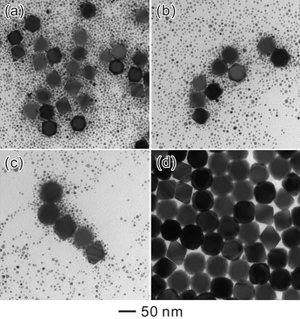Figure 1 (a) Oswald Ripening of Palladium nanoparticles in formaldehyde

Figure 1 (b) Droplets in thin liquid films

Prerequisites: Real analysis.

June 1 - July 31

➤ Modeling objective structures via Mean Periodic Functions

Advisor: Raghavendra Venkatraman

A function $f: \mathbb{R} \to \mathbb{C}$ is said to be mean periodic if there is a measure $\mu$ on $\mathbb{R}$ such that \begin{align*} \int_\mathbb{R} f(x-y) \,d \mu(y) = 0, \quad \quad x \in \mathbb{R}. \end{align*} This definition might seem intimidating at first, but it is a far-reaching generalization of periodic functions: take $\mu = \delta_a - \delta_0, a > 0$ and we recover $a-$ periodic functions, since the above equation requires $f(x - a) = f(x)$ for every $x \in \mathbb{R}.$ Mean periodic functions have rich approximation properties via polynomials, and elegant representation formulas using Fourier analysis. As such, akin to periodic functions, mean periodic functions encode valuable averaging properties. This project investigates the utility of mean periodic functions to study objective structures, a class of high functional materials. Before we say what these are, let us emphasize this: prerequisites for this project are still just analysis, and an interest in physics. I'll teach you whatever Fourier analysis/calculus of variations/ discrete differential geometry background you need, as we go along!

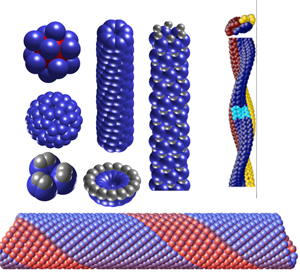
"Objective structures" are atomic structures made up of identical atoms that have the following property: up to reorienting yourself in the right way, you see the same environment sitting on any atom. Graphene, single-walled carbon nanotubes, buckyballs, many viral structures, all have this property. In this project we'll investigate modeling objective structures via mean periodic functions, and the extent to which we can leverage the averaging properties of such functions to inquire: what do objective structures look like, from far away?

Prerequisites: Real analysis.

June 1 - July 31

➤ MarketWatch Seminar

Advisor: William Hrusa

The idea behind MarketWatch Seminar is to provide guidance and experience in following Financial Markets and also in Giving Presentations. This seminar is aimed primarily at students who are considering careers in the Finance Industry.

There will be an initial meeting or two devoted to talking about Financial Markets and how to follow them. We will divide assets into 4 basic classes: (i) Equities; (ii) Interest Rate Products; (iii) Commodities; (iv) Currencies. Students will be formed into teams of 2 to 4 students per team (depending on how many students participate). Each team will be assigned one of the four asset classes each week and be expected to give a presentation on that asset class in front of the other teams. Weekly sessions will take approximately 90 minutes to 2 hours. If there is sufficient interest we can have different sections, e.g. a Tuesday Group of 4 teams and a Thursday Group of 4 teams.

June 1 - July 29