2025 Summer Experiences in Mathematical Sciences
The Department of Mathematical Sciences is happy to offer an opportunity for research and study in mathematics in the summer of 2025. This program (SEMS) is offered free of charge to Carnegie Mellon undergraduate students who satisfy the following eligibility requirements:
- Students have to be Carnegie Mellon undergraduate students majoring in mathematics.
- Students have to be in good standing.
- Students who participated in SEMS in previous years are not eligible to apply again.
- Students who have already made serious time commitments in the form of participating in internships, taking more than 12 units of summer courses or working as teaching assistants in the summer should not apply for this program.
- Students who participate in SEMS 2025 are expected to return to campus in the fall and give a small presentation of their work at the SEMS symposium that will take place in October.
- Students who are receiving funding for summer research (through the SURF program or through faculty research grants) are not eligible to apply for SEMS.
Interested students must apply in order to participate. Acceptance into any particular SEMS project is not guaranteed. Furthermore, the department may cancel projects that do not generate sufficient demand. Students can join at most one research group. Once accepted, students are expected to devote at least 20 hours a week to any research project they join. Note that SEMS does not provide funding for students.
Participating in SEMS qualifies students for SURA credit. Note that the SURA credit is not automatic. To receive this credit, students will need to enroll in SURA. See this page for instructions on how to enroll in SURA.
Applications for SEMS 2025 are now closed.
Students who are accepted will be notified by mid-April. Students who participate in SEMS are expected to attend the Undergraduate Summer Research Seminar in-person or on Zoom. The Undergraduate Summer Research Seminar will have one meeting each week from June 5 until July 3.
➤ Measurable Combinatorics on Planar Lattices
Advisor: Riley Thornton
You probably know the famous 4-color theorem: on any map you can color in the countries with 4 colors so that neighboring countries get different colors. This assumes the map is planar and every country is connected. But what if every country has to pick it's own color and they can only talk to their neighbors while they decide? Can they still coordinate to use 4 colors? And how long does it take? Or, what if the map is really really big and only looks planar up close? In this project we'll study these kinds of "local'' versions of problems for planar lattices as they appear in measurable combinatorics.

Prerequisites: Discrete Mathematics 21-228, or Combinatorics 21-301, or Probability 21-325, or Intermediate Real Analysis, or Descriptive Set Theory.
July 7 - August 22
Modality: In-person.➤ New Interpretations of $q$-Ballot Numbers
Advisor: Irina Gheorghiciuc
A lattice path is a path in $\mathbb{Z}^2$ which starts in some point $(x,y) \in \mathbb{Z}^2$ and consists of unit steps $(0,1)$ up and $(1,0)$ right. The ballot number $B(a,b)=\binom{a+b}{b}-\binom{a+b}{b+1}=\frac{b-a+1}{b+1}\binom{a+b}{b}$ counts the number of lattice paths from $(0, 0)$ to $(a, b)$ that never fall below the diagonal $y = x$. The ballot number $B(a,a)$ is called a Catalan number. In this project we will interpret several polynomial generalizations of ballot numbers in terms of lattice path statistics such as inversions $inv(w)$, descents $des(w)$, and the major statistics $maj(w)$, and explore the connections between different interpretations.
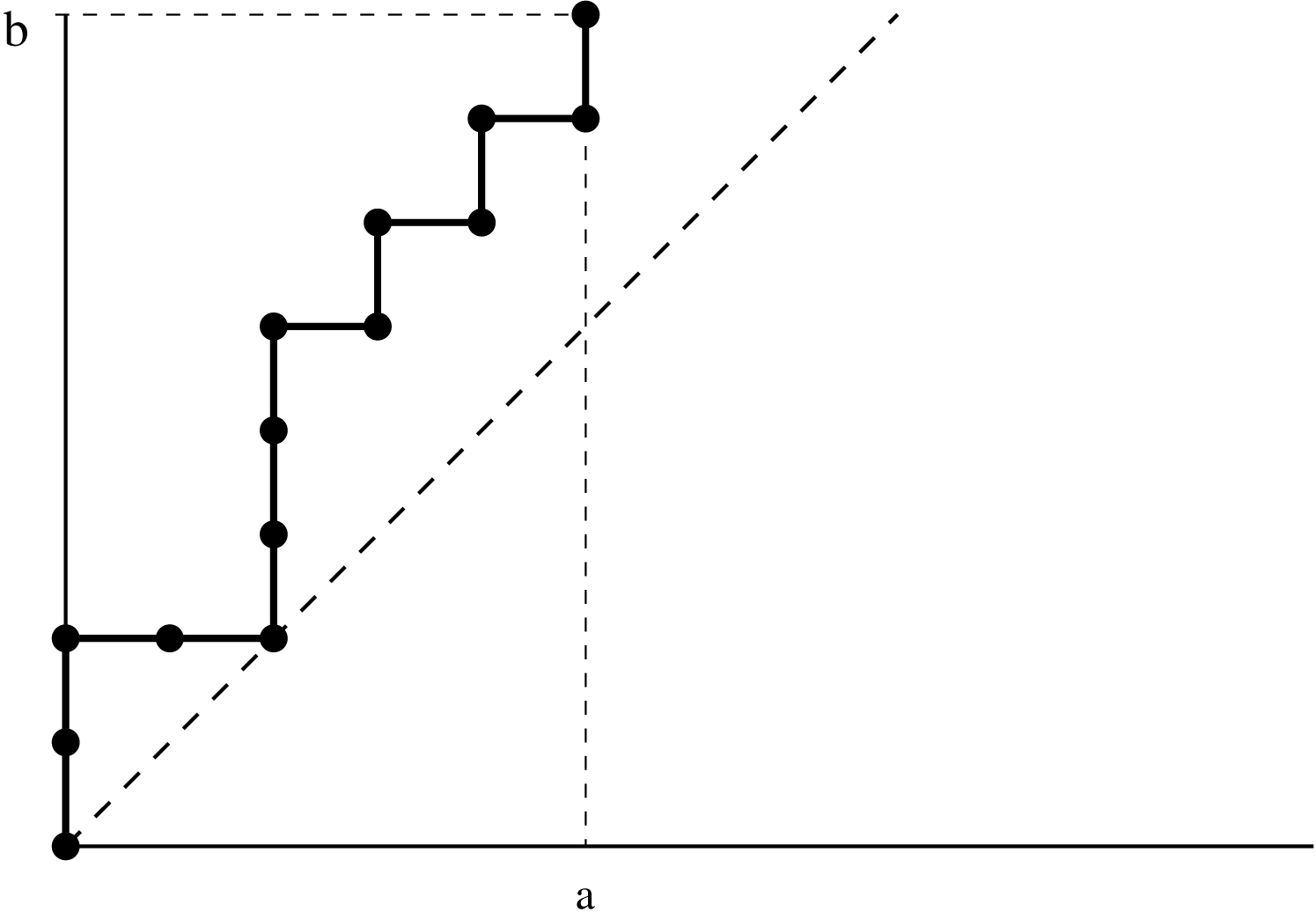
Prerequisites: Mathematical Concepts and Proofs (21-128) or equivalent with a grade of A, 21-228 or 21-301 or equivalent with a grade of at least B. Programming skills are highly appreciated.
May 12 - June 27
Modality: In-person.➤ Smoothing effects of Asplund summation
Advisors: Martin Rapaport and Tomasz Tkocz
The interplay between information theory and convex geometry has been very fruitful, resulting with many intriguing inequalities for entropy as well as for volume. This project aims at exploring such synergies in the context of the celebrated monotonicity of the entropy power. Specifically, suppose that $A$ is a bounded (measurable) subset in the plane. It is an open problem whether the area of the Minkowski (algebraic) sum $\frac{A+A}{2}$ has no larger area than the area of $\frac{A+A+A}{3}$. There is a tantalizing generalization of this problem for functions in terms of the integrals of a certain type of summation (Asplund convolution). We will learn fundamental results in the surrounding areas with the goal of attacking this or related open problems. This project would be ideal for anyone with interests in analysis, probability, combinatorics, and interactions of thereof.
 Figure 1. An example of sets $A$, $\frac{A+A}{2}$, $\frac{A+A+A}{3}$.
Figure 1. An example of sets $A$, $\frac{A+A}{2}$, $\frac{A+A+A}{3}$.Prerequisites: Analysis course (21-355 and 356 or equivalent), Linear algebra course (21-341 or equivalent), Probability course (21-325 or equivalent).
May 12 - June 27
Modality: In-person.➤ Free Boundary Problems
Advisor: Giovanni Leoni
A free boundary problem is mathematical problem where the solution is not only unknown but also part of the region in which it is defined is unknown and must be determined as part of the solution. One of the simplest examples of a free boundary problem is the obstacle problem. Imagine you have a thin, flexible membrane (like a stretched rubber sheet) lying over a fixed obstacle (like a bump). The membrane is pushed down by an external force (like gravity), but it cannot go below the obstacle. Mathematically, we describe this problem using differential inequalities. In this project, we will study free boundary problems involving functions of one variable.
Prerequisites: Students should be comfortable with standard concepts in analysis, mainly for functions of one variable. Students who have taken 21-269 Vector Analysis with a grade of B or higher or 21-235 Principles of Real Analysis or Math Studies: Analysis I with a grade of B or higher will have the necessary background.
June 23 - August 8
Modality: In-person.