Summer Undergraduate Applied Mathematics Institute
May 27 - July 22, 2014
Projects
► Matrix representations of finite configurations in the Hausdorff metric space, Kelly Kuzemchak, Sinem Semsioglu (download paper)
Advisor: Timothy Flaherty
Abstract: The Hausdorff metric provides us with a way to measure the distance between sets. We investigate properties of finite configurations in the Hausdorff metric space. Of particular interest are configuration numbers, that is, the number of finite sets at a specific location between two given finite sets.
We expand on the work of Steven Schlicker, et al., through which it has been found that 19 and 37 are not configuration numbers for any possible finite configuration. We further analyze configurations by representing them as binary matrices. In this way we can systematically compute possible configuration numbers. Additionally, we investigate the minimum dimension in which certain configurations can be represented.
► Characterization of unconfinable hexagonal cells, Larry Allen, Katherine Borst, Brittany Claiborne, Katherine Pilewski (download paper)
Advisor: Alexei Kolesnikov

Abstract: We address an open question posed by Alfeld, Piper, and Schumaker in 1987 and again by Alfeld in 2000 regarding the characterization of unconfinable cells. For cells with 6 interior edges, we obtain a geometric characterization of confinability in terms of cross-ratios. This characterization allows us to show that a hexagonal cell in which the diagonals intersect at the interior vertex is unconfinable if and only if the lines containing opposite edges and the diagonal through the remaining points are either parallel or are concurrent.
Computer Aided Geometric Design: Volume 45, July 2016, Pages 73-82
► Regression analysis: predicting depth of earthquakes, Woosub Shin (download paper)
Advisor: Chad Schafer
Abstract: The importance of predicting Earthquakes is increasing due to recent catastrophes such as those in Haiti and Japan. In this project we tried to predict the depth of hypocenters of earthquakes based on ISE-GEM catalog. Using Regression Tree we divided the Earth's surface into thirteen smaller regions, and classified them into five groups. On each group we applied General Additive Model(GAM) and Random Forests. In order to improve the result of the analysis we need to improve measuring methods as well as to filter to find more accurate data.
► Predicting call option prices using regression models, Munira Shahir (download paper)
Advisor: Chad Schafer
Abstract: One method to consists of predict call option prices is the Black-Scholes equation. However, that is utilizing for predicting European call option prices not American call option prices. The work done consisted of utilitizing regression models to predict call option prices utilizing known information from the New York Stock Exchange (NYSE).
► Calibrating a trinomial maple model to compute the current values of call options, Rebecca Spencer-Strong, Alexandra Van Neste (download paper)
Advisor: David Handron
Abstract: For this project, we looked into a trinomial model that would compute time-zero call prices based on real life data. Our approach involved using a Maple program. This program was a set of procedures that allowed us to input lists of historical stock prices and current strike prices from Yahoo Finance, a maturity date, an interest rate, and the current stock price. The output of the program was a list of call option prices corresponding to the inputted strike prices. The program began by computing a variance for the list of stock prices based on the expiration date.
Once it had this value for the variance of the growth rate, the program computed future stock price values to build a trinomial tree and then performed backwards induction on that tree. The backwards induction process calculated the call prices at time N in the tree and used those values to determine the time-zero call price of each call option. Our trinomial model gave us some flexibility because our risk-neutral probabilities had a free parameter. Having this free parameter allowed us to use the optimal risk-neutral values that resulted in the calculated call prices closest to the quoted call price values. The goal was to be able to calibrate our model so that it would fit market data well and potentially be useful in finding mispriced options. Maple allowed us to make the computations fast and relatively easy to adjust.
► Newton's Method on a system of nonlinear equations, Nicolle Eagan, George Hauser (download paper)
Advisor: Timothy Flaherty
Abstract: Newton's method is an algorithm for finding the roots of differentiable functions, that uses iterated local linearization of a function to approximate its roots. Newton's method also extends to systems of n diferentiable functions in n variables.
In this paper, we examine the dynamics of Newton's method on system of two bivariate polynomials. We explore the generalization of Newton's method to systems of two bivariate polynomials, as well as techniques of computer visualization for the corresponding dynamics. In particular, we investigate whether the attracting cycles that arise in the dynamics of Newton's Method on certain cubic polynomials of one complex variable also arise in the case of bivariate quadratics.
► Predicting galaxy ellipticity to reduce shape noise in weak lensing research, Thomas Schuster (download paper)
Advisor: Chad Schafer
Abstract: We predict the ellipticity of galaxies from a variety of variables available through data from the Canada-France-Hawaii Lensing Survey. A survey of regression methods, including both nonparametric and tree-based methods, are applied to the prediction problem and results are discussed and compared. We present graphical methods for finding interactions between predictors. Leave- one-out cross-validation, K-fold cross-validation, and the Akaike information criterion are used to choose parameters of the models.
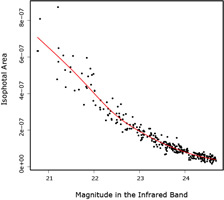
We find that projection pursuit regression performs the best on a separate test set of data. Tree-based models performed poorly due to strong linear relationships in the data.
Students
- Allen, Larry, Towson University
- Borst, Katherine, Carnegie Mellon University
- Claiborne, Brittany, Smith College
- Eagan, Nicolle, University at Buffalo
- Hauser, George, Brown University
- Kuzemchak, Kelly, Carnegie Mellon University
- Pilewski, Katherine, Boston College
- Schuster, Thomas, University of California, Berkeley
- Semsioglu, Sinem, Oberlin College
- Shahir, Munira, University of Maryland, Baltimore
- Shin, Woosub, College of the Holy Cross
- Spencer-Strong, Rebecca, Towson University
- Van Neste, Alexandra, Mount St. Mary's University
Group photo

Faculty

Tim Flaherty, Associate Teaching Professor
Project Director
E-mail: tim@andrew.cmu.edu
Wean Hall 8216
412-268-8171

Dave Handron, Associate Teaching Professor
Course: Symbolic Programming in Mathematics
Project Director
E-mail: handron@andrew.cmu.edu
Wean Hall 6214
412-268-5583

Alexei Kolesnikov, Shelly Visiting Associate Professor
Project Director
E-mail: alexei@andrew.cmu.edu

Natalie Komarov, Visiting Assistant Professor
Course: Introduction to Mathematical Finance
E-mail: nkomarov@andrew.cmu.edu
Wean Hall 6130
412-268-4380

Chad Schafer, Associate Professor
Project Director
E-mail: cschafer@cmu.edu
Baker Hall 228D
412-268-3967