► Rationally $\chi-$slice links, Kalev Martinson

Advisor:  Jonathan Simone
Abstract:  A knot in $S^3$ is called slice if it bounds a smoothly properly embedded disk in the 4-ball $B^4$. A knot is called rationally slice if it bounds a smoothly embedded disk in some rational homology 4-ball (which is a 4-dimensional manifold with the same rational homology at $B^4$). A link (which is a collection of knots tangled together) is called $\chi-$slice if it bounds a smoothly properly embedded surface in $B^4$ with no closed components and Euler characteristic 1.

The notions of rationally sliceness and $\chi-$sliceness are both generalizations of sliceness in the following way: every slice knot is rationally slice; and every $\chi-$slice knot is slice. The objective of this project is to combine these two generalizations of sliceness; we define a link to be rationally $\chi-$slice if it bounds a property embedded Euler characteristic 1 surface with no closed components in some rational homology 4-ball. We also define the rational $\chi-$concordance group, which serves as a generalization of both the rational concordance and link concordance groups which are well-known in the literature.

We then turn to showing that these new concepts are nontrivial and warrant study. To this end, we develop methods that can be used to show a given link is not rationally $\chi-$slice and use it to show that not all links are rationally $\chi-$slice. We then use geometric arguments to show that there exist infinitely many rationally $\chi-$slice links with more than one component that are not $\chi-$slice; hence the notion of rational $\chi-$sliceness contains as a proper subset all rationally slice knots and $\chi-$slice links.

► Using Lean to Teach Proof Writing, Suhas Alladaboina, Sydney Badescu, Rohan Bafna

Advisor:  Pavel Kovalev
Abstract:  We developed a Lean game using the Lean4 Game Engine that covers the first several chapters of Clive Newstead's An Infinite Descent into Pure Mathematics. This project involved creating new tactics that mimic the proof strategies presented in the textbook, helping to reduce the Lean learning curve. The game can serve as an optional supplement to help students become more comfortable with proof techniques.

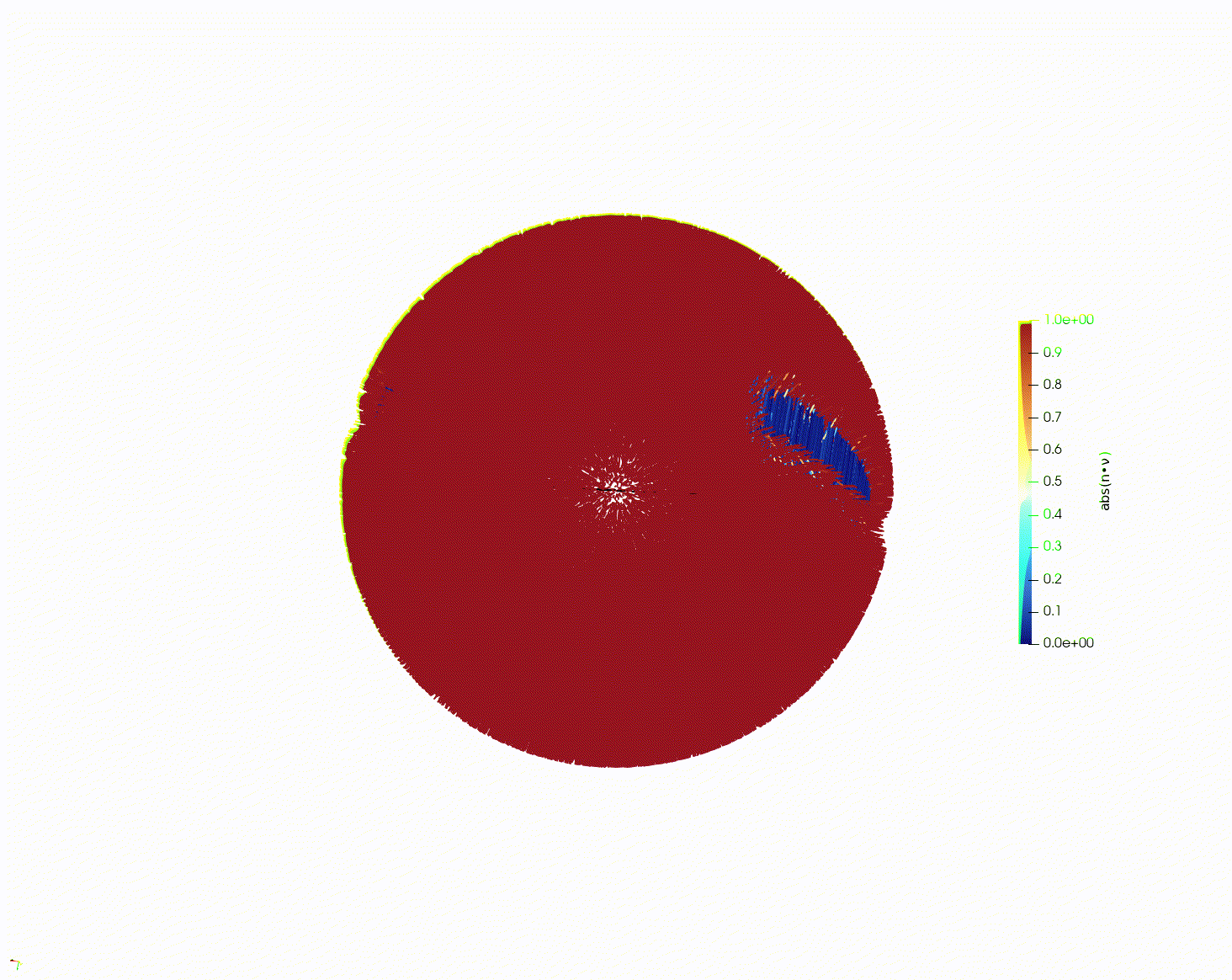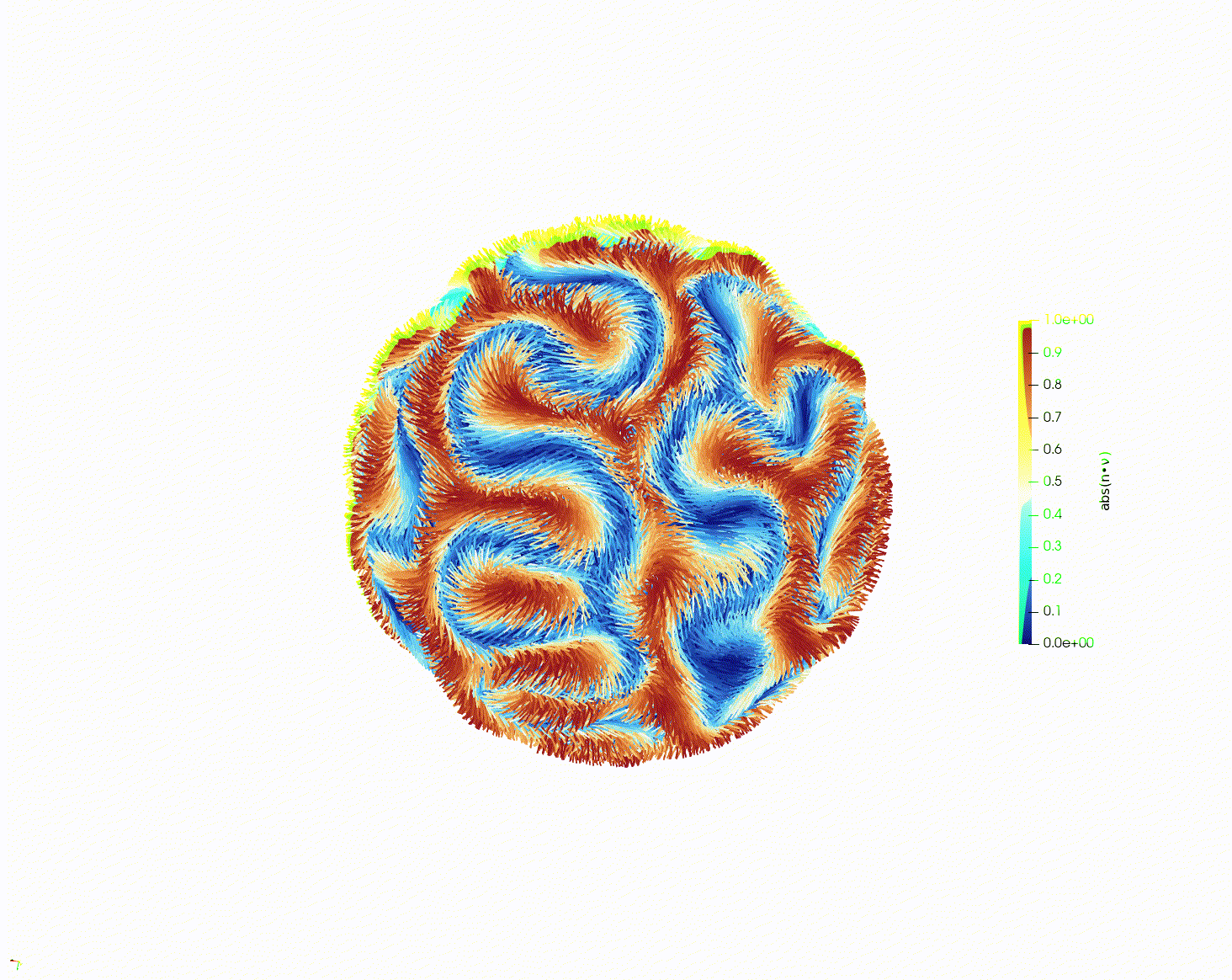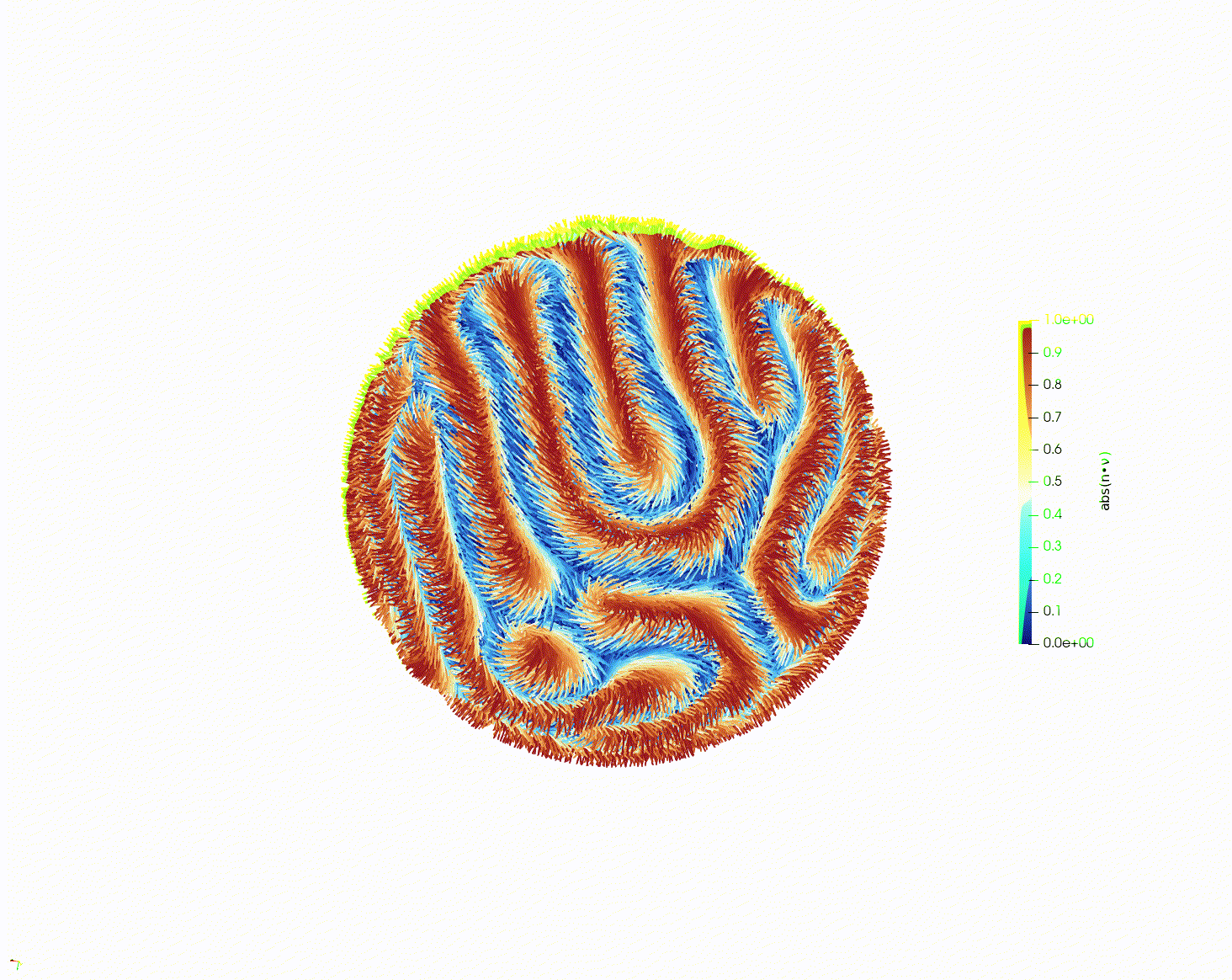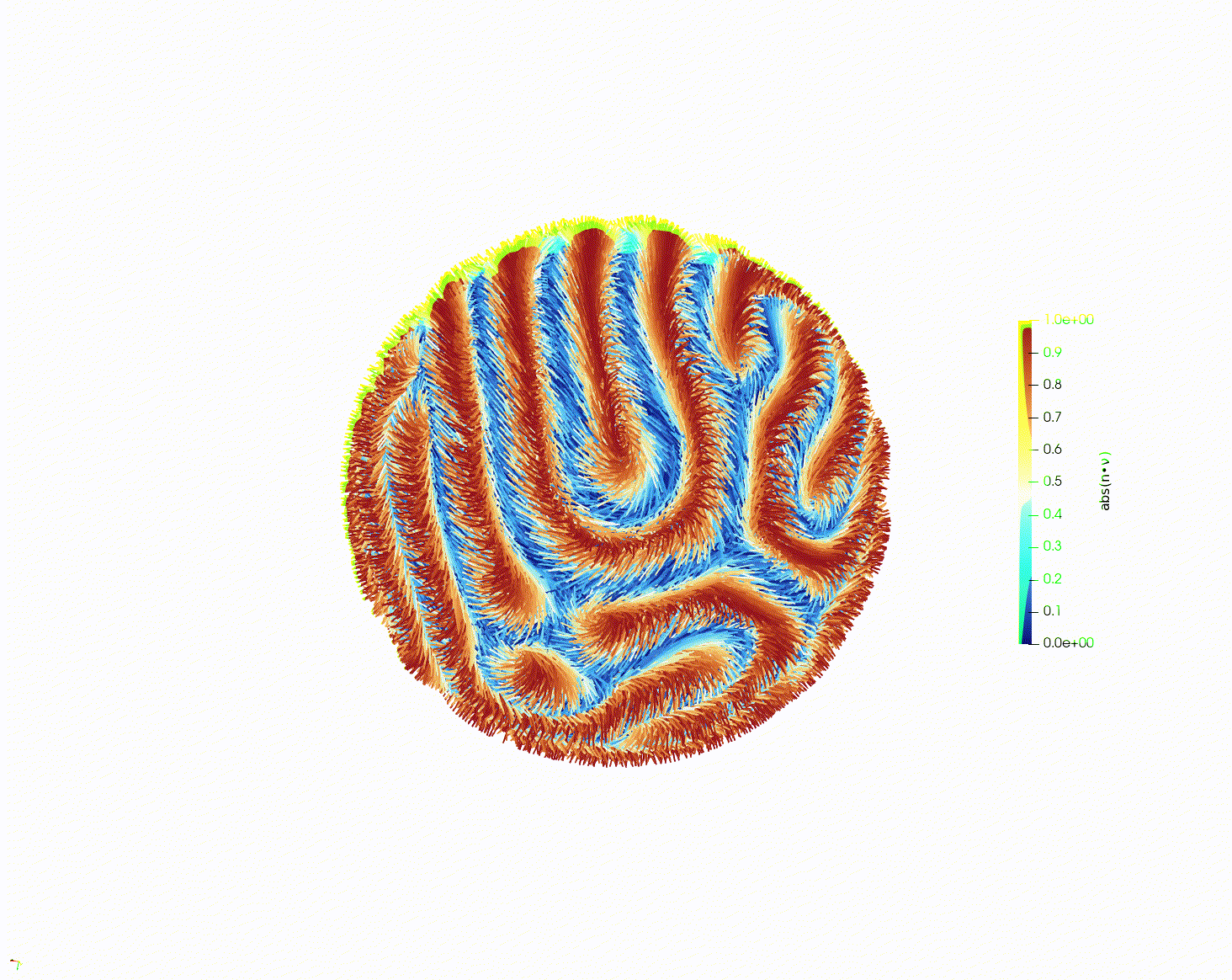
► Radio Labelings and the Moore bound, An Cao, Julian Hutchins, Orlando Luce

Advisor:  Aleyah Dawkins
Abstract:  First introduced by Hale in 1980, the frequency assignment problem (or channel assignment problem) addresses the challenge of assigning frequencies to transmitters such that interference is minimized. In 2001, Chartrand et al. formulated the radio labeling problem to model the frequency assignment for radio towers, with modern applications to cellular and satellite networks. For a simple, connected graph $G = (V (G), E(G))$, a radio labeling is a mapping $f : V (G) → Z^+$ satisfying for any distinct vertices $u$, $v$

$$|f (u) − f (v)| + d(u, v) \ge \mathrm{diam}(G) + 1,$$

where $d(u, v)$ is the distance between $u$ and $v$ in $G$ and $\mathrm{diam}(G)$ is the diameter of $G$. A graph is radio graceful if there is a radio labeling such that $f (V (G)) = \{1, . . . , |V (G)|\}$. We investigated the radio gracefulness of low-diameter graphs closely related to the Moore bound, including Moore graphs, bipartite Moore graphs, and approximate Moore graphs like $(r, g)$-cages, Erdős-Rényi polarity graphs, and McKay-Miller-Širáň graphs.

These low-diameter graphs are known to have applications in network design, particularly for high-performance networks. A necessary and sufficient condition for radio graceful bipartite graphs with diameter 3 was proved. Radio labelings of $(r, g)$-cages arising from generalized $n$-gons and Erdős-Rényi polarity graphs were found. The radio gracefulness of known $(r, g)$-cages was also considered, with the only radio graceful $(r, g)$-cages found being complete graphs and Moore graphs of girth 5 and 6.