Summer Undergraduate Applied Mathematics Institute
May 30 - July 22, 2023
Projects
► Assessing the Robustness of VBMC for Extracting Parameters in Differential Equations, Anna Rittenhouse, Grace Rojo, Alia Valentine
Advisors: Rachel Kurchin, David Offner, Jerry Wang
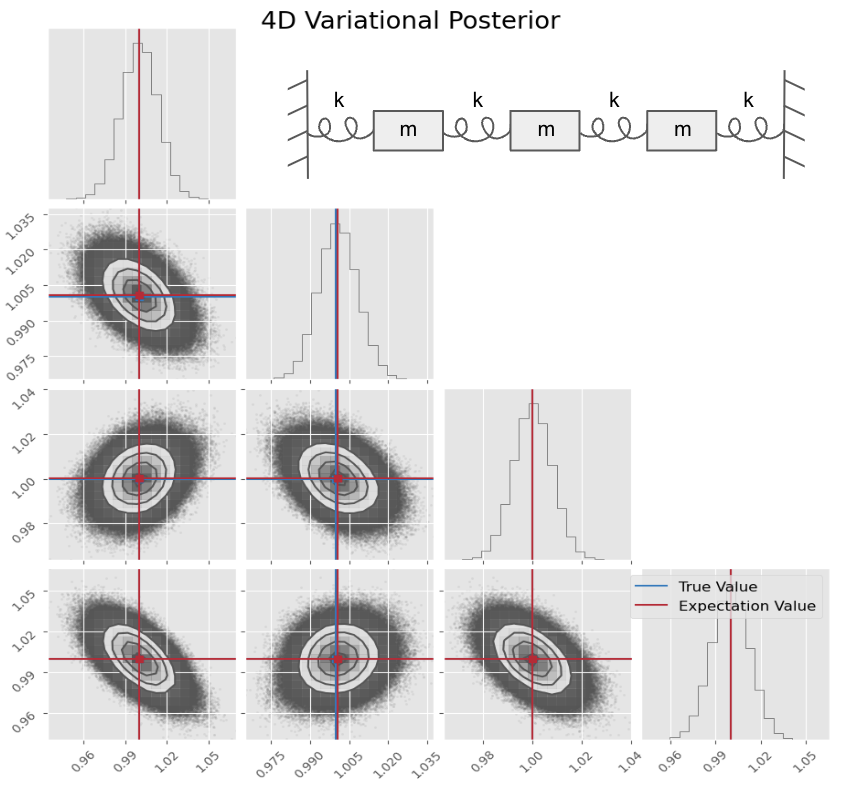
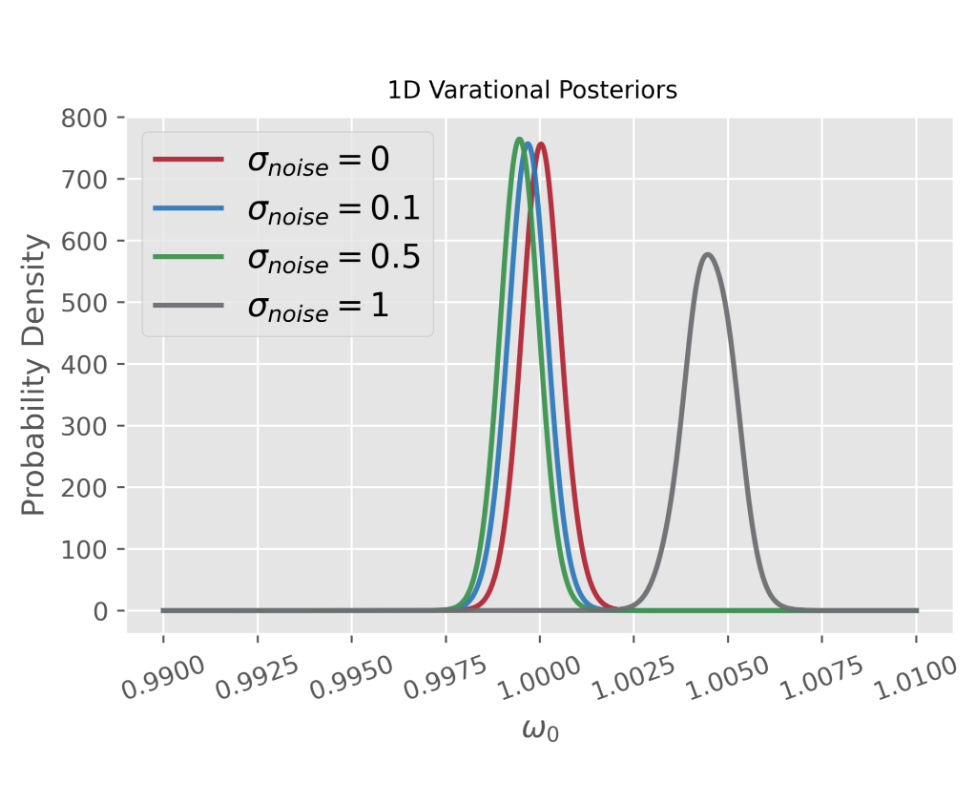
Abstract: We study a challenging problem related to parameter inference for a non-linear dynamical system of significant physical interest. In particular, we investigate a recently proposed flavor of Bayesian Monte Carlo -- Variational Bayesian Monte Carlo (VBMC) -- in the context of inferring parameters for a system of coupled anharmonic oscillators. Whereas the magnitude of the force on a harmonically oscillating mass is given by $k|x|$ (where $x$ is the distance of the mass from equilibrium and $k$ is the spring constant), we study a variation on this system where the magnitude of the force is $k|x|^a$. Though the change is a small one, all bets are off on anything resembling an analytical solution (or even an approximation) when $a\neq 1$.
► Colorings avoiding disjoint rainbow triangles, tahda queer, Cyrus Young, Wohua Zhou
Advisor: Juergen Kritschgau
Abstract: Given an edge-colored graph $G$, we denote the number of colors as $c(G)$, and the number of edges as $e(G)$. An edge-colored graph is rainbow if no two edges share the same color. A proper $mK_3$ is a vertex disjoint union of $m$ rainbow triangles. Rainbow problems have been studied extensively in the context of anti-Ramsey theory, and more recently, in the context of Tur\'{a}n problems. B. Li. et al. European J. Combin. 36 (2014) found that a graph must contain a rainbow triangle if $e(G)+c(G) \geq \binom{n}{2}+ n$. L. Li. and X. Li. Discrete Applied Mathematics 318 (2022) conjectured a lower bound on $e(G)+c(G)$ such that $G$ must contain a proper $mK_3$.
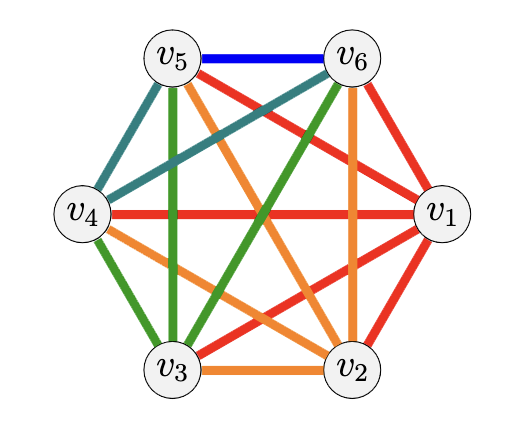
In this paper, we provide a construction that disproves the conjecture, and we introduce results that guarantee the existence of a proper $mK_3$ in general graphs and complete graphs.
► Doubling measures along sets of natural numbers: analysis meets number theory, Zoe Markman, Teresa Pollard, Joahua Zeitlin
Advisors: Theresa Anderson, Elisa Bellah
Abstract: Using a wide array of machinery from diverse fields across mathematics, we provide a construction of a measure on the real line which is doubling on all n-adic intervals for any finite list of natural number n, yet not doubling overall. In particular, we extend previous results in the area, where only two coprime numbers $n$ were allowed, by using substantially new ideas. In addition, we provide several nontrivial applications to reverse Hölder weights, $A_p$ weights, Hardy spaces, BMO and VMO function classes, and connect our results with key principles and conjectures across number theory.

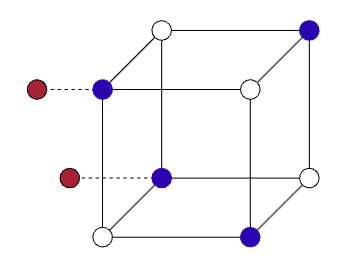
► Leaky positive semi-definite zero forcing, Ian Farish, Olivia Elias, Emrys King, Josh Kyei
Advisor: Ryan Moruzzi
Abstract: Zero forcing on a graph is an iterative graph coloring process where, starting with an initial set of blue vertices, we try to force other non-blue vertices blue according to a color change rule. The zero forcing number of a graph was first defined in 2008 by a AIM (American Institute of Mathematics) working group as a method of bounding the maximum nullity of a graph. Motivated by monitoring an electrical network, leaks are introduced into the graph hindering the ability of vertices to force. Though we lose the connection with the maximum nullity of a graph, leaks in a graph present interesting new avenues of research pertaining to the area of zero forcing. Our work involved determining the leaky forcing number of graphs for a variation of zero forcing known as positive semidefinite zero forcing.
Students
- Olivia Elias, University of Colorado
- Ian Farish, California State Polytechnic University
- Emrys King, Pomona College
- Josh Kyei, Morehouse College
- Zoe Markman, Swarthmore College
- Teresa Pollard, New York University
- tahda queer, CUNY
- Anna Rittenhouse, Clark Atlanta University
- Grace Rojo, Massachusetts Institute of Technology
- Alia Valentine, Michigan State University
- Cyrus Young, University of California, Irvine
- Joahua Zeitlin, Yale University
- Wohua Zhou, California State University, East Bay





Faculty
Theresa Anderson
Assistant Professor
E-mail: tanders2@andrew.cmu.edu
Elisa Bellah
Postdoctoral Associate
E-mail: ebellah@andrew.cmu.edu
Juergen Kritschgau
Postdoctoral Associate
Rachel Kurchin
Assistant Research Professor
E-mail: rkurchin@andrew.cmu.edu
Ryan Moruzzi
Assistant Professor
California State University, East Bay
E-mail: ryan.moruzzi@csueastbay.edu
David E. Offner
Associate Teaching Professor
E-mail: doffner@andrew.cmu.edu
Jerry Wang
Assistant Professor
E-mail: gjwang@cmu.edu