Summer Undergraduate Applied Mathematics Institute
May 31 - July 23, 2022
Projects
► Optimization in the Emerald Cloud Lab, Janiece Jackson, Layla Montemayor
Advisors: Ali Mohammed Nezhad, David Offner
Abstract: The Emerald Cloud Lab (ECL) is a first-of-its-kind research lab that allows scientists to design and submit experiments from anywhere in the world, executed by operators on instruments at ECL's facility in California. For its success, it is critical that experiments are completed in a timely manner. This project uses the discrete time simulation software Arena to build a model of ECL's operations, incorporating historical data from the lab. This tool allows us to analyze the number of jobs completed and queue time under different assumptions on staffing, instrumentation, and type and frequency of requests from customers.
Ultimately, we can locate bottlenecks in the lab's operations and recommend optimal levels of staffing and instrumentation for ECL to successfully satisfy customer demand.
► Cycle decompositions of Cartesian products of cycles, Moriah Aberle, Sarah Gold, Rivkah Moshe
Advisor: David Offner
Abstract: We say a graph $H$ decomposes a graph $G$ if there exists a partition of the edges of $G$ into subgraphs isomorphic to $H$.

In this project, we seek to characterize necessary and sufficient conditions for a cycle of length $k$, denoted $C_k$, to decompose the Cartesian product of two cycles $C_m ~\square~ C_n$.
The two main results of this project are:
- If $m$ is a multiple of 3, then the Cartesian product of a cycle $C_m$ and any other cycle can be decomposed into 3 cycles of equal length. This extends work of Kotzig, who proved in 1973 that the Cartesian product of two cycles can always be decomposed into two cycles of equal length.
- If $k$, $m$, and $n$ are multiples of four, and $k$ divides $mn$, then $C_k$ decomposes $C_{m} ~\square~ C_{n}$.
► Portfolio optimization, Taj Allemby, David Baron, Michael Eddy
Advisors: Bill Hrusa, Aris Winger
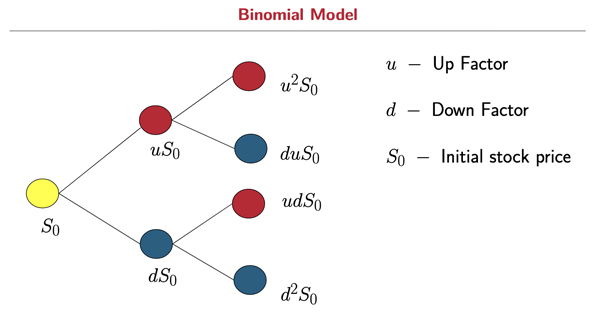
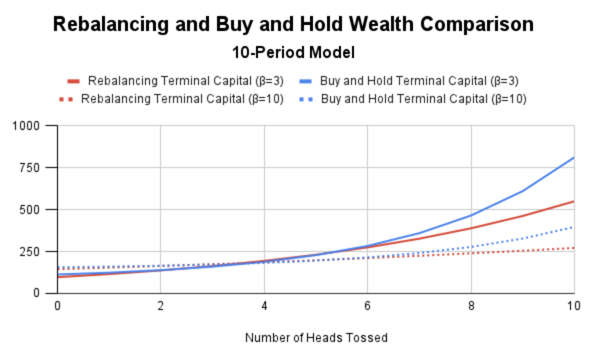
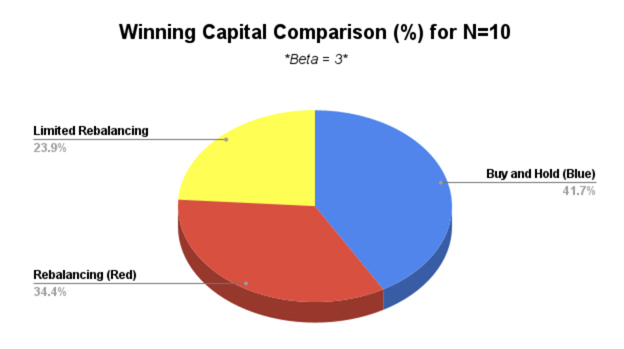
Abstract: When participating in financial markets, investors are often posed with the question of where, when, and how to invest their capital. In an effort to explore this matter, this project seeks to understand how to optimize portfolio allocation under historically aligned market conditions. To achieve this, we implemented the binomial asset-pricing model as we surveyed and compared three commonly practiced trading strategies: Rebalancing every period, Limited Rebalancing, and Buy and Hold. Incorporating utility functions to represent an investor's risk aversion, we sought to maximize the expected utility of our terminal capital. In doing so, we derived formulas representing an investor's level of wealth under optimal investment for each of the three strategies. We then found relations between the capitals for each of the strategies, leading to a conjecture concerning the dependence of the optimal portfolio on various parameters.
► The $Z_q$-forcing number for some graph families, Jorge Blanco, Stephanie Einstein, Caleb Hostetler, Daniel Ogbe
Advisor: Juergen Kritschgau
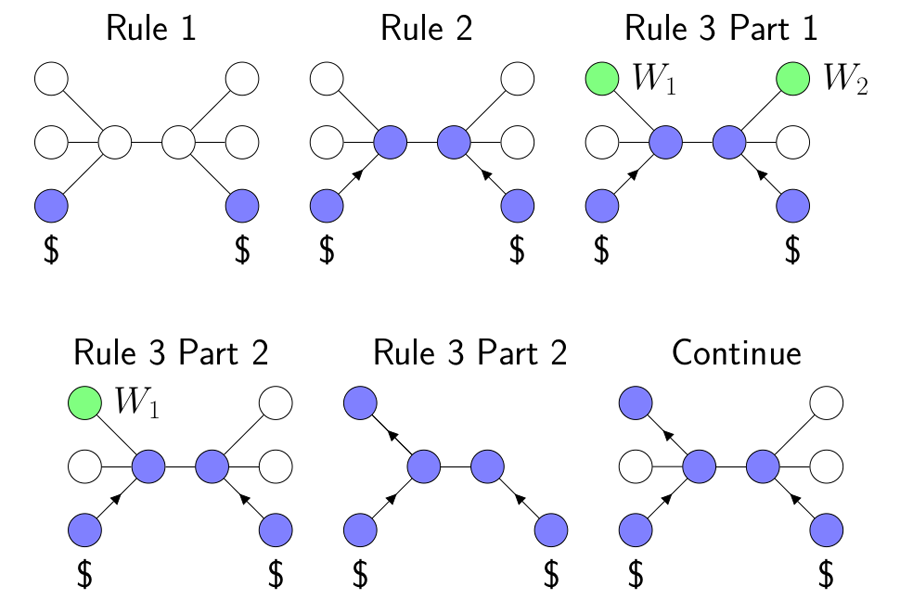
Abstract: The zero forcing game was introduced as a combinatorial bound on the maximum nullity taken over the set of real symmetric matrices that respect the pattern of an underlying graph.
The $Z_q$-forcing game is an analog to the standard zero forcing game which incorporates inertia restrictions on the set of matrices associated with a graph. This work proves an upper bound on the $Z_q$-forcing number for trees with $q\geq 3$. Furthermore, we consider the $Z_q$-forcing number for the $k$-corona of a cycle on $n$ vertices.
We focus on developing game theoretic proofs of upper and lower bound.
Students
- Moriah Aberle, Denison College
- Taj Allemby, Morehouse College
- David Baron, Williams College
- Jorge Blanco, Yale University
- Michael Eddy, Swarthmore College
- Stephanie Einstein, Mt. Holyoke College

- Sarah Gold, Haverford College
- Caleb Hostetler, Eastern Mennonite University
- Janiece Jackson, Clemson University
- Layla Montemayor, University of Nebraska
- Rivkah Moshe, Boston University
- Daniel Ogbe, MIT











