Projects

► Pricing Exotic Options using Pricing Engines, Laila Ali, Taj Allamby, Mika Campbell, Vanessa Wu

Advisors: Bill Hrusa, Ben Weber
Abstract: The COVID-19 pandemic has resulted in millions of casualties worldwide, global shutdowns, and the advent of a "virtual reality". To hinder spread of the virus, eliminate casualties, and enable a return to a "normal" way of life, pharmaceutical companies have developed vaccines.

Most of these companies are publicly traded, leading to exciting opportunities for investors. This project looks at the process and equations underlying investment decisions as they relate to well-known biotech companies Pfizer and Moderna. The theory and application of the Black-Scholes Formula, multi period binomial models, and pricing techniques for plain vanilla and exotic options are explored in the context of Pfizer and Moderna stock.

► Path and cycle decompositions of hypercube graphs, Josue Antonio, Hunter Loftis, Sean O'Connor

Advisor: David Offner
Abstract: A graph $H$ decomposes a graph $G$ if the edge set of $G$ can be partitioned into edge-disjoint subgraphs isomorphic to $H$. We consider decompositions of the $n$-dimensional hypercube $Q_n$ into paths and cycles. A conjecture by Erde (2014) asserts that if $n$ is even, then a path of length $\ell$ decomposes $Q_n$ if the necessary conditions that $\ell < 2^n$ and $\ell$ divides the number of edges of $Q_n$.

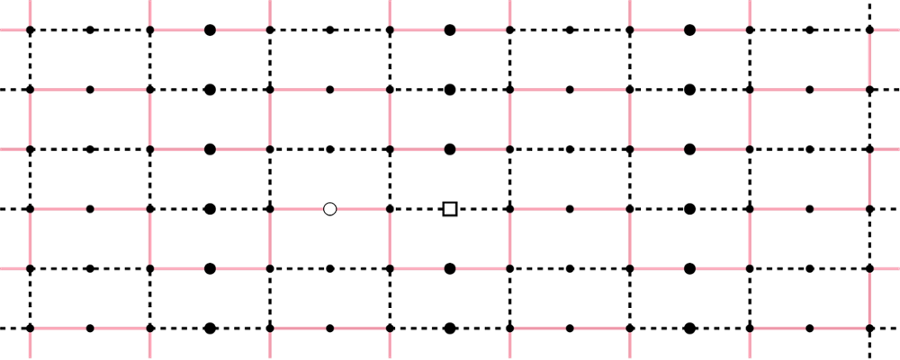
Offner et al. (2021) proved, among other results, that if $n$ is the sum of at most two powers of $2$, then the cycle with the largest length divisible by $n$ while still satisfying the necessary conditions provided by Erde decomposes $Q_n$. We improved this result to the case of $n$ being the sum of at most three powers of $2$, and strengthened other results of Offner et. al.

► Fundamental sets for hypercube graphs, Stanley Chen, Mackenzie Maude, Elise VerSchneider

Advisor: David Offner
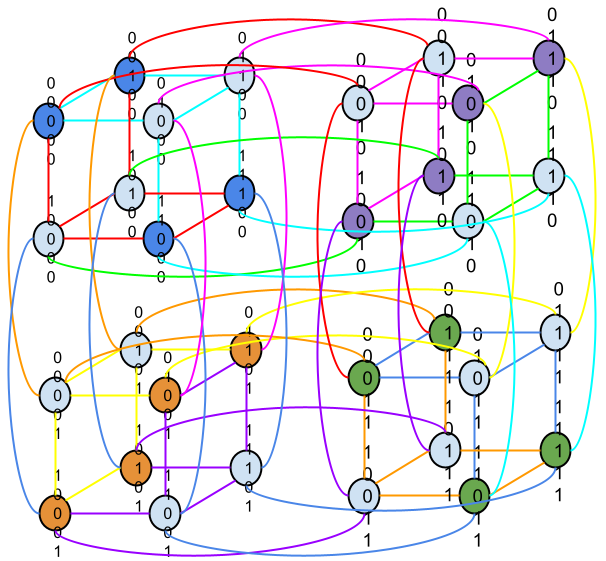
Abstract: Let $Q_n$ denote the $n$-dimensional hypercube graph, and $Aut(Q_n)$ denote the set of automorphisms on $Q_n$. A subset $T$ of the edges of $Q_n$ is a fundamental set if there is a subgroup $S$ of $Aut(Q_n)$ such that each edge in $Q_n$ is the image of $T$ under exactly one automorphism in $S$. In our research, we give inductive strategies for generating fundamental sets for larger hypercube graphs from fundamental sets for smaller ones. As corollaries, we prove that, among other graphs, various trees, paths and matchings are fundamental sets for hypercubes.

► Some limiting problems in utility maximization, Nicholas Grabill, Emma Hu

Advisor: Bill Hrusa
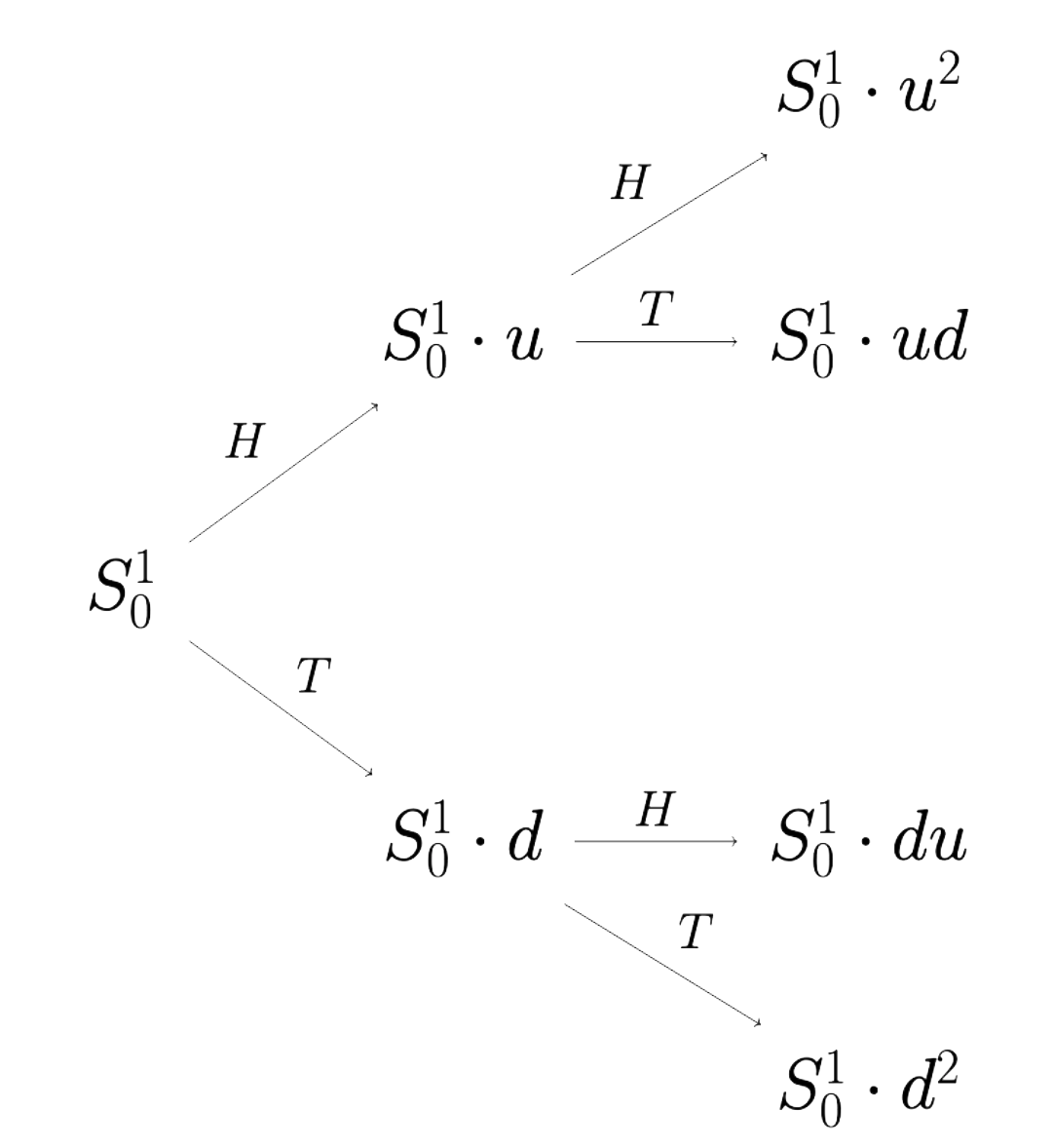
Abstract: We consider limiting cases of utility maximazation in binomial stock pricing models. We consider one-period models with $n$ independent and identically distributed stocks and also $n$-period models with one stock. In both situations we're interested in letting $n\rightarrow\infty$. In all cases there is a single-period risk-free interest rate $r$. The up factor $u$ and the down factor $d$ for the stock are constant and satisfy $0<d<1+r<u$. The movement of the stock price from one period to the next is determined by flipping a coin: when a head occurs, the stock price is multiplied by $u$ and for a tail the stock price is multiplied by $d$. In the multii-period case we we employ a buy and hold strategy. We consider most of the standard utility functions.

► Influence of compensation schemes on investor behavior, Dashon Jones, Jacob Quintero

Advisors: Bill Hrusa, Aris Winger
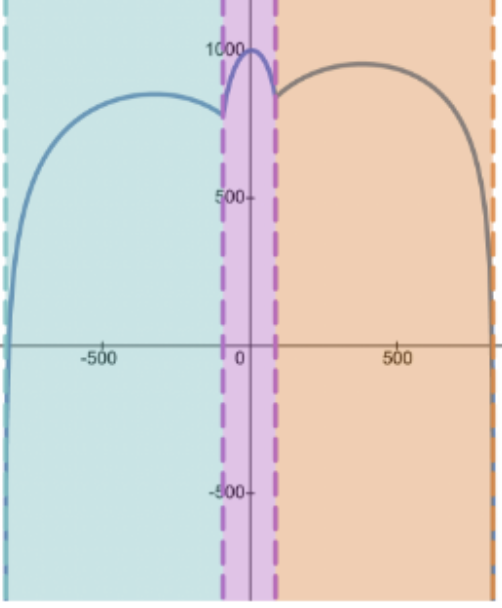
Abstract: We analyze how investors will react to compensation schemes by maximizing the expected utility in the one-period binomial, multi-period binomial, and Black-Scholes models. We prove the existence of multiple local maxima in an interval for some cases. It can happen that small changes in the parameters result in the absolute max switching from one local max to a different one.