Selected Papers
Background Modeling for Double Higgs Boson Production: Density Ratios and Optimal Transport
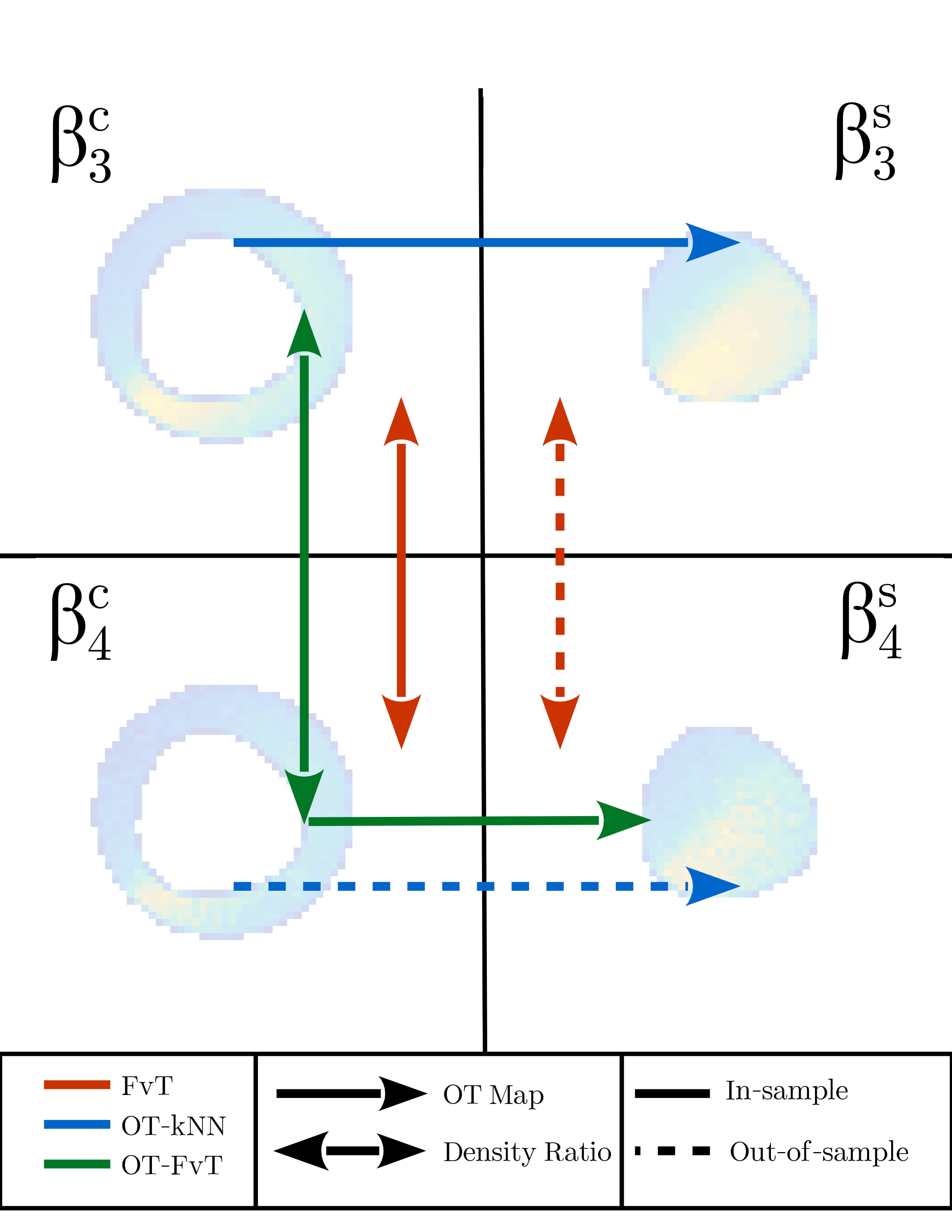
Most searches of new phenomena in high-energy physics are performed using a classifier-based test in a high-dimensional space. To train the classifier, one needs samples of both signal and background events. However, there are many situations, such as the search for the production of pairs of Higgs bosons, where no reliable simulators of background events are available. In this work, we investigate ways of obtaining data-driven background estimates by solving a transfer learning problem from a nearby signal-free data sample to the sample of interest. We propose doing this using optimal transport, a way of moving probability mass between distributions, and compare the new approach to an existing classifier-based domain adaptation method. We find that both approaches produce high-quality data-driven background estimates and that the two approaches can serve as cross-checks of each other due to the complementarity of their underlying assumptions.
To appear in the Annals of Applied Statistics.
Classification under Nuisance Parameters and Generalized Label Shift in Likelihood-Free Inference
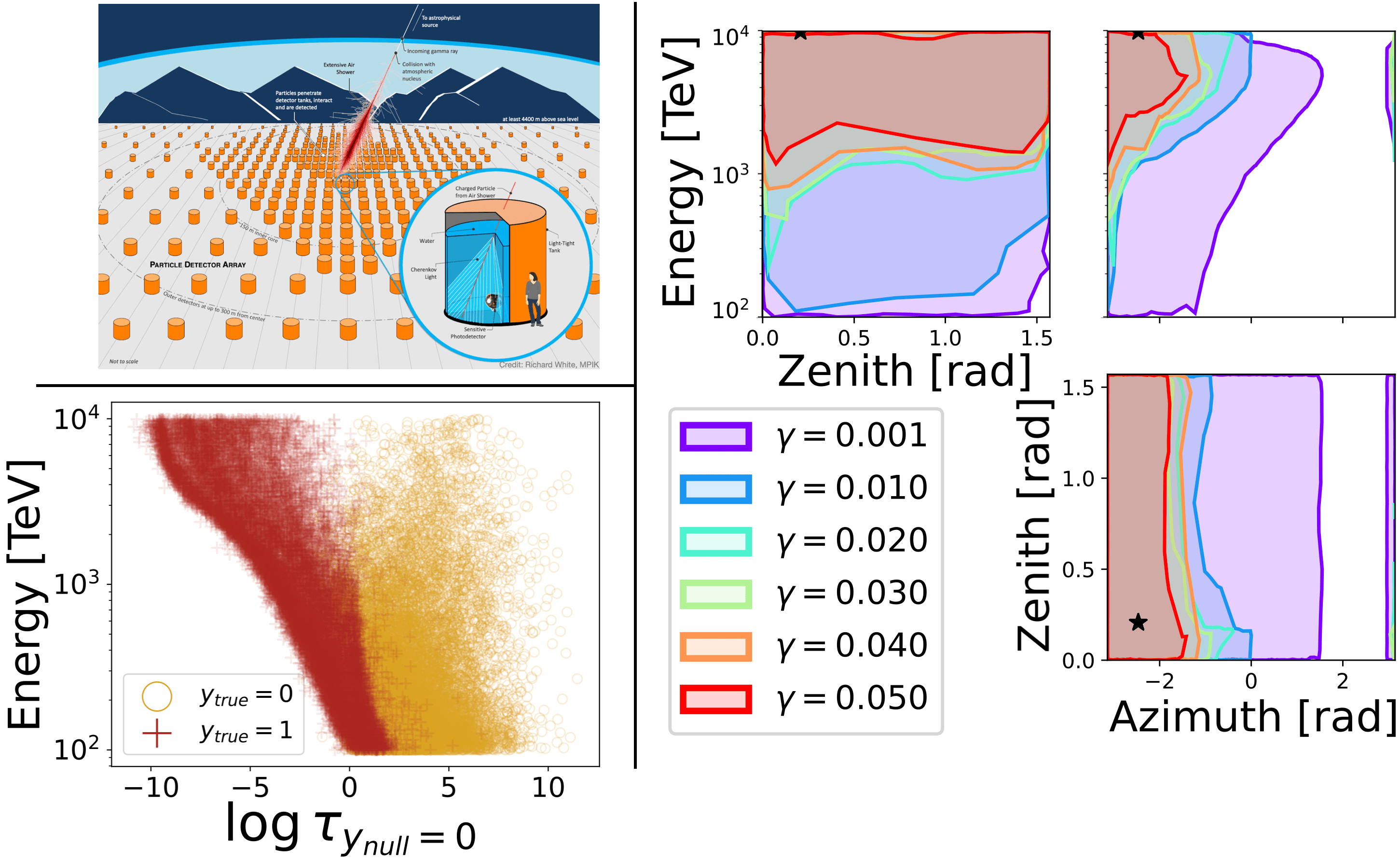
An open scientific challenge is how to classify events with reliable measures of uncertainty, when we have a mechanistic model of the data-generating process but the distribution over both labels and latent nuisance parameters is different between train and target data. Here we introduces a novel approach to classification under nuisance parameters and generalized label shift, which returns valid prediction sets while maintaining high power. We demonstrate our method on applications in biology and astroparticle physics.
Proceedings of the Forty-First International Conference on Machine Learning (ICML 2024), PMLR 235, 2024.
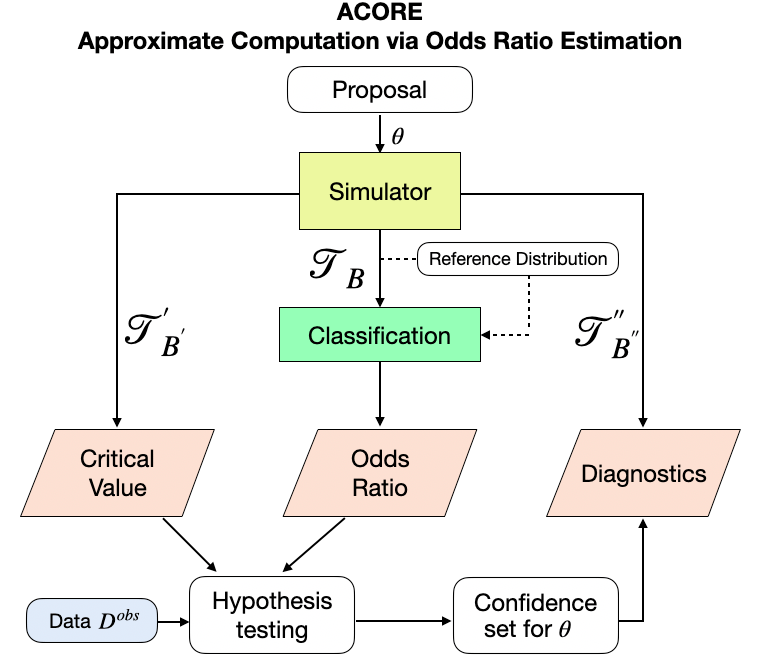
Confidence Sets and Hypothesis Testing in a Likelihood-Free Inference Setting
Parameter estimation, statistical tests and confidence sets are the cornerstones of classical statistics that allow scientists to make inferences about the underlying process that generated the observed data. A key question is whether one can still construct hypothesis tests and confidence sets with proper coverage and high power in a so-called likelihood-free inference (LFI) setting; that is, a setting where the likelihood is not explicitly known but one can forward-simulate observable data according to a stochastic model. We present ACORE, a frequentist approach to LFI that first formulates the classical likelihood ratio test (LRT) as a parametrized classification problem, and then uses the equivalence of tests and confidence sets to build confidence regions for parameters of interest. We also present a goodness-of-fit procedure for checking whether the constructed tests and confidence regions are valid.
Proceedings of the Thirty-Seventh International Conference on Machine Learning (ICML 2020), PMLR 119:2323-2334, 2020
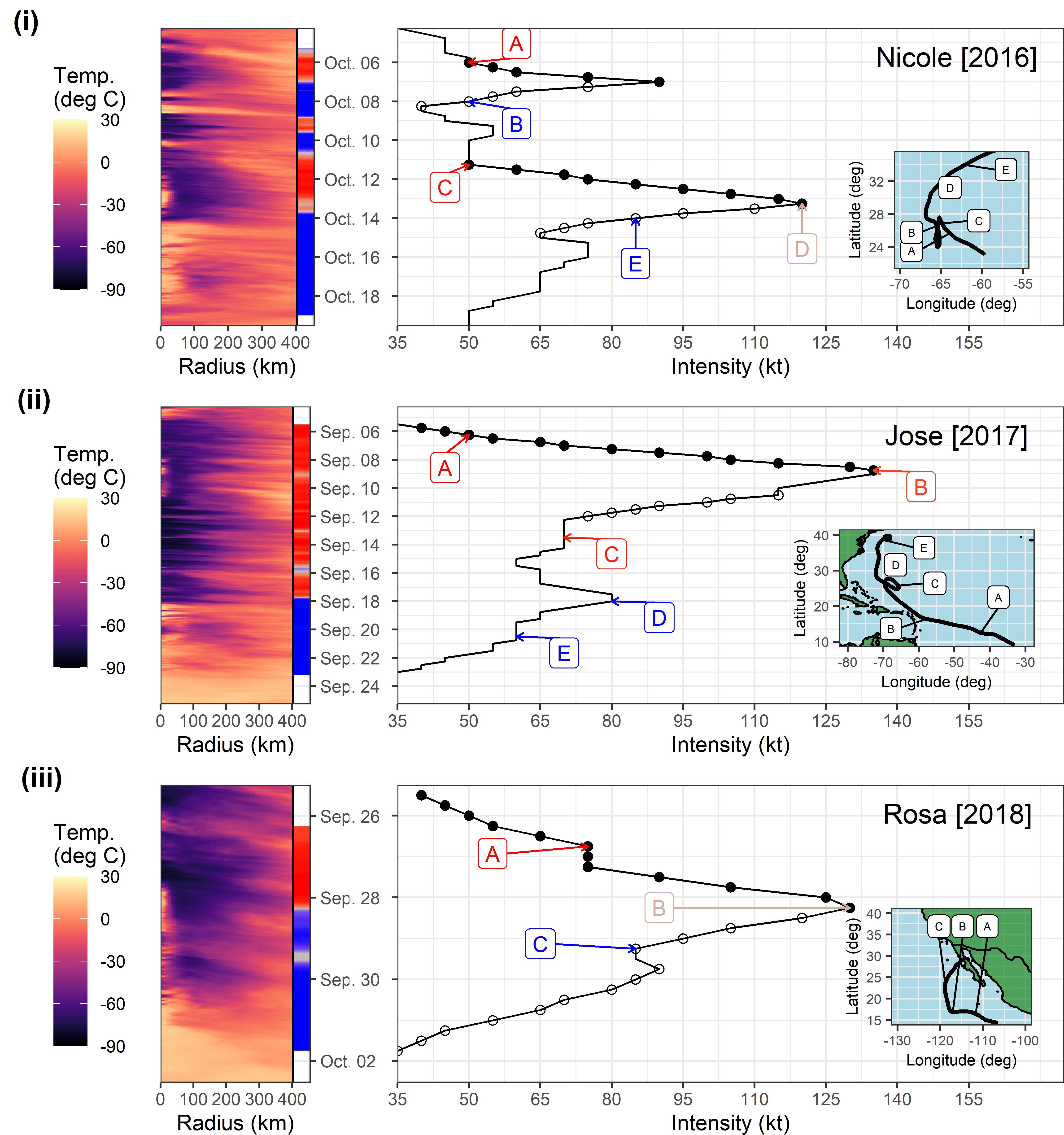
Detecting distributional differences in labeled sequence data with application to tropical cyclone satellite imagery
Selected for "The Best of AOAS" invited paper session at JSM 2023
Scientists are increasingly leveraging machine learning methods, such as prediction algorithms and neural density estimators, for parameter inference in simulator-based inference (SBI) settings. These approaches can however lead to biased parameter estimates and overly confident region estimates, even if the posterior is well-estimated and the labeled data have the same distribution as the target distribution. This paper presents WALDO, a novel method to construct confidence regions with finite-sample local validity by leveraging prediction algorithms or posterior estimators that are currently widely adopted in SBI. We apply our method to a recent high-energy physics problem, where prediction with deep neural networks has previously led to estimates with prediction bias. We also illustrate how our approach can correct overly confident posterior regions computed with normalizing flows.
Annals of Applied Statistics 17(2):1260--1284, June 2023
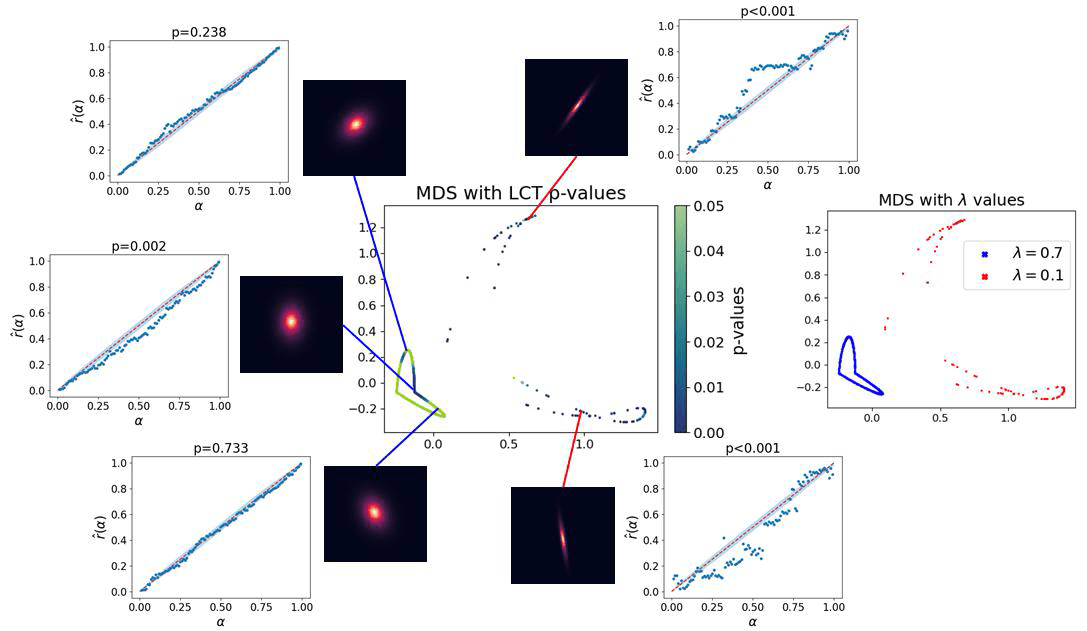
Diagnostics for Conditional Density Models and Bayesian Inference Algorithms
There has been growing interest in the AI community for precise uncertainty quantification. Conditional density models f(y|x), where x represents potentially high-dimensional features, are an integral part of uncertainty quantification in prediction and Bayesian inference. However, it is challenging to assess conditional density estimates and gain insight into modes of failure. In this work, we present rigorous and easy-to-interpret diagnostic tools that can identify, locate, and interpret the nature of statistically significant discrepancies over the entire feature space. We demonstrate the effectiveness of our procedures through a simulated experiment and applications to prediction and parameter inference for image data.
Proceedings of the Thirty-Seventh Conference on Uncertainty in Artificial Intelligence (UAI 2021). PMLR 161:1830-1840, 2021
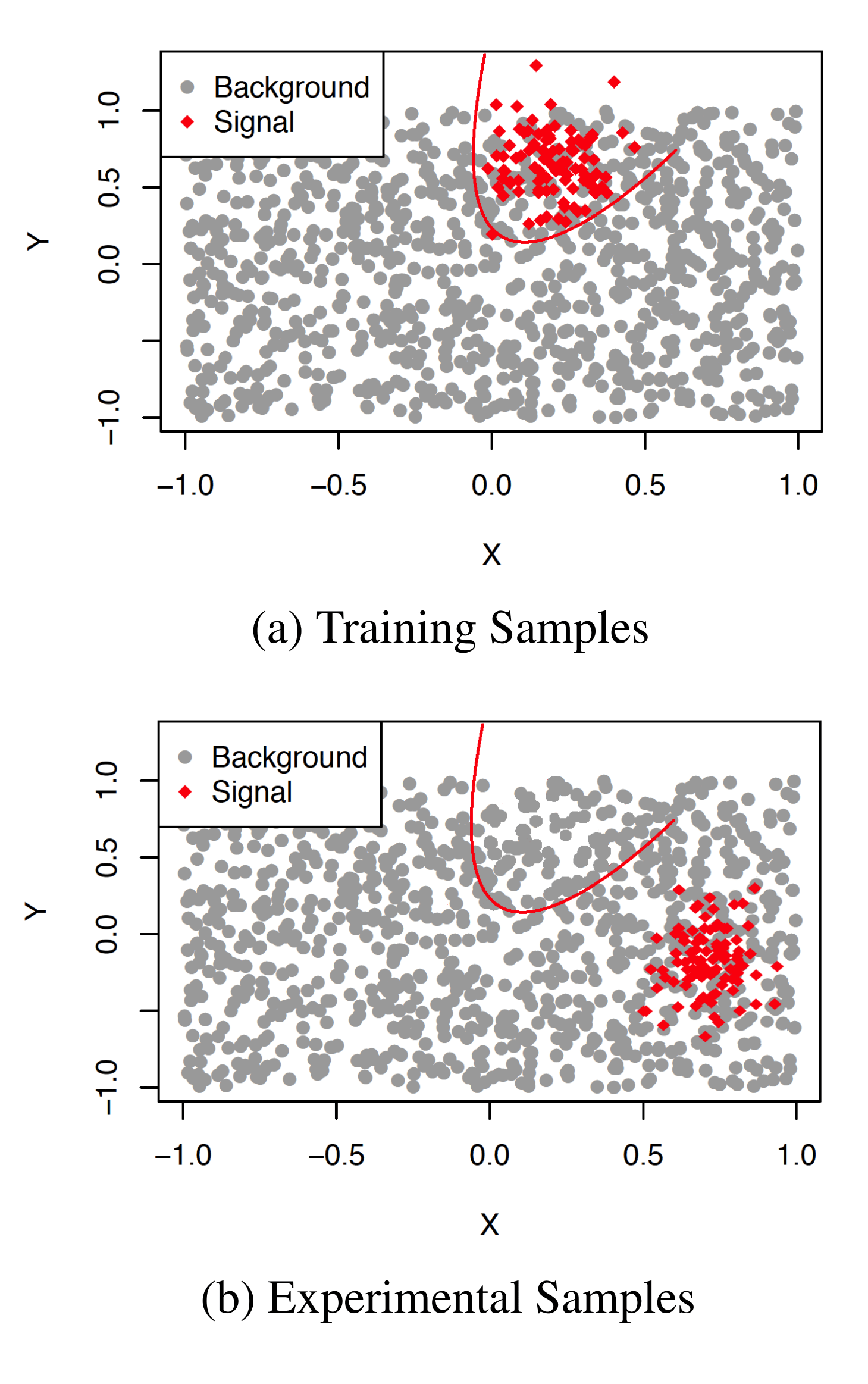
Model-independent detection of new physics signals using interpretable SemiSupervised classifier tests
Most searches for new signals in high-energy physics are optimized to look for specific deviations from the Standard Model of particle physics. While these searches can cover a wide range of possible signal hypotheses, they may not have sensitivity for unexpected or unknown new physics signals. In this work, we frame the problem of finding new physics signals as a collective anomaly detection problem and propose a way to search for high-dimensional new signals in a model-agnostic way using a semi-supervised classifier. We investigate various ways to perform a statistical hypothesis test using the classifier and propose ways to interpret the potential new signal detected using the test. We investigate the performance of the methods on a data set related to the search for the Higgs boson at the Large Hadron Collider at CERN. We demonstrate that the model-agnostic tests are competitive with the classical model-dependent methods for a known signal but have much higher sensitivity for an unexpected signal.
Annals of Applied Statistics 17(4):2759--2795, 2023
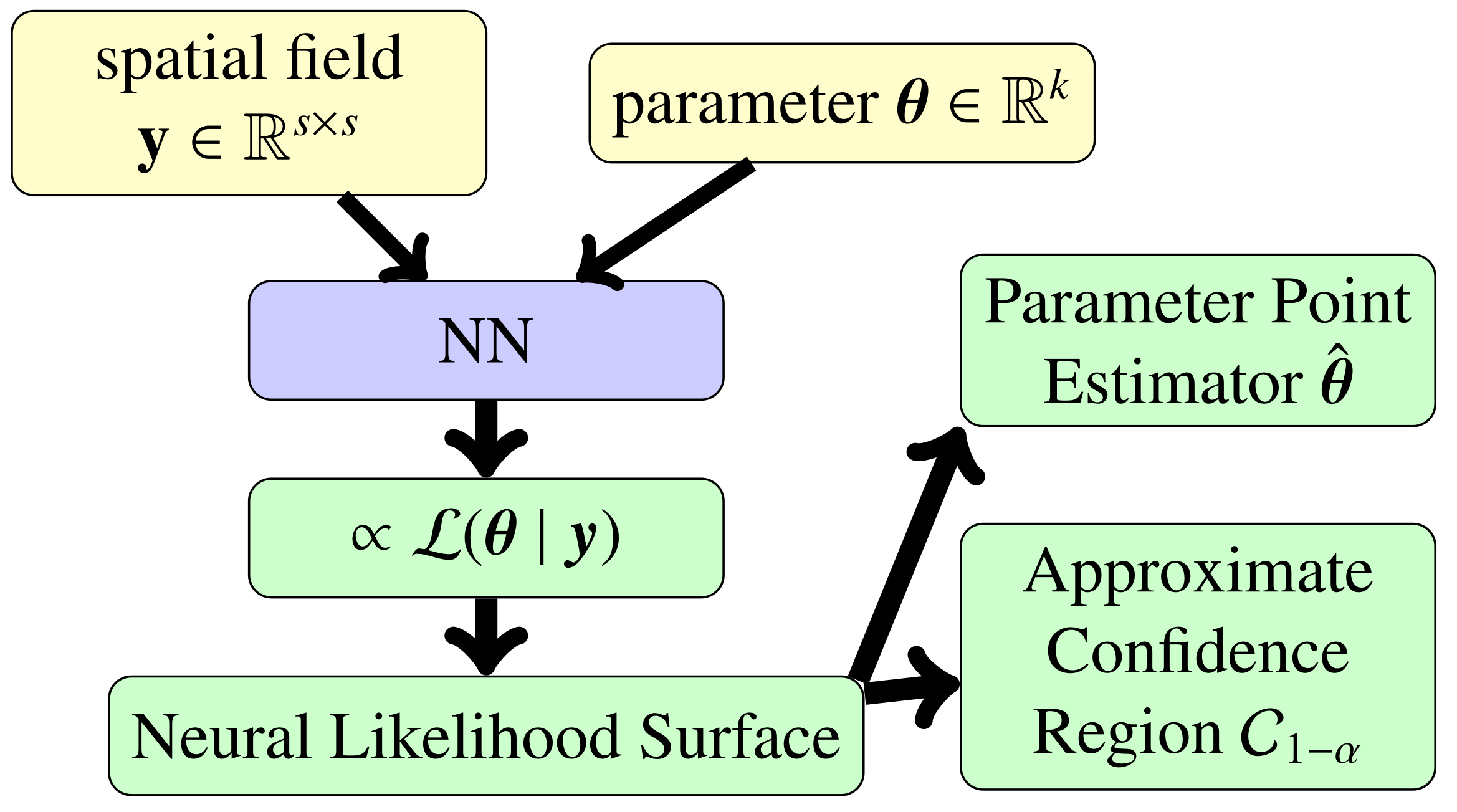
Neural Likelihood Surfaces for Spatial Processes with Computationally Intensive or Intractable Likelihoods
Winner of the ASA ENVR 2024 Student Paper Competition
For many models used in spatial statistics, parametric inference is challenging because the likelihood functions of these models are slow to evaluate or wholly intractable. In this work, we propose using convolutional neural networks to learn the likelihood function of a spatial process. Using only simulations from the model, the method enables learning a neural surrogate of the underlying, otherwise intractable likelihood function. We demonstrate the accuracy of the learned neural likelihood in a setting where the true likelihood can be computed and then proceed to learn the likelihood function of an intractable process used to model spatial extreme values. In addition to being more accurate than previous likelihood approximations, the trained neural likelihood is amortized which makes it much faster to evaluate than traditional methods in settings where the same spatial inference problem needs to be solved repeatedly.
To appear in Spatial Statistics.
Objective Frequentist Uncertainty Quantification for Atmospheric CO2 Retrievals
Remote sensing satellites observe the Earth's atmosphere from space. These observations contain only indirect information about atmospheric quantities of interest which need to be inferred from the data by solving an ill-posed inverse problem. In this work, we study the problem of estimating atmospheric carbon dioxide (CO2) concentrations from space using the OCO-2 satellite. We are specifically interested in assigning an uncertainty on the estimated CO2 concentration. We demonstrate that the reliability of existing CO2 uncertainty quantification methods is affected by biases originating from the regularization of the inverse problem. We then propose a new optimization-based uncertainty quantification technique that is designed to provide well-calibrated confidence intervals on the CO2 concentration and use a simulation study to demonstrate the reliability of these uncertainties. We also develop a principled framework to incorporate additional observational information to reduce the size of the uncertainties.
SIAM/ASA Journal on Uncertainty Quantification 10(3):827--859, 2022
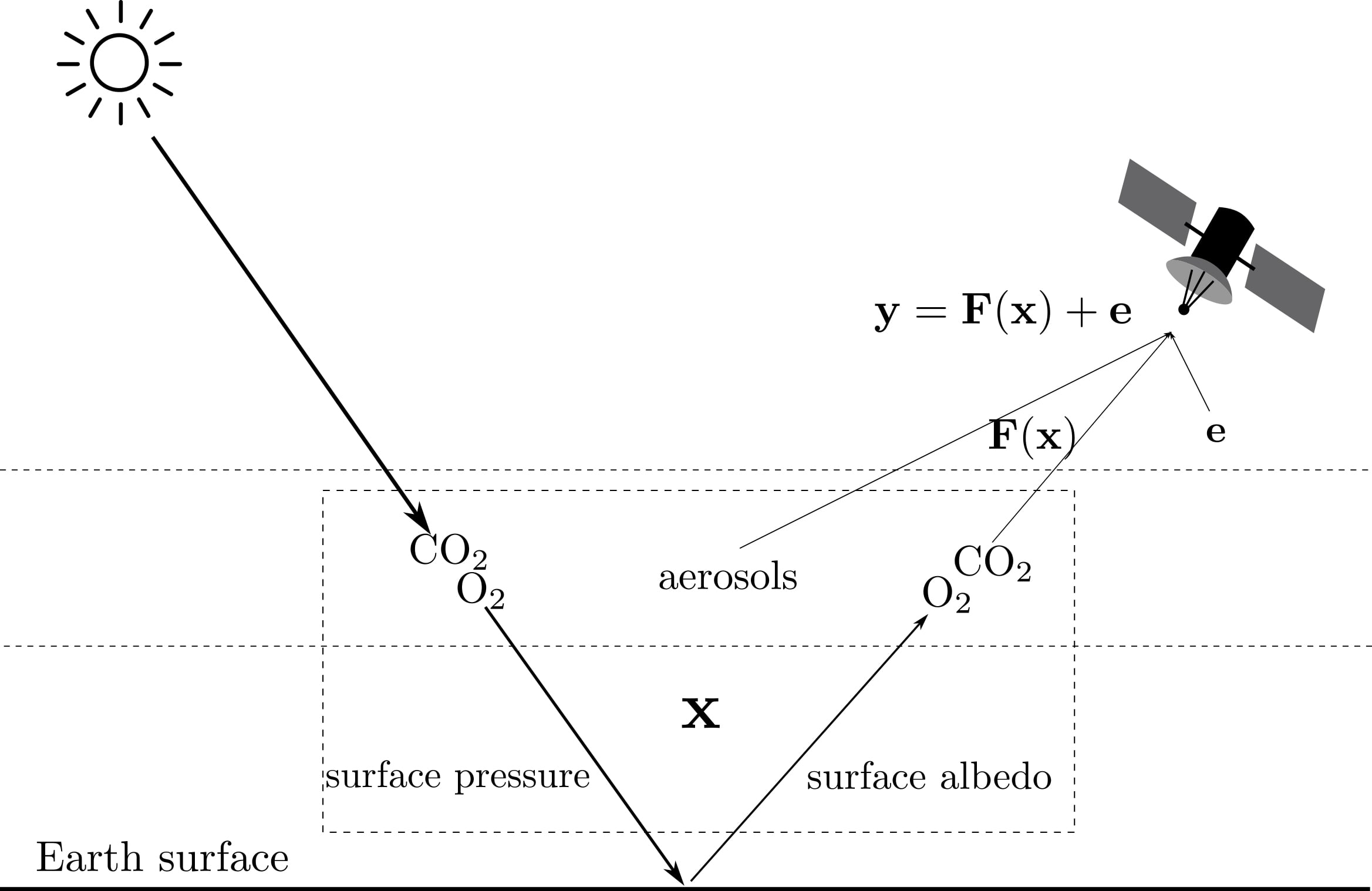
Simulator-Based Inference with WALDO: Confidence Regions by Leveraging Prediction Algorithms and Posterior Estimators for Inverse Problems
Finalist at the ASA SPES and Q&P Student Paper Competition
Scientists are increasingly leveraging machine learning methods, such as prediction algorithms and neural density estimators, for parameter inference in simulator-based inference (SBI) settings. These approaches can however lead to biased parameter estimates and overly confident region estimates, even if the posterior is well-estimated and the labeled data have the same distribution as the target distribution. This paper presents WALDO, a novel method to construct confidence regions with finite-sample local validity by leveraging prediction algorithms or posterior estimators that are currently widely adopted in SBI. We apply our method to a recent high-energy physics problem, where prediction with deep neural networks has previously led to estimates with prediction bias. We also illustrate how our approach can correct overly confident posterior regions computed with normalizing flows.
Proceedings of the Twenty-Sixth International Conference on Artificial Intelligence and Statistics (AISTATS 2023), PMLR 206:2960-2974, 2023
Spatiotemporal local interpolation of global ocean heat transport using Argo floats: A debiased latent Gaussian process approach
The world ocean plays a key role in redistributing heat in the climate system and hence in regulating Earth's climate. Due to the scarcity of subsurface data, it is nontrivial to produce observational estimates of this ocean heat transport. In this work, we use state-of-the-art techniques from spatio-temporal statistics to develop a comprehensive framework for mapping ocean heat transport globally using data from the Argo array of profiling floats. We develop a two-stage mapping procedure to handle the fact that Argo observes ocean currents only indirectly. This approach provides data-driven global ocean heat transport fields that vary in both space and time and can provide crucial insights into ocean climate. The accuracy of these estimates is validated by generating synthetic observations from a high-resolution satellite data product at the ocean surface.
Annals of Applied Statistics 17(2):1491--1520, 2023
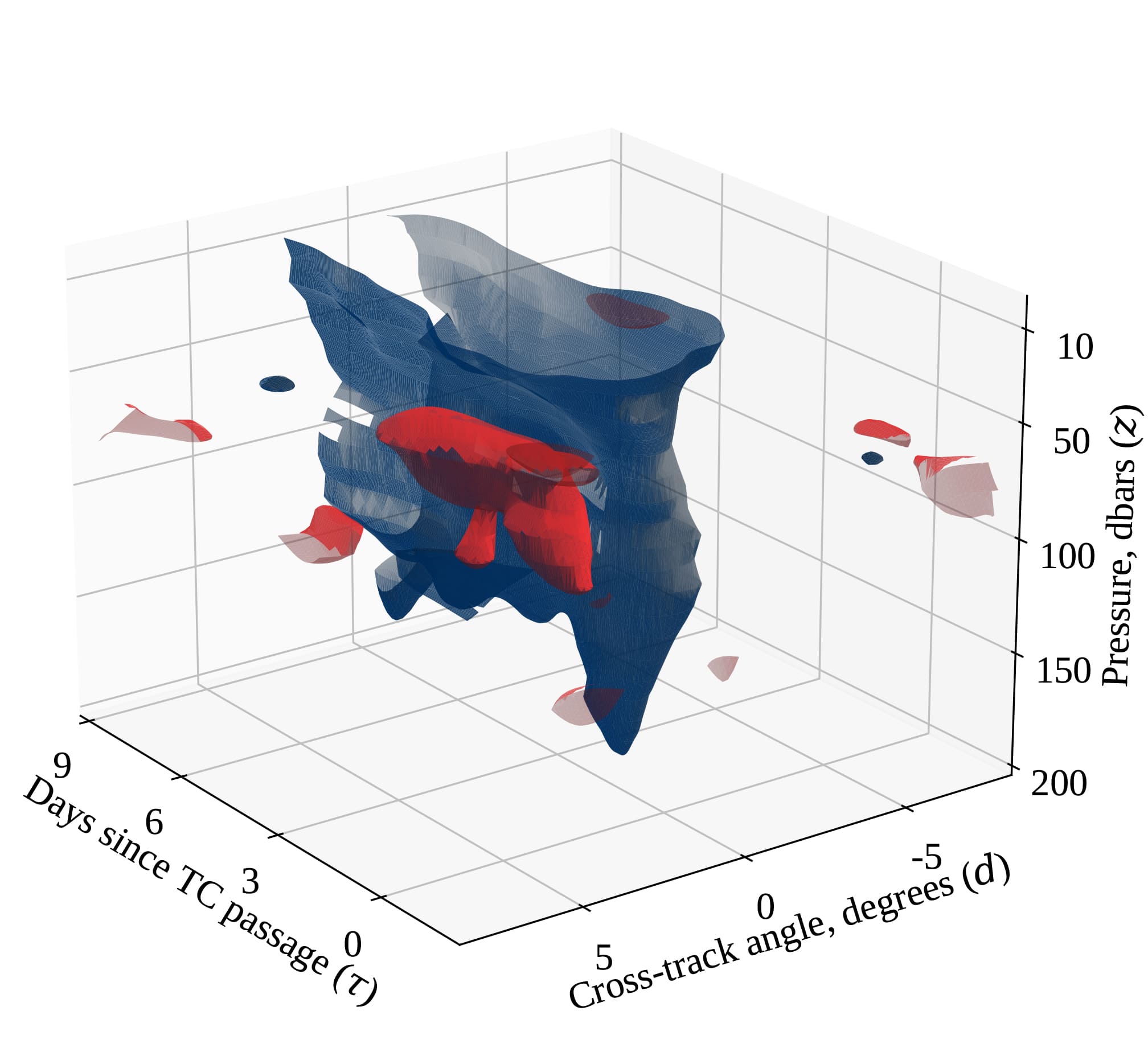
Spatio-temporal methods for estimating subsurface ocean thermal response to tropical cyclones
As tropical cyclones (TCs) move across the ocean, they leave behind a wake of anomalous ocean temperatures caused by their various interactions with the water column. This TC wake is relatively easy to characterize at the ocean surface using satellite data but observing how TCs affect the subsurface ocean is much more challenging. In this work, we use vertical temperature profiles from the Argo array of autonomous floats to characterize how TCs impact the subsurface ocean. Even though Argo is not designed to resolve spatio-temporal scales relevant for TCs, we demonstrate that with careful statistical modeling, it is possible to extract the average impact of TCs as a function of space, time and depth from the Argo observations. These estimates may improve our understanding of the role of TCs in the global climate system. In addition, the methodology can be adapted to estimate other previously unresolved transient signals using the Argo observations.
To appear in Advances in Statistical Climatology, Meteorology and Oceanography.
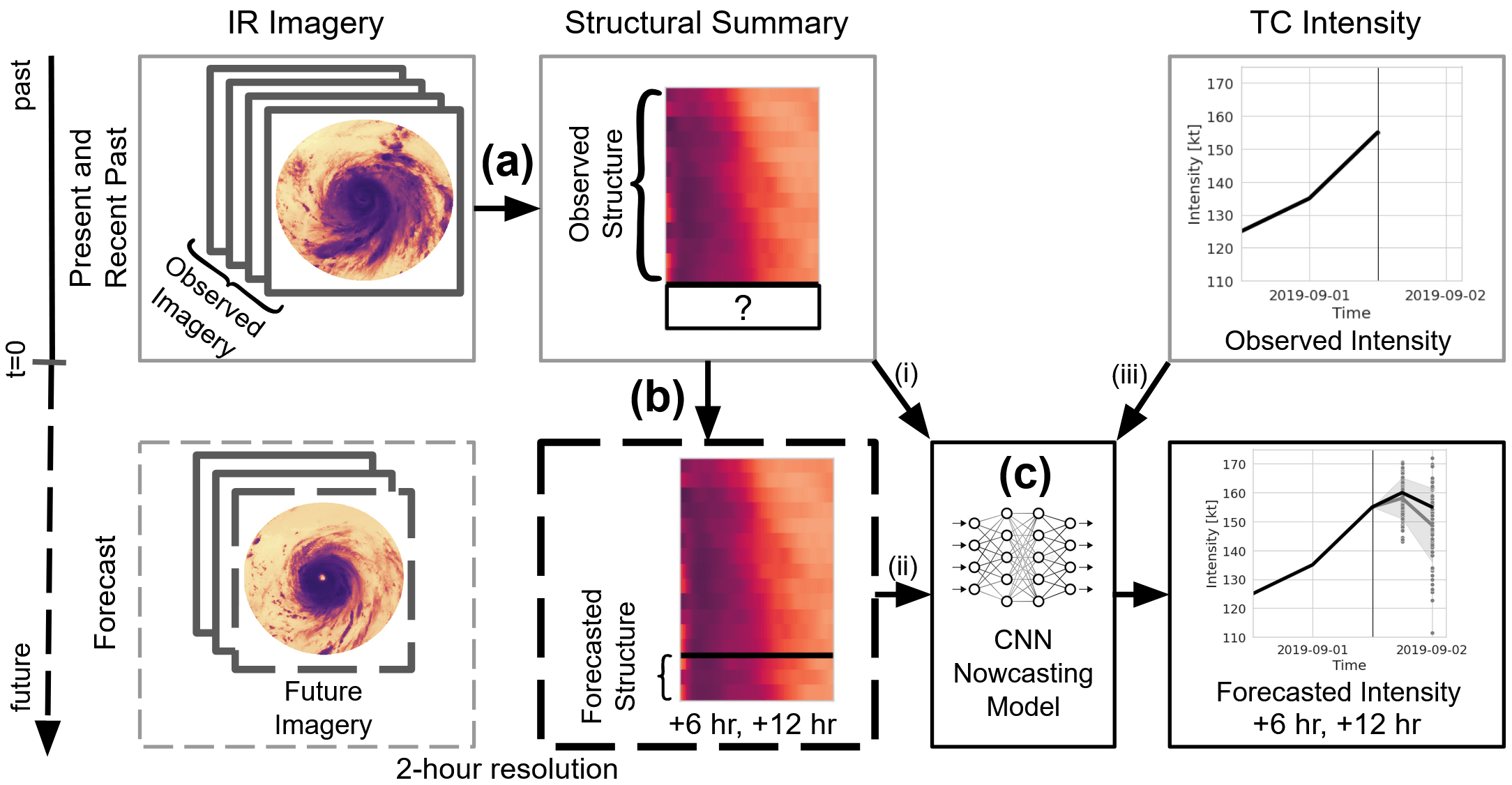
Structural Forecasting for Short-Term Tropical Cyclone Intensity Guidance
This work presents a new method of short-term probabilistic forecasting for tropical cyclone (TC) convective structure and intensity using infrared geostationary satellite observations. Our prototype model’s performance indicates that there is some value in observed and simulated future cloud-top temperature radial profiles for short-term intensity forecasting. The non-linear nature of machine learning tools can pose an interpretation challenge, but structural forecasts produced by our prototype generative model can be directly evaluated and may offer helpful guidance to forecasters regarding short-term TC evolution.
Weather and Forecasting, 38(6):985-998, 2023