
Theoretical and Computational Biological Physics
Part of the Biological Physics Initiative
Carnegie Mellon University, Department of Physics
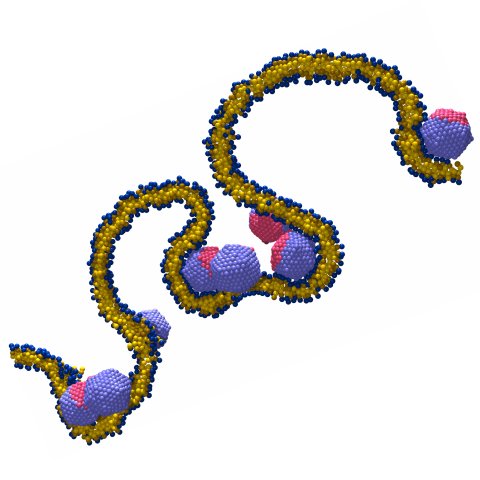
The rigatoni approach to bilayer elasticity
Vagelis A. Harmandaris and Markus Deserno; J. Chem. Phys. 125, 204905 (2006).
The tensile force along a cylindrical lipid bilayer tube is proportional to the membrane's bending modulus and inversely proportional to the tube radius. This relation, which is experimentally exploited to measure bending rigidities, can be applied with even greater ease in computer simulations. Using a coarse-grained bilayer model we have shown how one may efficiently obtain bending rigidities that compare very well with complementary measurements based on an analysis of thermal undulation modes. One particularly remarkable finding of this investigation was that no deviations from simple quadratic continuum theory occur up to a radius of curvature comparable to the bilayer thickness.
Bending rigidities have been measured experimentally by various techniques all ultimately based on one of two general approaches: One may either utilize the dependence of thermal undulations on a membrane's rigidity, or measure the force needed to actively bend it. The traditional realization of the first approach is to monitor the fluctuations of vesicles as a function of wavelength by light microscopy, a method termed "flicker spectroscopy". A related experimental method is based on micro-pipette manipulation techniques. There, the flicker spectrum is successively suppressed by increasing the pipette pressure, and the bending rigidity can then be obtained from the low-tension regime of the tension-area curve. The second approach is typically implemented by measuring the force needed to pull nanoscale bilayer tubes (tethers) from vesicles. Since the formation of a tube involves the creation of a high curvature, the work to pull a tether is basically done against bending energy, hence the modulus can be determined from it.
Determination of the bending rigidity is of course equally important in computer simulation studies of lipid bilayers, and the spectrum of available methods is the same. However, by far the most common approach in simulations is flicker spectroscopy, both for atomistic simulations as well as for various coarse grained methods.
Basically, one simulates a nearly flat membrane, spanned across the xy periodic boundary conditions of the simulation box, and monitors its fluctuations in a wave vector dependent way. Within linearized Helfrich theory it is easy to see that the mean-squared amplitude of a membrane Fourier mode is given by
![]()
From this spectrum the bending modulus kappa can be extracted by suitable fitting.
Despite being so common, this method has two important disadvantages. First, Large values of the bending modulus lead to very small amplitudes, which meakes it difficult to resolve the flicker spectrum. Second, the curvatures which are actually probed are very weak. It is not too difficult to see that in the tensionless state the mean radius of curvature which is excited by thermal fluctuations is several times the system size. In fact, using the fluctuation spectrum calculated above, we easily see:
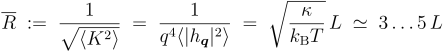
This is evidently much bigger than what one would really like to do to a membrane under many circumstances. This leaves the question open how relevant the measured elastic constants really are.
We proposed the following alternative method: Create a cylindrical vesicle, spread over the periodic boundary conditions of the box, as illustrated in Figure 1 on the right. Both frames a) and b) have the same number of lipids, but a) has a shorter box and therefore a larger tube radius. This also means that the bending energy in a) is smaller, and this means that generally cylindrical vesicles exhibit a tensile force along their axis, because they try to shorten their length in order to increase their radius. Since the ultimate reason for this force is bending energy, it should be possible to obtain the bending modulus from this force, and indeed it is easy to show that the following very simple relation holds:
![]()
In other words, we only need to measure two things: the axial force F along the tube direction and the radius R of the tube. It is the latter quantity which prevents this simple method from being directly applied in experiments. While it is comparatively easy to measure forces in the piconewton range (by means of optical tweezers), the vesicle radii typically turn out to be suboptical, hence there is no direct way of obtaining R and exploiting the above simple formula. More tricky things need to be done.
We have performed such a measurement for a coarse-grained lipid bilayer model with a series of vesicles, all with the same material properties, but with different vesicle radii. The result is shown in Figure 2 on the right. As can be seen, the force does indeed decay inversely proportional to tether radius. The inset shows the product of force times radius (divided by two pi) as a function of cylinder curvature, expressed as the ratio of bilayer thickness w and vesicle radius R. Remarkably, the resulting value is constant within the error bars (in our case about 12 kT), even though the radii of curvature evidently approach bilayer thickness! Hence, simple quadratic curvature elasticity seems to be a perfectly correct description of our membrane model up to extremely high curvatures.

Membrane bending rigidities are traditionally determined from their fluctuation spectrum. However, actively bending them might not only be a faster approach to the problem, it can give crucial information about the strong bending behavior.
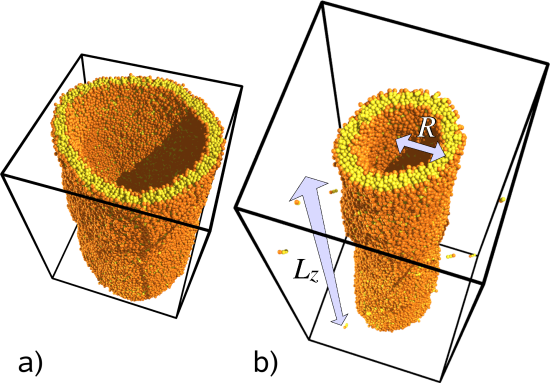
Figure 1: Simulation of cylindrical lipid membranes spanned across the periodic boundary conditions of a simulation box. Both tubes have the same number of lipids, but the second one has a smaller radius and hence a higher curvature energy. As a result, it is under a larger tensile force F.
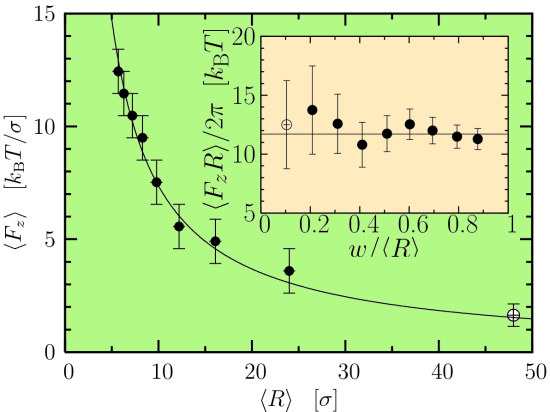
Figure 2: Force F as a function of tether radius R, and the product FR as a function of R (inset). The latter is proportional to the bending rigidity κ and essentially independent of R, even for very small R, showing that even for very large curvatures the simple lowest order elastic theory works very well.

Looking for a postdoc, PhD position or under-graduate research project or similar? Have a look at our announcements!

Funding:


![]()