Research Projects
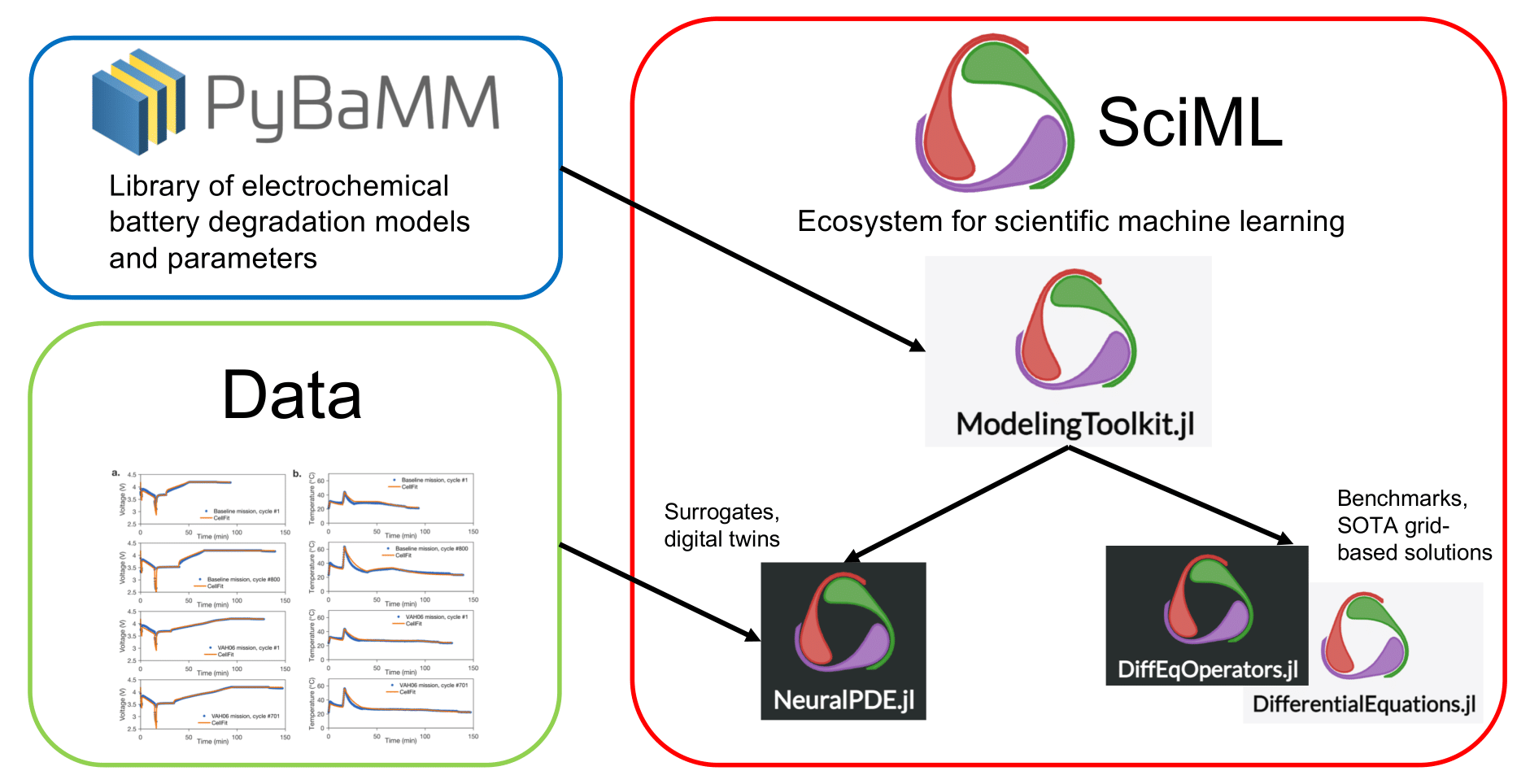
Cell-scale battery modeling (P2D/DFN models)
We are generating cell-scale battery models from porous-electrode theory (such as the P2D/DFN model) from PyBaMM in ModelingToolkit.jl to leverage the simulating power of the SciML ecosystem - either using Method of Lines (finite differences then ODE/DAE solvers) or by surrogatization with Physics-Informed Neural Networks. We will also develop hybrid models that directly incorporate experimental data into the models.
Integrated workflow for automated around-the-clock experiments
We integrated each section of the workflow to build an automated data pipleine which enables experiments to run 24 hours a day. Modeling results are saved to the database and used in the next sequential learning cycle.
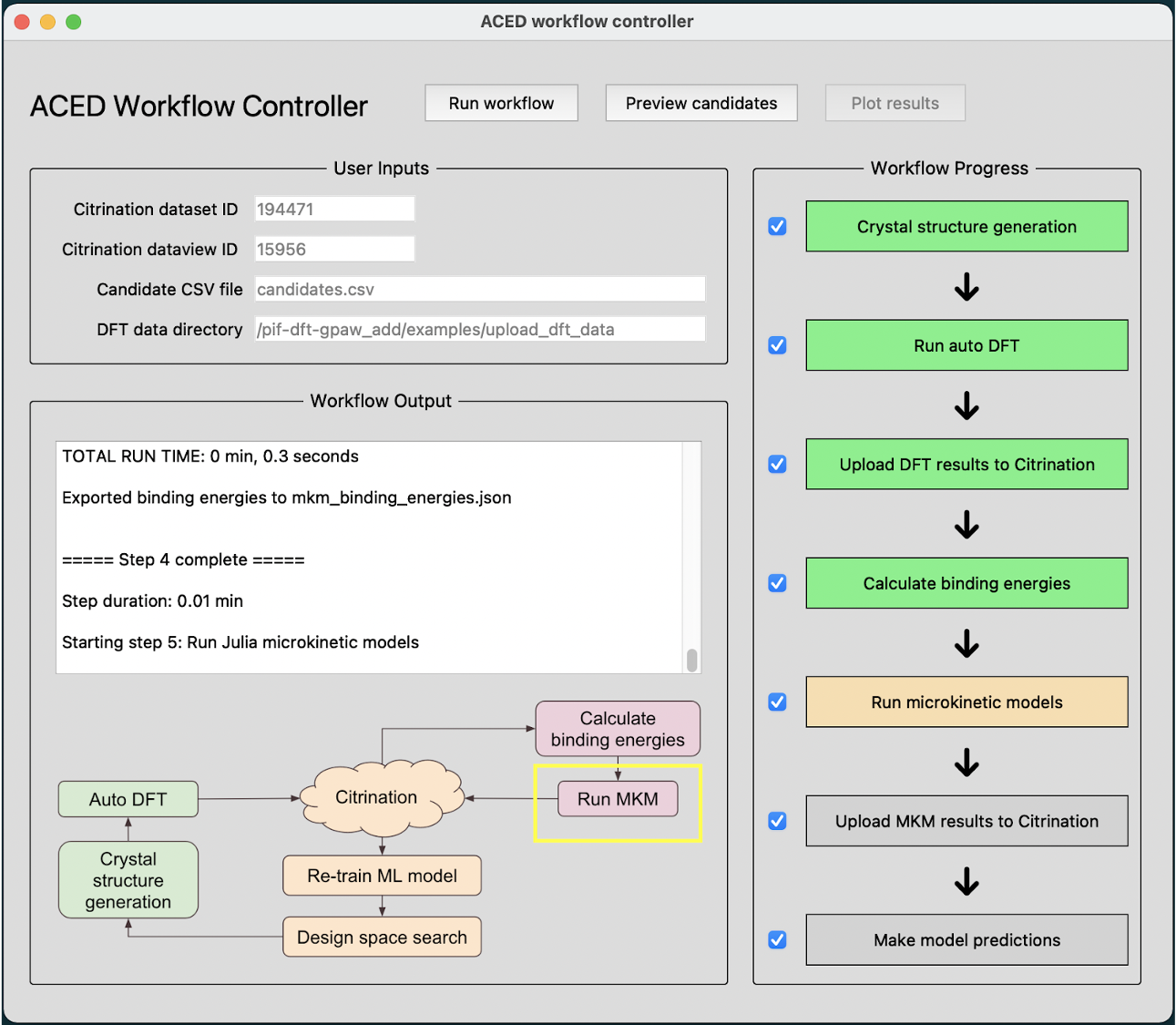
High-throughput density functional theory calculations
To rapidly generate a large-scale database of reaction intermediate structures, we are developing an automated DFT framework. This will simultaneously accelerate adsorption energy computations while systematically accumulating and manipulating output data in a manner for ease of integration into machine learning models. Moreover, it will facilitate the overall closed-loop sequential learning approach to explore new systems.
Sequential learning for design of experiments
We will perform physics-aware machine learning to iteratively guide simulations towards candidate materials. This sequential learning approach will enable an efficient and uncertainty-driven exploration of the high-dimensional design spaces encompassed in this work while allowing for multi-objective optimization of catalyst parameters.
Physics-informed Surrogate ML Models
Building on the success of methods such as Crystal Graph Convolutional Neural Networks and Equivariant Neural Networks in predicting properties of crystalline solids as well as software packages for molecular machine learning such as DeepChem, we are developing software to combine these techniques to rapidly and accurately predict energetics of the adsorption processes critical to catalysis of reactions such as nitrogen reduction, as well as to screen novel electrolyte molecules and blends.
Accelerated solution of microkinetic differential equations
Leveraging the advanced numerical techniques implemented in the Julia programming language, we are developing customized solutions to dramatically speed up the solutions of the challenging stiff differential algebraic equations (DAE’s) that describe the interactions of chemical species on catalytic surfaces.
