
Theoretical and Computational Biological Physics
Part of the Biological Physics Initiative
Carnegie Mellon University, Department of Physics
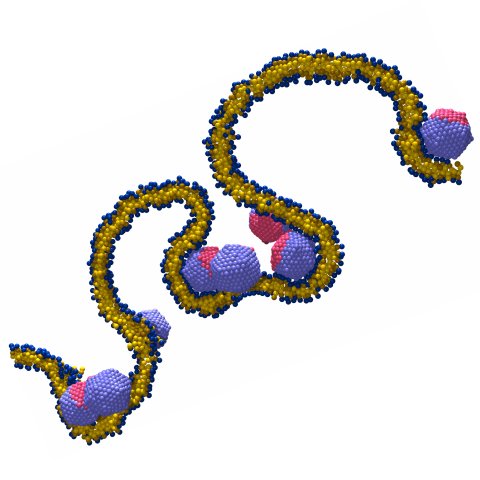
Genome packaging inside viruses — with a twist
Igor M. Kulic, Denis Andrienko, and Markus Deserno; Europhys. Lett. 67, 418–424 (2004).
Single polymers collapse from a random coil conformation to a dense state once the solvent gets sufficiently poor. For a flexible chain the condition of minimal surface energy yields an approximately spherical globule, but for semiflexible polymers the situation is more complex: The local structure of the dense phase then consists of essentially straight chains with a basically parallel alignment, in order to minimize bending energy and maximize density, respectively. Such a state can be characterized by a smooth field of tangent vectors, but in the spherical case this field must have at least two energetically unfavorable defects on the surface (you can't comb a sphere). However, for a torus many defect-free fields are possible. Indeed, DNA, the probably best studied semiflexible polymer, readily forms beautiful nanotori after adding any one of a variety of possible condensing agents (like polyethylenglycol (PEG), multivalent counterions, or bundling proteins) to a dilute solution of DNA chains. These tori are surprisingly monodisperse, having a radius comparable to the persistence length of DNA (about 50 nm) basically independent of the condensation method.
However, if one thinks of these toroids as simple circumferentially wound "spools", one realizes that the DNA strands on the inner side are rather strongly bent, while the ones on the outer side bend much weaker. In other words, bending energy is quite unevenly distributed. Since the bending energy e per unit length is inversely proportional to the local radius of curvature r, i.e. we have e~1/r2, a simple version of Jensen's inequality, <1/r2> > 1/<r2> will convince us that the system can lower its bending energy by redistributing curvature.
The question now is: How should the system do this? We propose that a viable mechanism for evening out the curvature distribution is to twist the bundle of DNA strands while circumferentially winding. This then would suggest toroidal aggregates whose structure is illustrated in Fig. 1 on the right. How can one describe such a complicated state quantitatively? And in what sense can one argue that it has a lower energy? In order to address this question we first restricted our description to the field of tangent vectors to the DNA condensate. This simplifies the situation for two reasons: First, it removes problems related to the connectivity of the chain, and second, it basically immediately tells us that the appropriate energy functional to look at is the Frank-Oseen energy of a liquid crystal. This energy functional contains three contributions corresponding to the three possible elastic deformations of a nematic liquid crystal: splay, twist, and bend. We must set the splay deformation to zero, because we want a divergence free vector field (which will preserve the density of DNA strands), but the other two elastic constants are generally nonzero. The bend-deformation turns out to correspond exactly to the usual energy of bending a semiflexible rod, but the twist deformation is something new: It penalizes the twisting of a bundle of DNA strands, and its elastic constant is typically lower than the bend-constant.
We now find the following scenario: If the torus has a big hole ("slim torus"), bending energy is already reasonably evenly distributed. Any attempt to further lower the bending energy would simply cost too much twist energy. However, for a torus with a very small hole ("fat torus") the energy gain upon redistributing curvature energy is so large that it pays off even though it has to pay a twist energy prize. In fact, as a function of the ratio of the two torus radii one finds a clear continuous phase transition between an untwisted and a twisted state. One can even plot a structural phase diagram which contains as its two axes the ratio between torus radii (horizontal) and the ratio between twist- and bend-moduli (vertical). In this diagram, which can be seen in Fig. 2 on the right, one finds a clear boundary between untwisted states and twisted ones. This boundary can be found either by a full numerical minimization of the Frank-Oseen functional (heavy dots), or alternatively by a suitable variational ansatz (bold solid line; the dashed line is an improved ansatz).
WInding up an elastic cable onto a toroidal spool costs a lot of energy for the parts close to the inner hole. This large penalty can be reduced by inducing an overall twist of the wound-up bundle, even if twist itself also costs energy.

Figure 1: Illustration of the winding pattern of a toroidal spool that has reduced its bending energy by assuming a twist.
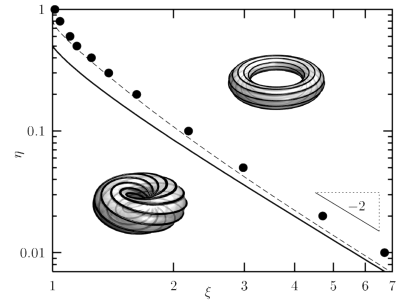
Figure 2: Phase diagram for the twist bend instability. The boundary between an untwisted and twisted winding pattern can be found either by a full numerical minimization of the Frank-Oseen functional (heavy dots), or alternatively by a suitable variational ansatz (bold solid line; the dashed line is an improved ansatz).

Looking for a postdoc, PhD position or under-graduate research project or similar? Have a look at our announcements!

Funding:


![]()