JoSS Article: Volume 7
The Art and Science of Dynamic Network Visualization
Skye Bender-deMoll, skyebend@stanford.edu
Nehalem, Oregon
Daniel A. McFarland, mcfarland@stanford.edu 1
Stanford University
Abstract: If graph drawing is to become a methodological tool instead of an illustrative art, many concerns need to be overcome. We discuss the problems of social network visualization, and particularly, problems of dynamic network visualization. We consider issues that arise from the aggregation of continuous-time relational data ("streaming" interactions) into a series of networks. We describe our experience developing SoNIA (Social Network Image Animator, http://sonia.stanford.edu) as a prototype platform for testing and comparing layouts and techniques, and as a tool for browsing attribute-rich network data and for animating network dynamics over time. We also discuss strengths and weakness of existing layout algorithms and suggest ways to adapt them to sequential layout tasks. As such, we propose a framework for visualizing social networks and their dynamics, and we present a tool that enables debate and reflection on the quality of visualizations used in empirical research.
I. Introduction
For the most part, the social network community employs relatively static notions of networks. Even though classic studies of network change have collected data on networks over a period of time (see Doreian and Stokman 1997 for a review), the data are collected in discrete waves, and the intervals between the waves of these surveys are quite long. As such, the history of each relationship is partial at best and leads scholars to infer micro-dynamics of network evolution without ever observing them directly. But this is beginning to change. Innovations in data collection (Choudhury and Pentland 2004; Choudhury 2004; Motoyoshi et al. 2002), the application of network methodologies to new fields (Barabasi 2002; Dunne et al. 2002; Powell et al. 2005), and the use of simulations as data sources (Ashish et al. 1995; Banks and Carley 1996; Carley 1999; Jin et al. 2001) are yielding data with high sampling rates, and occasionally time data that identifies when changes arise in individual relations (Roy 1983; Morgan et al. 1995; Rothenberg et al. 1998; Gibson 2003; McFarland and Bender-deMoll 2003). This wealth of data presents new opportunities for theorists (Moody et al. 2005), requires refinement of statistical and modeling techniques (Wasserman and Pattison 1996; Snijders 1996; Snijders and Van Duijn 1997; Robbins et al. 1999; Snijders 2001), and gives us occasion to question assumptions of the relationship between interaction and network social structure. It also presents a new set of challenges for conceptualizing, visualizing, and communicating information about social networks. If scholars hope to tease apart the relations between network phenomena at various timescales and levels of aggregation, then we will need tools to help us explore the parameters and their implications.
Recently, considerable attention has been paid to the realm of graph or network visualization, with research taking place in multiple fields (McGrath et al. 1997; Freeman et al. 1997; Krempel 1999; Freeman 1999, 2000a, 2000b; Brandes et al. 2001; Johnson 2002; Luckovich and Johnson 2004; Krempel and Plumper 2004; Batagelj 2004; McGrath and Blythe 2004). This research has several threads: visualization of compiler graphs or code structure, visualization of acyclic trees (Di Battista et al. 2000), very large datasets (Munzner 1997), as well as the more moderately sized social networks (Freeman 2000). These domains are distinguished somewhat by the approaches and techniques necessitated or facilitated by the data. Obviously there are many more domains, and reviews of them exist elsewhere (Freeman 1999; Himsolt 1995). We are mostly concerned here with visualizing social network data sets that change over time. These networks tend to be small to medium sized networks (<1,000 nodes), with directional ties that are fairly sparse, and which often entail cycles (unlike trees), bridging connections, isolates, and disconnected components. Moreover, these networks generally lack an a priori criterion for ordering or placing structures in a privileged relationship on a layout (Krempel 1999; Krempel and Plumper 2004). Unlike circuit board layouts or orthogonal-graph drawing, we are mostly interested in "straight line" layouts that place less emphasis on the actual routing of the ties between nodes, except for considerations of aesthetic or visual accessibility.
For the most part, algorithmic work on network layouts has been devoted to static graphs. Much of it is based on the concept of "force-directed" layouts (Kamada and Kawai 1989; Fruchterman and Reingold 1991; Frick et al. 1994), or the projection to lower dimensionality with various techniques (Harel and Koren 2002; Kruskal and Wish 1978), or the direct optimization of layout criteria (Davidson and Harel 1996). Within these general classes there are various models and means of optimization (e.g., simulated annealing, steepest decent, matrix projections, etc.) with, as we will argue later, quite a bit of overlap between them. There are several software packages that implement these algorithms. Some of the most widely used are Pajek (Batagelj 1998, 2004), GraphVis (AT&T Labs 2003), NetDraw (Borgatti 2002), and others (Krackhardt et al. 1994; Himsolt 1995). They have done much to expand the realm of possible visualizations, allowing three-dimensional layouts, stepping through networks in time, use of colors and shapes to communicate categorical variables, layouts of large graphs, integration with descriptive statistics, and multiple import and export formats.
As useful as these programs are, they have received some valid criticism. If graph drawing is to become a methodological tool instead of an illustrative toy, various concerns need to be overcome. First, a basic issue with many of the network visualization programs is that even though they rely on published algorithms, the exact details of the implementation are obscured in the compiled code.2 This matters because many of the algorithms rely on simulated annealing or other optimization processes in which the results can be highly dependent on the parameter settings and stopping criteria. It can be difficult for the user to tell if a layout produced is an optimal one, or simply the result after a set number of iterations. In addition, the necessary steps for modifying and transforming the network data to produce a layout are seldom fully expressed in documentation. The exact implementations of the algorithms and their parameter settings vary across software packages and are rarely made explicit, so it is difficult for researchers to reproduce and critique each other's published work and to engage in scientific debates that advance the accuracy of empirical research.
Second, there are few well-defined criteria for assessing how "good" a graph layout is. There are many possible ways to position the nodes and arcs of a network, some of these layouts convey certain relationships more accurately or emphasize different features. As with any chart or figure, it is possible to intentionally or accidentally obscure information so as to mislead the viewer about the information in a graph. Perhaps because graph visualizations tend to be compelling and relatively new, most people do not know what criteria to use in assessing a layout's informational validity, and tend to either accept them at face value or dismiss them completely. Some algorithms do include criteria for evaluating the layout on specific undesirable features (line crossings, bends, obscured nodes, etc.; see Davidson and Harel 1996 and Di Batista et al. 2000 for some distributions) but a system ranking the actual geometric arrangement of the nodes has been elusive.
The geometrical layout of a graph is not the only feature that needs careful consideration. A useful technique for conveying information about the relations in a network is to use graphical attributes of the nodes or ties (color, width, dashing, etc) to symbolize attributes of the relation. In situations where multiplex ties are possible, it becomes difficult to use this as an accurate graphical indicator because ties may obscure each other. High graph density or overzealous iconography can result in layout clutter. If researchers are going to make claims from their visualizations (for example, that there has been a compositional shift in the network between two time points because there has been a shift in the prevalent color of the layout), it is crucial to be sure that graphical changes are directly related to the balance of attributes and not simply determined by the order in which the program draws elements to the screen.
In our design of the SoNIA package, we attempt to address these criticisms—more successfully with some than with others. But our main consideration in extending previous work is to handle network data and visualization in ways that explicitly deal with its time-based nature and aids understanding what the data really mean. However, work on the project has followed the needs of its developers, so it is fairly uneven in completeness of implementation and testing, and leaves some interesting possibilities unexplored. SoNIA is currently a working prototype (or proof-of-concept model) that demonstrates some possibilities for depicting time in network layouts.
II. Complicating Networks: Rate and Time
The majority of networks that social network analysts describe are considerably more abstract than the physical networks of power-grids or wired computer networks. They often consist of elicitations of an individual or a group's mental construct of surrounding social structure, such as that consisting of friends, enemies, advice-givers, etc. Related to but somewhat distinct from these "cognitive networks" (or abstracted relations; see Marsden 1990) are networks based on a recorded series of events—e.g., emails, weblinks, loans, citations, sexual contact, conversations—which, when taken in aggregate yield “behavioral networks” for analysis.3 In some cases the network data itself is the focus or phenomena of interest. In other cases the network data are only considered to be a proxy or quantifiable aspect of the "real" network of interest, which may actually be better described by some complex function of a collection of variables. As such, surveyed degrees of "liking" or "disliking" can be viewed as a means of eliciting a "friendship network" (Newcomb 1961), and marriage records may be regarded as an indicator for a "family alliance network" (Padgett and Ansell 1993).
The point of making this distinction between abstract networks of interest and actual event data is that the pace of dynamics in the abstract network may be very different than the pace of event data. For example, a friendship network can be considered an abstraction from the actual set of people's individual positive and negative interactions. The degree of warmth Ann feels and expresses towards Betty may fluctuate over a single day, or even a class period but, from the perspective of another party, their "friendship" is an ongoing relation that grows over a period of days. The need for this distinction and the necessity of explicitly considering data aggregation is somewhat obscured when the timescale of data collection is equal to or greater than that of the network of interest. Fluctuations in the observed variables can take place at a rate much faster than the sampling period. In fact, such fluctuations may be considered "noise" in the measurement of the observed network, and much of it can be suppressed by carefully structuring the survey instrument.
For example, imagine a daily network survey that asks questions about how respondents are feeling about each other at the moment they take the survey. The response Ann gives could be strongly influenced by a temporary disagreement with Betty. If these values in daily surveys were averaged each week as friendship strength, then the fluctuations might wash out, and suggest a moderately deep friendship.4 If the survey were only performed weekly, the effect of an isolated negative remark would likely be missed, or it would be considered an outlier or an error unrepresentative of their generally good relations. An alternate methodology might ask respondents to rate their friendships over the past week, in a sense asking them to perform a kind of averaging or aggregation: Although Ann might be hurt by Betty's remark, she knows Betty has been a good friend, and still rates their friendship highly. In fact, this kind of "averaging by the respondent" is quite common in social network analysis work, partially due to people's demonstrated tendency to give "average" responses to questions about a specific period of time (Marsden 1990; Killworth and Benard 1976, 1979). Although this feature of using the respondents to filter the "raw" data to yield an "abstract" network of interest may be a convenient aspect of many social network studies, such limits on temporal resolution may impair our ability to investigate important aspects of dynamic networks.
This issue, that the fast dynamics or "noise" in one level of analysis is the phenomena of interest in another, is a challenge for other areas of science as well, particularly in thermodynamics and complex systems. In describing physicists' approach to measurement of quantities that appear fixed in one time frame but fluid in a longer view, Bar-Yam proposes a separation of time scales:
The separation of timescales assumes that our observations of systems have a limited time resolution and are performed over a limited time. The processes that occur in a material are then separated into fast processes that are much faster than the resolution of our observation, slow processes that occur on a longer timescale than the duration of the observation, and dynamic processes that occur on the timescale of our observation. (Bar-Yam 1997: 90)
This emphasizes the importance of considering how the sampling rate of data collection relates to the timescale of the phenomena of interest. Although it may be possible to use medium-paced measures of change in a network in combination with a well-developed theoretical model of the underlying processes to achieve a statistical estimation of the fast-paced dynamics that may have occurred (Snijders 2001), this should not be confused with collecting fast-paced data. If there are only three waves of data, perhaps we can talk usefully about network change, but it is difficult to argue that "dynamics" and “evolution” have been recorded.
The reality of social network measurement is that there are obvious practical limitations to the time resolution that can be achieved with survey instruments. There are stubborn methodological issues such as memory effects of respondents, test-retest reliability, etc. (Ferligoj and Hlebec 1999). However, some of these problems are less prevalent for observation-based data, computer data, and other automated data collection techniques. As advances in technology and methodology increase our ability to collect larger and larger volumes of raw data with accurate information about the timing of events, it is still crucial that we explicitly consider how the raw event data relates to the abstract network we want to analyze or visualize. We cannot expect visualization techniques to give stable, consistent, useful results unless the definition of the social space we are trying to visualize is itself stable and consistent. This means that when working to draw a network, we should have a clear sense of the functional relationship between the data and the underlying "network" that we want to picture. Pinning this down, however crudely, will help decide what transformations and aggregations need to be applied to the raw data.
There are several ways of rendering event data into networks of relations. Frequently, the distinction between time scales is not really made, and whatever data are available are analyzed at the level most convenient to collect and analyze. Usually this requires some form of temporal grouping as the data are not collected instantly, or they may deal with events taking place over a period of time. The most straightforward aggregation technique is simply to lump all the available data into a single network. If there are three emails between Bob and his boss, we will just give them a tie with strength equal to three. But is using the count of ties the best way to represent the network? Should emails be weighted by the amount of text in them? Perhaps there are enough data points and time information to use the rate of communication instead of the volume? Should we parse time into days and then use the average number of emails per day? Or should we use weeks?
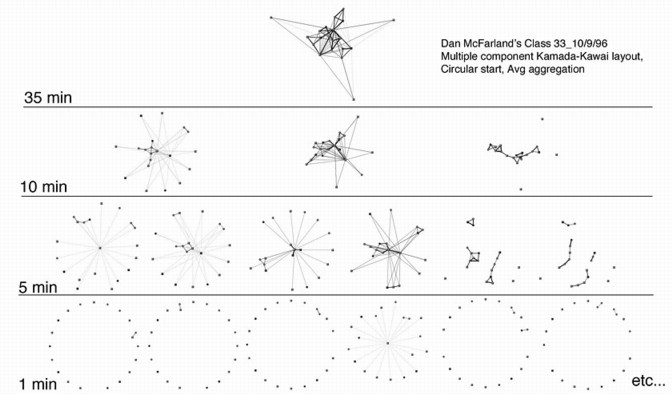
We use the term aggregation to describe the process of grouping event data about relationships (e.g., individual ties, ego networks, or complete sets) from a bounded range of time into a single network. While aggregating all of the collected data may give a network with the greatest range and detail, it means disregarding all of the time information and ordering of events. Aggregation creates interesting problems where events are considered simultaneous (and therefore statistically independent to some degree) when in fact they may be ordered and directly dependent. Consider a continuum (see 1 above), with a static network (complete, rich, detailed, but unchanging) at one end and individual events (sequential, dyads or triads, rapid, causal, ahistorical) at the other (Collins 1981).
Data at the "event" level of time-aggregation does not fit the standard notion of "a network" well, yet it is at this micro-level of action where simulations of network processes will need to function. To tease apart the relations between these lower level building blocks and higher order patterns, we need to consider how we measure time and record events. Are the higher-level patterns nothing more than the sum of the events? How much time is "enough" to be able to describe change in a network? At what levels are dyad-level (asymmetry, reciprocity, exchange) and triad-level (balance) effects visible? At what time-scale do network-level (activities, cliquing) effects appear?
III. Discrete vs. Continuous Sampling and Discrete vs. Continuous Time
When analyzing or simulating a process, it is important to consider the distinction between discrete and continuous variables. Most processes in the real world are assumed to be continuous, meaning that the descriptive parameters vary relatively smoothly through a series of values at changing rates. Continuous systems are so named because they are usually described mathematically by differential equations that give (for the most part) continuous results at whatever point they are evaluated. To actually collect data on these systems or to model them on the computer paradoxically requires sampling them at a series of regular discrete points in time. This yields data points described by real-valued numbers (decimal or floating-point) that are non-continuous but which reasonably approximate the continuously changing process. The accuracy is determined by how frequently the samples are made, and to how many decimal places they are measured.5 There are also some phenomena that appear discontinuous and are well described as a sequence of transitions between discrete states. These discrete processes are generally modeled with “difference” rather than “differential” equations. Discrete data only take on values from a certain set (integers corresponding to states, for example). If we were talking about networks, continuous values might be used to describe tie weightings such as probability of interaction or volume of trade, where discrete valued ties could either be dichotomous (0 or 1, present / absent) or a set number of categories (friend, acquaintance, unknown). As we have already implied, it is, of course, possible to transform or translate data from one framework to the other. We can try to fit a continuous function to discrete data-points, or resample a continuous function. We can also aggregate discrete events and calculate a continuous function that gives the rate at which discrete events are occurring.
This distinction between the two ways of measuring things comes into play at several levels when we consider networks. First, the "actual" underlying network process may be classified as discrete or continuous, depending on the theoretical framework the researchers are using. Second, either strategy can be used for collecting and coding the data. Either strategy chosen for collecting or sampling the data implies a particular discrete or continuous model of time. This is what we are concerned with in this paper: considering the particularities of handling time implied by each approach.
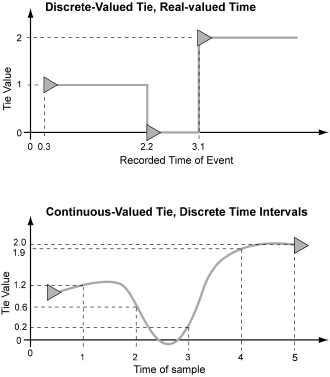
Consider a network as a collection of variables, each describing one relation, each varying smoothly in time. We might describe the variables with a large number of difference or differential equations, presumably coupled in some complicated way (unless dyads are independent). With this approach we could, in theory, know the exact state of the network at any chosen moment, but the resolution in measurements necessary to create this kind of exact model is rarely available in real experimental data. Usually such a continuous process can only be approximated using a discrete time methodology, i.e., sampling the network variables at regular intervals and recording the value of each tie at every sample point. This gives us a large bundle of parallel time series, one for each relation. Or instead of thinking of it in series, we can arrange all the data for each sample in a matrix that describes the point in time. This is the matrix approach is implied by most multi-wave network surveys. But the series of matrices, each of which is a snapshot of the whole network at one point in time, is really a discrete sampling of a set of ties that are changing continuously.
The problem with any sampling technique is that some data is always missed, especially if there are only a few sample points. What happens between the survey points? Smooth variation? Sudden shifts? Changes that cancel out? With this approach, fluctuations in the network can only be detected if they take place on a time scale larger than the sampling rate. For network data, this can be a problem as even the best network data generally has less than ten time points. If parameter estimates for a dynamic network model are based on under-sampled data, they will be inaccurate (Leenders 1997). But (hypothetically anyway) the sampling rate can be increased to capture the dynamics. In other words, if the network is continuous, a good strategy is to measure it in discrete time but to carefully consider the sampling, using the highest feasible rate.
Another approach is possible if the network is discrete and ties change directly from one state to another. Each change can be viewed as an event rather than a gradual transition. If all tie changes occur simultaneously, then we could use the discrete time approach and sample the network after each set of changes—perfectly capturing the discrete dynamics of the network. However, in most real systems, the changes may occur independently for each tie at any time, and the discrete approach might miss some changes. A continuous time methodology, therefore, would record the real-valued time coordinate for each state-change or event when it occurs. The entire network is not observed at once. Rather, a "stream" of (usually asynchronous) tie value changes is recorded along with the time coordinate of the transitions. This kind of streaming data does not directly yield a "network" or normal matrix, but it does preserve the order and sequence of events in precise detail, making it possible to output networks later by using various binning techniques.
The contrast between the different approaches becomes apparent if we try to assign time coordinates to the data. The discrete approach breaks time down into a series of chunks or blocks within which all finer graduations are irrelevant. This is often useful because it simplifies description and recording, and events within a block are assumed to occur simultaneously without influencing each other. When numbers are used discretely, they refer to a chunk of time rather than to a point in time. For example, 1 refers to the 1st chunk, 2 to the 2nd, etc. This is very straight forward, but can be confusing when we want to describe an interval.6 Does "1 to 2" mean "1 and 2"? Does "from 1996 to 1997” mean “all of 1996 and 1997” (two years), or just “from the beginning of 1996 to the beginning 1997” (one year)? If we are using discrete intervals, "1 to 2" means two units of time, where in the continuous approach, "1 to 2" could mean either "1.0 to 2.0" (one unit of time) or "1.0 to 2.99" (very close to two units of time). It is possible (and necessary) to work with both kinds of time, but in order to combine them in ways which allow for a meaningful visualization, it is crucial to be clear about which mode is used by various kinds of data and how they relate to the underlying network.
IV. SoNIA'S Concept of Time, Events, and Networks
The SoNIA (Social Network Image Animator) package is not intended to be a network analysis tool. Rather than focusing on calculating network properties and indices, it is designed to facilitate the exploration of dynamic relational data, and the comparison of various layout techniques for making reliable animations of networks. Because of this, we have employed what we hope is an extremely flexible and extensible notion of a "network," and have attempted to implement the underlying data structures to support this.
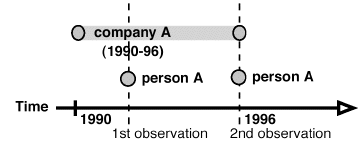
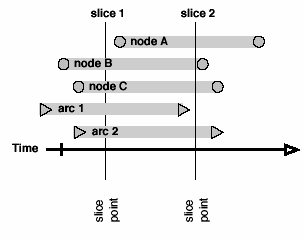
In the conceptual framework we use for SoNIA, networks are not limited to the standard notion of a set of relations among a set of entities at a given point in time. Instead, consider the entities (or nodes and individuals) as a stream of events. Every event has a real-valued time coordinate indicating when it occurs. If the event is not instantaneous, it also has an ending coordinate to indicate its duration. A node-event, for example, can describe a company that comes into existence on January 1, 1990, and then dissolves on June 1, 1996. Alternatively, a node event might describe a single observation of a node, such as an individual in a friendship survey administered in 1995. This case might be considered an "instantaneous event" in which the existence of an individual in the dataset was determined in a single snapshot. The individual might still be in the data at a later snapshot, but this would be treated as a second event with the starting time of the data collection and with no duration. This can be illustrated using a "phase diagram" in which horizontal bars indicate an event ongoing between observation points, and circles indicate instantaneous observations (figure 3).
Node-events can describe more than just the presence of a node in the data. They can also indicate changes in the node's attributes (or in our case, the iconic representation of the attributes: color, shape, size, labeling, etc). In a sense, an event can be thought of as piece of information (existence, an attribute, sometimes coordinates) describing an entity (the node) at a position in time. Arc-events function in much the same way, except that they are tied to two entities, the sending and receiving nodes. In this framework multiple ties, multiplex ties, or ties overlapping in time are completely permitted.7
There are several advantages to this structure. One is efficient storage and computation because it is essentially a list-based approach, which helps for storing large, sparse networks. It also provides some conceptual clarity for expressing nodes' changing attributes, and changing network sizes. But the main advantage is that data can be easily transformed into more traditional matrices or arc-lists for calculations or visualization in a way that is both flexible and encourages careful consideration of the theoretical structure backing the data and its time mode (i.e., discrete vs. continuous).8 We refer to this process of acquiring networks from the set of event data as "slicing." Slicing is a metaphor that helps describe a network at a specific point in time as a cut through the trajectories traced out by each entity in the state-space.
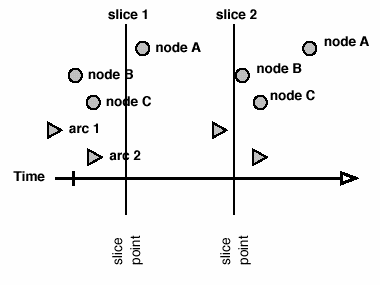
To generate a slice network, the set of node- and arc-events is queried to return all events that fall in the time range of the slice. Consider two kinds of slices that can be made. Instantaneous or "thin" slices occur when the slice has no duration, the start and end times of the slice are the same, so the slice only contains events with exactly the same time coordinate, or events with durations intersected by the slice (see figures 4a-b).
The thin slice may be more appropriate when network data is collected with explicit duration information. Thin slices give the response to the question "show me the network at time t.” But if the network data is instantaneous instead of duration-based, each event describes only a single point on the timeline, so it is quite likely that the time slice at t will fail to intersect any events, and an empty network would be returned. In this case, using a thick slice (a discrete chunk of time) would be more appropriate.
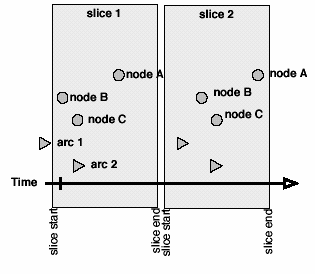
Thick slices have start and end times that define an interval, and include all events that either occur within the interval or whose duration intersect the interval (see figure 4c).9 Thick slices query the data similar to the way a questionnaire might ask about ongoing or past relationships. For example, "show me all the loans among firms that took place during 1994.” It is not a picture of a network at a point in time but rather a period in time, a collection of data within a certain range, as in the bin of a histogram. Thick slices are a way of discretizing (pseudo-) continuous data, and thin slices are a way to sample continuous or real-valued versions of discrete-interval data.
A slice is a “bin” that contains a set of events in time, but for most network operations, the time information is not used and the network data must be collapsed to form a matrix or arc-list. Depending on the duration or "thickness" of the slice, it is possible that there is more than one arc between a given pair of nodes (or there may be multiple kinds of ties) so it is important to consider how these ties will be aggregated. For most variables, common operations like sum, maximum, count, and average can be used. (Non-numeric categorical attributes will need more sophisticated treatment in the future.) The theoretical framework for the network being visualized will help to determine which is most appropriate. For example, if the weights of ties in the network describe a rate, summing the weights might not be appropriate (unless the aim is to express the network as a rate of change of rates). Using an average value would probably give a better representation. If events in the network represent individual occurrences, flows, etc., and the idea is to explore the totals for each relation, summing the ties is a good option. However, there are other things to take into consideration. If the variation between the max and min tie values is very large (more than one order of magnitude), it may be necessary to compress the range so that both large and small variations of the network will be visible. Using averaging naturally tends to reduce the range, where summing expands it. Another option is to disregard the weights of the events entirely, and just concentrate on their frequency by using the count of ties.10
To capture the changes in a network over time, a series of slices can be used. The appropriate number of slices and their duration depends on the network of interest. Obviously, the questions raised are similar to the sampling questions of data collection.11 One could lump all the data together into a single network by rendering the slice duration equal to the entire observation period. Conversely, one could step through the network in tiny increments, so each new tie can be examined as it occurs, by rendering the slice duration equal to a minute fraction of the observation period. The ability to generate a "new" network at any point along the data's timeline is quite helpful in an animation. Unlike the bins of a histogram, the successive network slices can be allowed to overlap to some degree.

We have found it useful to generate networks using a "sliding window" that incrementally moves a slice of certain width along the timeline. The window functions like a rolling average, adding a few new ties to the front of the slice and dropping the old ones as the start and end times are incremented by a small delta. This has little impact when the underlying data has been collected in discrete waves, but using the sliding window on "streaming" data makes it possible to pull out successive networks that differ by only a few ties. This makes the task of generating geometrically similar layouts much simpler (see discussion of layout techniques below). Letting the bins overlap can be thought of as a crude way of allowing events to "decay" or act as if they have a limited duration or window of effect on the network. One problem with the overlapping slices approach is that it may become unclear where a slice is "at" on the timeline. We chose to measure times from the "back" (oldest/smallest time value) of the slice. Another problem with overlapping slices is that it makes statistical analysis challenging because successive slices share data and are not independent, although, presumably, any kind of successive slices in a network would violate independence assumptions. Deciding the appropriate values for the slice width and delta is difficult, and often requires some experimentation as well as clear thinking about the timescale issues discussed earlier. Some important things to consider are the sampling period of the data, the rate of sampling, the rate of change in the variable, and the rate of change in the network.
V. Social Cartography
The field of network visualization is not particularly unified or comprehensively theorized. It might be described as a set of useful but ad hoc methodologies specific to various problem domains. Although recent increases in computing power and media technology have led to considerable advances over the original sketches made on paper, the size and complexity of the datasets under consideration has also increased, thereby creating dramatic challenges for data presentation (Pajek; see Batagelj 1998, 2004). While we do not have a polished theory or general classification scheme to present, it does seem worthwhile to consider what our aims are in creating pictures of networks, and how they might relate to some of the issues we have described above.
As with any visual representation, visualization of network data serves multiple purposes. Often, the framework used to conceptualize a problem is closely related to the shared metaphor that is used to describe and communicate about it. Enhancing the power and flexibility of visualization techniques can increase our intuitive understanding and ability to communicate abstractly about networks in general. At the same time, visualization can provide a means for understanding specific networks by presenting their data in media that are sufficiently visually accessible to give purchase for intuition, and sufficiently accurate to allow substantive comparison and argument (Tufte 1983).
Ideally, network visualization might serve a role similar to geographical cartography—whose strengths and limitations are well understood and techniques so widely used that they are transparent, allowing us to concentrate on the relationships revealed rather than the tools used to present them. However, like geographical visualization or any charting procedure, network visualization has the power to distort as well as to inform.
The cartography metaphor can be usefully extended to explain some of the problems of network visualization. Maps serve to communicate information about the relationships and distances between geographical entities by discarding some information in order to convey a larger abstraction. Many kinds of distortion occur during this process. Generally, a change of scale is used to compress detail in order to give a degree of overview larger than a single person's perspective. The world is three-dimensional and built on a curved surface, and maps generally must represent such a reality on a two-dimensional static printed page. In order to make this compression possible, choices must be made about which geometric relationships to preserve, and which to discard or distort. The comparison of cartography to graph drawing is useful because many of the same decisions must be made when designing and assessing graph layouts. The abstraction process used to generate a map is not straightforward. It only seems obvious in retrospect because various conventions have evolved about how data should be presented. Different map-making techniques employ different projections. Nautical charts, for example, are drawn to preserve the angular relationship between objects depicted, making it possible to directly extrapolate sightings and bearings. But preserving angles introduces some error in the areas of regions (e.g., Greenland on most world maps), the shapes of coastlines, or distances as measured on the map. Some maps attempt to preserve x-y distance relations, but must discard elevation information or convey it iconically by using contour lines and shading (figure 6a).
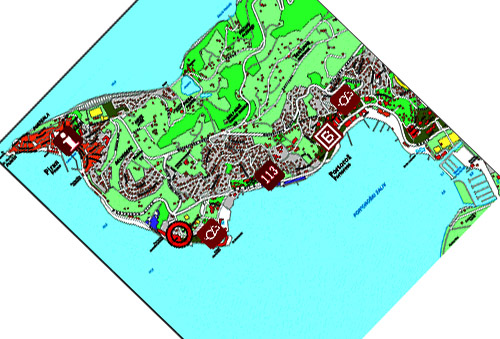
Some maps use a perspective or birds-eye approach to convey information about three dimensions in a two-dimensional plot, but at the cost of obscuring some less important features (figure 6b).12 Maps of subways and transportation systems often drastically distort geometric relations in order to highlight the topology and connectivity of the system. Shading, colors, labeling, and icons are often used to emphasize the textural or conceptual features deemed important by the mapmakers, or to show features that might otherwise be suppressed by the selected layout technique.
Similarly, when constructing a map of a network, we must select a suitable organizing principle and choose which relationships and structural properties are the important ones to display from among the multitude present in a high-dimensional network. Should we choose a technique that emphasizes divisions into clusters and communities, or one that preserves as well as possible the path-distances between nodes? Do we want to highlight nodes’ relative centralities, their attributes, or their age? Do we want to view the network from the perspective of a particular node? Clearly, it would be useful to have a broader catalog of cartographic techniques for expressing network relations in systematic ways, with some degree of classification. This will require work drawing on the expertise of multiple fields: social network analysis, graph drawing, data scaling, genealogy charts, matrix analysis, ecological food webs, gene linkage software, organizational charts, software structure (UML) diagrams, to name but a few (see Di Battista and Eades 1994 for review). Much of the necessary work has been done, but the research communities remain somewhat disconnected such that each has its own criteria for what constitutes a "good" layout. Perhaps the most crucial element is to express to the viewers what the layout procedures are, and what they need to know to "read" the maps critically. We have found the following criteria useful to consider before creating network visualizations:
- What is the underlying set of relations we are interested in, and how can they be best expressed?
- What is the functional relationship between collected data and relations of interest?
- At what time-scale are the patterns of interest likely to be visible?
- What set of transformations do we need to apply to get from the data to a consistent social space?
- How might node and arc attributes relate to the pattern of network structure, and how can they best be translated into display variables that highlight and explore these relations?
Network visualization must deal with the same problems as cartography, but with some additional challenges. First, there are many possible concepts of "social-space" with different theoretical backings and implied relations (Monge and Contractor 2003). Second, when network data is conceptualized as a social space, its "natural" dimensionality may be far higher than the three or four used to describe physical space. Third, raw network data may contain contradictions, infinite or null relations, and asymmetries that require transformation before they can be meaningfully expressed as a social distance. For example, consider the situation of four nodes, all connected with arcs of length one. If we wanted to draw a map such that the screen distances correspond to the arc lengths, we could easily place the first three in an equilateral triangle, but to present all nine relations without distortion, we would require a third dimension so that we could create a tetrahedron. Alternatively, we could place the nodes on a square, but this requires distorting the lengths of the diagonal relations. The number of dimensions needed to describe a set of variables in a metric space so that all of the (symmetric) distance relations are distortion free is usually called the “embedding dimension” (Freeman 1983). In a worst-case scenario, the embedding dimension of the network can be as high as n-1, where n = the number of nodes. Fortunately, most social networks are quite sparse, so their adjacency matrices have fewer embedding dimensions than n-1. However, nearly all will have an embedding dimension greater than the three we can easily conceptualize, not to mention the two that will fit in print.
In cartography there are many situations in which the distortions are minor enough that they can be ignored. The same may be true for social networks. However, it is well established that the positioning of nodes on a layout has a large impact on the intuitive conclusions the viewers will draw (Blythe et al. 1995; McGrath et al. 1997). As has often been suggested in the graph layout literature, it would be useful to have objective criteria on what constitutes a good layout (Davidson and Harrel 1996). Lacking such a measure, it would be convenient if layouts attempting to map network distances to screen distances used a measure of distortion induced in the process of "flattening" the network from its embedding in an abstract social-space to its presentation dimensions. Since the process we are describing here is essentially that of Non-Metric Multidimensional Scaling (Kruskal 1978), a modified version of Kruskal's "Stress" function seems appropriate in some cases. This works by comparing the matrix of "desired distances" between nodes to the actual screen distances produced by the layout.13 Additional exploration of suitable stress measures is needed.
We should emphasize that the stress metric should not be thought of as a measure for evaluating when an image does a good job of communicating the network structure. Kruskal’s stress function only assesses the level of distortion from the distance matrix (however it is constructed), not the optimization of the algorithm or important aesthetic criteria like line crossings, etc. This distinction is important because some algorithms (in particular Fruchterman-Reingold 1991 and Peer-Influence by Moody 2001) are not working to optimize the second- and third-order distances, only direct ties and node spacing. Although this is not well expressed in the stress statistic, we found it useful to make this clear in the Shepard's plot (in which geodesic distances between every pair of nodes is plotted against their scaled screen distance) by using color to distinguish between the first and nth-order distances. The idea is that if one can develop a measure or procedure to map network data to a high dimensional “object” in social space in which the important network or data-relationships are expressed, then the stress measure will tell how well the two-dimensional “shadow” of this object on the page preserves the distance relationships.
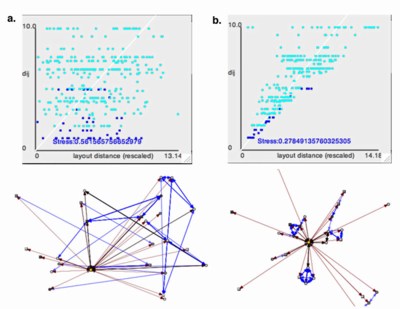
Of course, a large stress value does not necessarily mean a graph is useless. Two-dimensional maps of the world are widely used to convey geographic relations despite the presence of drastic distortions caused by squashing the globe flat. And in some situations conveying topological features of the graph (symmetry, lattice construction), or the relation of nodes, may be far more important than arc-distance correspondence. Although a low stress level may be helpful, the relationship between the distortion in the underlying layout and its ability to communicate the desired pattern of relationships is not straight forward, especially when animation and multiple layouts are involved.
VI. From Network to Social Space
The conceptual framework we propose for network visualization is intended to be general enough to work with many kinds of networks.14 To this point, we have discussed how different forms of longitudinal network information can be used as input for static and dynamic network visualizations. Similarly, we find it useful to separate the modeling of the input data from the modeling of social space in which a network is embedded, and from the operation of the algorithms used to construct images of these spaces. Hence, we next consider how an adjacency matrix is represented in social space.
Most kinds of network data require transformation before they can be visually represented in a two-, three-, or n-dimensional social space because the properties of Euclidean distances measured in the coordinate frameworks we work with in the physical world (or in our electronic representations of it) may not hold true for network distances. The following details need to be considered when constructing a “projectable” social space, although spaces for most data do not really require complete definition because some of the problematic questions may not occur in the context of a given kind of network. First, if the goal of a layout algorithm is to place nodes in a coordinate system so that the distances between them are proportional to the distances between them in the network, then we need to be clear on how we measure network distances. A very common metric is geodesic-distance, or path-distance. This is usually defined as the length of the shortest path traversed along network's ties between two nodes. This definition is quite straight-forward for an un-directed network in which all ties (edges) have equal weight, but it becomes more complicated when these restrictions are relaxed. If the network has directed ties (arcs), then one needs a method to deal with asymmetry before a layout can be constructed. Coordinate systems usually require symmetric distances, so that the distance from A to B is equal to the distance from B to A independent of which node you start with when making the measurement. However, in directed networks it is quite possible that there is a path directly linking A to B, but for B to reach A, the path must go through several intermediaries, and therefore have a different path length. Most layout algorithms ignore this issue and symmetrize the network (usually with max value) before calculating distances between nodes.
Arc-lists or adjacency matrices only define the immediate first-step relations between nodes. In an adjacency matrix, nodes that share a neighbor but lack a direct tie will have a zero or a default value for their distance. These entries must be filled in so that distances between all pairs are defined. If the desired metric is geodesic distance, this can be done using an All-Pairs Shortest Path algorithm (Djikstra 1959), but in cases where the “arcs” of the network are an abstract transformation of data and the concept of measuring distances “along” arcs seems inappropriate (co-occurrence or similarity data) other techniques and algorithms are also useful (Schvaneveldt et al. 1988; Chen and Morris 2003; Borg and Gronen 1997).15
A network may have weighted ties rather than a unit distance for each tie, in which case the weights must be included in the symmetrization and the weighting scheme may need to be transformed. Weights in networks can be understood as a measure of similarity (larger values mean more similarity and therefore closer placement on the layout) or dissimilarity (larger values mean more distant placement). Most social networks use similarity measures (e.g., stronger friendships, larger trade volume, more contacts), which means they must be transformed to dissimilarity before the distance can be calculated. In order to ensure that this transformation is consistent across all the networks in a dataset, we use the transformation equation [(1 / tieValue) * maxValue], where maxValue is the maximum tie value in any of the slice networks (after aggregation, excluding infinity). This reverses the network, exchanging large and small values so that they can be interpreted as distances.
The weighting scheme also needs to take into account the possibility for multiple or multiplex ties.16 Although they are not permitted in a classic graph-theory definition of a network, many networks allow a pair of nodes to be connected by more than one tie. Multiple tie situations are especially likely to arise in time networks with long duration slices. We discussed this in the earlier section on slicing, but we generally use a simple aggregation technique (e.g., summing, averaging, or taking the maximum value of the tie weights). An interesting question for a social space model is the idea of negative relations (see for example, Papachristos 2004). If nodes have a particular default distance, then perhaps negative ties could increase this distance. But should nodes connected by a negative tie be placed further apart than if there was no connection between them? How should the negative weight be included when calculating distances? For example, if nodes are connected indirectly with a geodesic distance of 3 but directly connected with a tie of -1, what should their distance be? In a real coordinate system, the path distance between two points cannot be less than zero. So if negative tie values are permitted, it is necessary to ensure that this possibility is removed. Negative values are often conceptualized as repulsion, but it is difficult to see how to operationalize this for a layout trying to converge on a static optimum for a particular frame. Perhaps this is an appropriate element to consider in future dynamic layout algorithms.17 A recommendation is to treat negativity as an attribute, coloring or dashing the arcs accordingly, and using the absolute value of the weight.
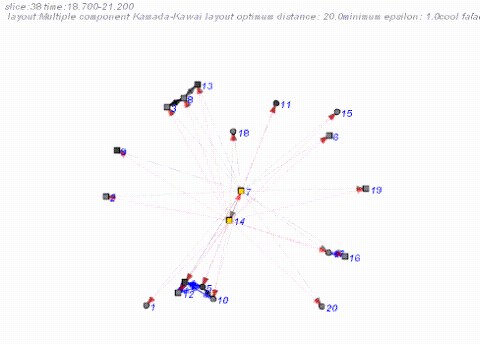
Another issue that complicates distance-representations are isolates and disconnected components: Purists of graph theory seldom take into account disconnected components, or groups of connected nodes with no path linking them to the rest of the network. However, we find that whenever observed event data is aggregated into longitudinal networks there are many such instances. Both isolates and disconnected components cause problems for calculating distances because the lack of connection is interpreted as infinite distance. One way of dealing with this is to run a layout algorithm on each of the components individually (see the multi-component Kamada-Kawai technique below), although this still leaves the question of how the components should be placed relative to each other, and does not necessarily prevent them from overlapping. Another way of dealing with this is to place isolates and components in an arbitrary arrangement. This is an option we have used for isolates, positioning them in a row or circle from which they move to join the network when connected. Another possibility is to temporarily construct ties to attach the isolates or disconnected components with pre-specified distances. This seems to work well but can greatly increase the computational overhead (the additional ties make the graph very dense) and may distort the layout of the components somewhat. The simplest option is to merely ignore the nodes and leave them in their prior location.
Nodes that "die" or otherwise leave the network can be dealt with in an obvious fashion: making them disappear. But when nodes enter the network they may not have a coordinate assigned and we need a strategy to position them. This means placing them at default location (0,0), placing them randomly or using the included coordinates from the import file (if there are any).18 In many cases, the new node does not cause problems, as it is either dealt with by the isolate treatment, or immediately positioned according to its new ties. One benefit of working with social networks is that even when they have a large numbers of nodes they tend to be fairly sparse. Still, for a network of any size, if density of the network becomes large enough the distortion required to present a two-dimensional metric visualization may become great enough to make it unusable (unless the network happens to be unusually planar and lattice-like). This can be an advantage of doing time-based visualizations: the network's ties are distributed across many individual network slices, and these individual slices may be sparse enough for visualization.
VII. Animating Layouts
There are many ways to visualize network change, not all of which need to entail network graphs. It is a fairly common practice to plot changes in graph-level indices over time. If only a few time points need to be shown, a series of side-by-side static networks may be sufficient to highlight structural changes to the graph ("flip book" or static layout techniques, Roy 1983). Static layouts have some advantages as they are easier to print in journals and allow a certain degree of reflection and careful comparison by the viewer. But network theorists often describe networks as a process unfolding in time (generally with the aid of rapid gesticulations) and so a "movie" or animated network layout is a natural means of presenting such data (McGrath and Blythe 2004).
A ubiquitous technique for conveying a sense of motion in animation is to generate a series of images with gradual changes in the position of elements in the frame. When presented in a rapid sequence, the elements in the image appear to move smoothly because of a “persistence-of-vision” effect. However, to preserve the illusion of motion, it is helpful if the elements behave realistically. Sudden large changes of position (or rapid acceleration and deceleration) tend to break the continuity and make the animation difficult to follow, so one criterion for any network animation procedure is that it generate a set of in-between images that make successive layouts flow in an understandable way.
Animated network layouts have several important design criteria in addition to those of the static versions. The human eye is well adapted to detecting and classifying motion (Gibson 1986). This makes animation a powerful tool because, if done well, it allows the natural tendencies of our perceptual hardware to aid in the intuitive analysis of the data, detecting areas of interest, relative rates, outliers, etc. But at the same time, for the mind to be able to maintain a "mental map" (Branke 2001) of the transforming structure, it is important that extraneous or "noisy" motion be minimized to avoid confusing or misleading the eye. In other words, the magnitude of the motion and position change between two successive layouts should reflect the magnitude of network change. This means that in some cases it may be necessary to avoid "over-optimizing" a layout. Reshuffling all of the node positions may allow minimal distortion in a single static layout, but possibly at the cost of disturbing the smoothness of a sequence. On the other hand, when major structural change occurs in the network, sticking to the old positions might be misleading and a reshuffling may be in order. Finding a balance between the two can be challenging.19
Because viewers will (consciously or unconsciously) intuit the rate of change in the network data from the pace of events on the screen, it is important that "movie-time" be used in a consistent way to avoid creating distorted impressions of network dynamics. Like the dimensions in a conventional map, time should not speed up or slow down without informing the user of a "change in scale."20 For example, the duration of the animation between two slice networks should be proportional to the time interval between the networks in the data. One complication is that the animated motion can be perceived as a series of "real" layouts (in which node positions are governed in some way by the weight of the ties between them) instead of as a graphical trick to maintain the viewer's mental map. This suggests two possible methods of interpolating between successive networks:
- Create a layout for each network, and then create a series of "tweening" images of the network in which the nodes' layout coordinates are interpolated to create the impression of a gradual transition from the first to the second.
- Create a series of intermediary "interpolated" networks, in which the values of the arc weights are interpolated and the layout algorithm reapplied to generate the intermediate images. (This would require a very stable layout algorithm.)
The layout interpolation we have found most useful is a slow-in, slow-out technique achieved by using a sinusoid function (Yee et al. 2001) to interpolate the x and y coordinates of each node between the two layouts. One disadvantage of the approach is that nothing prevents nodes from crossing under one another when moving to a new position and, if the positions happen to be on opposite sides of the layout, the transition can be visually confusing. However, good layouts can dramatically reduce the amount of movement needed, making this a very effective approach.
Animation, especially of continuous time data, brings up some questions about how to handle the changing attributes of nodes and arcs, and especially nodes that enter or leave the network. Because of the desire for a great deal of flexibility with respect to how network events are displayed and animated, we structured SoNIA so that the visualization and "rendering" of network graphics takes place somewhat independently of the underlying layout slices. What is actually drawn to the screen is a "render slice" which is constructed from the same underlying data as the "layout slice" (network) but need not have exactly the same time or layout coordinates. The process works as follows: When asked to draw a network to the window, we query the full set of data, looping over all the node and arc events and placing them in the render slice's bin using the same interval definitions as when constructing layout slices. After the render slice has been constructed to include all node and arc events during a given interval, then coordinates for each of the present nodes are obtained from the current network layout. If no layout has been applied, then the default coordinates can be those from the original file. 22
“Tweening” animations are created by generating a user-specified number of render slices. The number of these slices controls the smoothness (and indirectly the speed) of the animation. Generally, the render slice has the same duration as the slice of data used to construct the network, and it functions as a sliding window on the data moving from the start slice until it coincides with the ending slice (see figure 8).
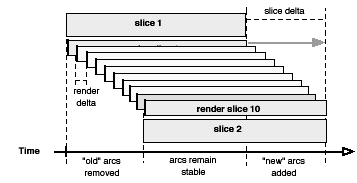
Because the original disaggregated event data are queried to construct the render slices, arc additions and deletions (or changes in color, labeling, etc.) are added to the render when encountered by the slice, and removed when passed over. This makes detailed animation possible, and in streaming data the order and relationship of the tie changes between the two network slices will be visible. However, when the slices have some duration to them (i.e., the network slices have been created by aggregating a period of data) this can create a kind of paradox, highlighting the discrepancy between "real data time" and "interpolation time." Specifically, if the second (destination) network layout contains arcs that occurred quite late in the interval, then they will not be drawn until close to the end of the transition. Nodes affected by an arc change will appear to "lead" tie changes, so that nodes will approach each other in the graph before their tie appears.
This paradox is caused in part because thick slices describe an interval in time rather than a point. Therefore, there is no clear logic for where the network layout should be "positioned" on the timeline relative to the interval. We made a convenient but somewhat arbitrary choice to consider the network to be at the start (the left-most, smallest time-value) boundary of the slice. This placement should be reconsidered or made an option in the future. Also, the option should be given to draw all of the slice's ties at once, eliminating both the detail and lead-lag problem.23
Most network visualizations use graphical attributes and labeling to iconically convey information about the underlying data. In most cases the viewers are not interested simply in the structure of the graph, but in how the structure relates to predictive or dependent variables (e.g., preferential attachment, attribute bias, disease transmission). A carefully chosen mapping of variables to attributes can highlight these relations, but there is always the risk of confusing or misleading the reader into interpreting the color codes too literally.
To partially address these concerns, we took advantage of Java's graphics capabilities that make it possible to have semi-transparent arcs, and produce high-quality anti-aliased images. Semi-transparent arcs are useful for conveying the presence of multiple arcs (additional arcs will make arrows appear darker) or multiplex ties. In addition, if consideration is given to how arc colors are mapped to arc attributes, the hues resulting from overlapping arcs can be interpreted meaningfully.
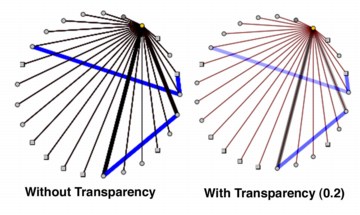
RGB values specify the strength of the red, green and blue color components by a real number between 0 and 1. This means that continuous attribute variables can be mapped to the colors, not just categorical ones.24 For example, in McFarland's classroom data the ties can be described as having "task" or "social" content, and positive, negative, or null emotive valuation (McFarland and Bender-deMoll 2003). Mapping "social" to the blue component makes the blueness of an arc an indication that the relation is social. Mapping "sanction" to the red component makes the redness of the arc an indicator of the degree of sanction. Because the colors are on independent perceptual “axes,” interactions that are social and sanctions will show up as purple, and arcs that are only task-oriented will show as black. This can be particularly effective when semi-transparent arcs are layered, as the combined colors yield intermediate hue gradations that are still readable. Use of semi-transparent color may help to counter a frequent criticism of visualizations—that overlapping arcs make it difficult to use the balance of color as a reliable indicator of the balance of tie types. Java’s transparency and compositing abilities also facilitate the "ghosting" feature, in which a light image of the previous layout is retained behind the new layout for comparison. This is useful both for fixed position "flip-book" animations and as a tool for debugging the motion of nodes on a layout (Moody, McFarland, and Bender-deMoll 2005).
Because there are so many parameters and options in creating an animated network layout, it is important that there be a way to store or save an animation so that it can be referred to later or shared with other researchers independent of the software used to construct it. SoNIA provides the option to export an animation as a QuickTime movie file.25 QuickTime is designed to play files back at a constant rate, ensuring that the time-scale will remain constant and not speed-up or slow down with the number of entities on the screen. However, the format is based on compressed bitmap images rather than vector graphics, so files are large and quality degrades if images are rescaled. As in any digital movie, there is always a trade-off between file size and image quality. In the future, we hope to explore the possibility of writing vector-based animation files, such as Macromedia's Flash (.swf) file format. SoNIA includes the option to export a text file containing the set of matrices (after aggregation, etc.) corresponding to each layout slice. This makes it possible to import the networks into a package like R (R Foundation), UCINET (Borgatti et al. 2002) or SIENA (Boer et al. 2003) to calculate a time series of descriptive statistics or other substantive analysis. Unfortunately, SoNIA does not yet include the ability to save out data in other network formats, or even in its own .son format.
VIII. The Layout Process
In creating SoNIA, we attempt to fit various layout techniques into a common framework, making possible independent exploration of the stages of the layout process.26 We identify five main elements to the layout process that seem applicable across algorithms: The initial starting coordinates for the network, the treatment of isolates, the level of visual feedback from the running algorithm, and the transformations applied to the layout after the nodes have been positioned.
Because many of the algorithms use optimization procedures to arrive at a set of node positions, they require an initial set of coordinates as a starting point, and in some cases the choice of initial positions will greatly shape the final layout. For some networks, there may be a "natural" set of coordinates from which to start—perhaps geographic, derived from a theory, or the result of another algorithm. If these coordinates are included in the input file node definitions27 they can be used as starting positions. Using a consistent set of starting coordinates for each frame can have several advantages, especially when there are a number of isolates or disconnected components. If the isolates are not explicitly dealt with in another fashion, the file coordinates can act as a resting position that becomes familiar to the viewer.28
Using set starting positions can be useful when you want to be able to regenerate a layout exactly29 or test the effect of other layout parameters. Starting the nodes from a circle works well because nodes are often pulled in towards the center, and components are somewhat less likely to overlap. Randomized starting coordinates are often a good idea as a check to make sure that pre-conceived structural notions are not overly influencing the layout. Random initial positions are also useful for testing the stability of a particular layout configuration by comparing multiple runs.
However, repositioning the nodes randomly for each slice tends to result in layouts that are less stable over time, and wastes computation resources because every layout has to start from an equally bad configuration. In contrast, for Fruchterman-Reingold and Kamada-Kawai algorithms, fairly stable results can be achieved by "chaining" the layouts, starting each one from the coordinates of the previous (Moody, McFarland and Bender-deMoll 2005). If there is little change in the network between the two slices, the algorithm may have little work to perform in order to find new optima, and it is likely to be fairly close spatially to the previous ones. However, there may be an increased chance of remaining stuck in local optima. There is also the option of starting a layout from its current screen coordinates. This makes it possible to run a layout after manually adjusting node positions, or if an algorithm needs to be re-run after exceeding the current limit of iterations.
Handling isolates elegantly will probably be the detail that makes or breaks a layout technique. We have explored several options with moderate success. Ironically, the technique that seems to be most effective is to ignore them, leaving them where they were last positioned by their ties.30 Initially it seemed like a good idea to have the nodes retreat to the periphery (positioned either in a circle around the layout, or in a "penalty box" at the bottom) when they become isolates, but if there are very many entrances and exits the movement can become quite distracting unless the focus of the visualization is the integration of isolates. In addition, some care must be taken because the isolate positioning scheme has the potential to influence the final layout when isolates are re-connected and drawn back into the network.
There are many possibilities for providing feedback while the layout is running. The most effective is to monitor the algorithm's progress by redrawing the network after every iteration. This option is helpful for testing algorithms or adjusting parameter settings to an optimum. However, it is also the slowest option because of the time needed to update the screen after every iteration. Compromise is possible by setting redraws to occur on every Nth pass through the algorithm. A less costly option is to provide the user with an animated time-series of the algorithm’s parameters, or even more effectively, the rate of change of these parameters in order to allow rapid assessment of convergence. Feedback on the Fruchterman-Reingold and Kamada-Kawai algorithms' convergence is presented using the "cooling schedule" window (see below details for each algorithm).
Depending on the network and parameter settings, it is often helpful to transform the completed layout. This must be done with a bit more care for a set of network slices than for a single static layout. If every slice is independently rescaled to fit, then the hard-won consistency in screen distance will be discarded. Re-centering is generally less problematic, but outliers and un-positioned isolates can cause some "drift." (We included an option to ignore isolates for re-centering,31 and found it useful when the isolates are pre-positioned.) In SoNIA, we used the screen pixels as the coordinate base. This means that the origin is in the upper left, and negative coordinate values place nodes off the screen. Some layout options will automatically rescale graphs to fit, but the coordinate framework needs additional consideration in future work.32 It seems that a better solution would be to keep the screen and layout coordinates independent. The layout algorithms would operate on whatever the natural coordinates of the data are, and then a user-specifiable zoom, translation, or rotation transformations could be applied to fit the network on screen, allowing greater flexibility without modifying the coordinate data. For an elegant explanation of this, see the discussion of “space-scale diagrams” in Furnas and Bederson (1995).
In our experience, a good general procedure for working with a network is to tweak the chosen algorithm’s parameter values until reasonable results are achieved for one slice, and then to run the same algorithm automatically on the subsequent slices of the network. In some cases the topology of the network will change enough over time that the original settings may not give good results for the entire time sequence, in which case the parameters can be changed and the process repeated. It is a good idea to make sure that the same settings are applied to the entire network, or it will be very difficult to repeat the layout later. It is worthwhile to evaluate the stress of the layout at multiple points to check that the layout is still reasonable when densities of the network change.
We found that in some cases the processes cannot be completely automated because an algorithm will fail to completely converge on a layout for one or more slices in the sequence. When the procedure is to chain the layouts (start each one from the coordinates of the previous) this will most likely influence the results of all subsequent layouts. We often found it necessary to return to the problem slice and adjust the parameters or tweak the node positions slightly. Usually after minor modification it is possible for the layout to converge and continue, reapplying the process to later layouts. Perhaps this process could be automated in the future by essentially adding a small amount of “noise” to problematic slices.
IX. Evaluating Layouts
Although we do not have any comprehensive means of assessing the suitability of a layout, there are some ad hoc procedures and criteria that we believe can improve the accuracy of network visualizations. Some of these criteria are presented below.
One of the most basic is to construct layouts that are well documented and replicable. We found that a key element is to automatically generate a log file that records the parameters and results of every command applied to the network. If this file is saved along with the network movie, it is possible to reconstruct the layout, or the file can be consulted to determine the appropriate text to include in figure captions and explanations. This step of reporting the layout procedure and an assessment of the accuracy of the image is often neglected when network graphics are employed and often results in confusion about how the image should be interpreted.
Ideally, every image of a network that appears in print should be captioned with the layout parameters in enough detail that a viewer could independently reproduce the image in similar software. In fact, if the information has been presented with minimal distortion, it should be possible to reconstruct the relevant elements of the original data-set (which nodes are connected, and how strongly) purely from its graphic representation. We would certainly expect this degree of accuracy (the ability to "scale" data from the points of a plot) from most scientific figures. In practice this is rarely feasible.
Part of the power of visualization is its ability to show information so that our intuition can gain a purchase on it. But until we have a well-understood equivalent of a "p-value" or an error term to give the viewer, we need to provide viewers with all the information we can to help them determine the validity of our claims. Including the results of the stress calculation may provide an error term of sorts, but it will probably only be applicable to a fairly narrow range of layout strategies.
There are several levels of concepts that we have found useful in discussing the accuracy of a layout and the dependability of software. We have been using the term “layout repeatability” to mean “ability to produce the same result given fully specified starting conditions.” Given the same data and the same settings, do we (or other researchers) get the same results? Obviously the first step to achieving this is to have clean, bug-free code.33 Repeatability also means making sure the program reports all its parameters, seed values for random number generation, and so forth.34
We use “layout stability” to mean the "ability to produce the same layout independent of minor changes in parameters or initial conditions.” We argue that, in most cases, for a layout to be considered reliable it should not be fragile or arbitrary. In other words, the features of the data that may become apparent in the representation should not be overly dependent on the settings used to generate the layout and they should look more or less the same even if viewed from a slightly different "angle." Unstable layouts can indicate bad layout algorithms, an algorithm which is not appropriate for the data, or that the underlying data are so noisy, fast-paced, or high-dimensional that a good representation is difficult to achieve. However, it is also the case that for a particular set of nodes and arcs there are often multiple layouts that are equally "accurate" representations. These alternate "isomeric" layouts (indicating multiple stable configurations) should be distinguished from truly unstable results.
In theory it should be possible to test the stability of layouts fairly systematically. For the layout parameters, this can be done by perturbing the values by small amounts (a few decimal places), re-running the algorithm, and observing the resulting changes in the layouts. If the configuration is radically and/or unpredictably different when compared to the original layout, we should conclude that the layout is unstable, and that we should be cautious about its utility. A related technique is to compare the results of multiple layouts run with random starting coordinates. Because many of the layout algorithms rely on minimization strategies to improve the layout from its starting coordinates, they can be very sensitive to the initial positions of the layout. Randomizing the nodes’ starting positions can provide a rough assessment of this sensitivity.35
In order to make assessments of stability and repeatability, we need some criteria for comparing layouts. We define “layout comparability” as “the degree of position matching between two independent layouts of the same network.” This definition is something of a cop-out, as it does not specify the metric to be used in position matching. Two possibilities for measuring the similarity of nodes’ positions between two layouts:36
- A sum over all nodes of the Euclidean distances measured between the coordinates of each node and its alternate position.
- The number of non-matching nodes, where a node is considered matching if the coordinates of its alternate position lie within some small threshold distance.37
In our experience, most of the existing network visualization packages perform very badly on all three criteria, although stability depends largely on the structure of the network and algorithm used. SoNIA was designed with these elements in mind, and, at least for the KK layout, gives somewhat better results for reliability and stability. However, even if the necessary elements are in place to achieve repeatability, the number of parameters that must be accurately specified to achieve identical output is large enough to make it difficult to achieve in practice when communicating with another researcher. This is an important issue that future work must address.
X. Details of Specific Algorithms
We have implemented several commonly-used network layout algorithms in SoNIA, and worked with them to do dynamic visualization with varying degrees of success. These approaches may be found sub-optimal in the future, but they are the ones we have chosen to concentrate on to date. They are also somewhat familiar in the social network analysis community from their implementation in Pajek. The algorithm that seems to give the best general results is the Kamada-Kawai (KK) spring-embedder layout (Kamada and Kawai 1989). We had relatively good success with the Fruchterman-Reingold (FR) force-directed layout (Fruchterman and Reingold 1991). Further work is needed on our version of Metric and Non-Metric MDS, and further experimentation is needed on the Peer Influence (PI) algorithm proposed by Moody (2001). All of these algorithms differ not only in their optimization techniques but also in their implicit models of social space. Both the KK and FR algorithms require some interpretation for implementation as some of the specifications were not explicit in the papers, and some extensions were needed for our uses.39 For the purposes of this paper, we focus our discussion on KK and FR algorithms and present a summary table characterizing others (see table 1 for a summary of algorithms currently considered in SoNIA40).
Much of the initial structure is in place to allow a fairly comprehensive comparison of layout techniques, but many more of the existing published algorithms need to be coded before we can argue that we have made a thorough exploration and classification of techniques. Our general conclusion is that these "standard" algorithms used in social network analysis are relatively old, so additional work should be done to integrate algorithms and recent research in domains such as energy minimization, constraint optimization, and dimensional projection. For example, extensive work on visualizing large networks and projecting from higher dimensions has been published in the graph drawing literature41 and needs to be integrated into social network analysis.
| Name | Input Matrix | Model | Optimization |
|---|---|---|---|
| Kamada-Kawai (KK) | All-pairs-shortest-path measure of distances between nodes. | Springs between all pairs that relax to edge length. | Each node has an "energy" according to its "spring tension.” The energy of a network is minimized by iteratively moving the node with highest energy to optimal position using a Newton-Raphson steepest descent. |
| Fruchterman-Reingold (FR) | Raw distance matrix. | Electrostatic repulsion between all; attraction to connected nodes; force minima is at desired edge length. | Reposition nodes according to the force vector they "feel." The distance nodes are allowed to move is gradually decreased until graph settles. |
| Peer Influence (PI) | Raw similarity matrix. | Nodes are repositioned to the weighted average of their peers' coordinates | Repeated iteration. |
| “Classic” Metric Multi-Dimensional Scaling, “Spectral” techniques (Metric MDS) | All-pairs-shortest-path matrix or alternate measure of distances / similarities between nodes. | 2D projection of high-dimensional space of the network using matrix algebra to determine Eigenvectors. | Exact solution, usually based on SVD. |
| Non-metric Multi-Dimensional Scaling (Non-metric MDS) | All-pairs-shortest-path matrix or alternate measure of distances / similarities between nodes. | Search for a low-stress 2D projection from an embedding of the network in high-dimensional space. Stress calculation compares only rank-ordering of distances. | There are many different numerical optimization techniques. |
| “Modern” (metric or non-metric) Multi-Dimensional Scaling (MDS) | All-pairs-shortest-path matrix or alternate measure of distances /similarities between nodes. | Search for a low-stress 2D projection from an embedding of the network in high-dimensional space. | There are many different numerical- and constraint-optimization techniques. |
| Direct Optimization | Various statistics that measure the layout’s properties. | Search for positioning of layout that optimizes specific criteria. | Repeated iteration of simulated annealing or another constraint optimization technique. |
Kamada-Kawai
The Kamada-Kawai algorithm is commonly described as a "spring-embedder," meaning that it fits with a general class of algorithms that represents a network as a virtual collection of weights (nodes) connected by springs (arcs) with a degree of elasticity and a desired resting length. The problem then is to reposition the nodes until all the springs are as relaxed as possible. Kamada and Kawai's version utilized simple force equations and a Newton-Raphson steepest decent approach42 to locating the optimal configuration. In addition, they perform an All-Pairs-Shortest-Path distance calculation to determine the desired spring lengths between nodes. Interestingly, because the KK algorithm is working to optimize distances between every pair of nodes, this makes it formally similar to a “modern” metric multidimensional scaling approach (Krempel 1999; Borner et al. 2003). Because we have adapted the algorithm to work with weighted digraphs and the possibility of multiple components, some transformations (transformation to dissimilarity, symmetrization) are usually necessary. When there are disconnected components in the graph, the algorithm is run independently on each.Kamada and Kawai give details of the algorithm in their paper (1989), but we offer a summary here. First, the algorithm calculates the "energy" (sum of spring tension) for each node. It then loops over all the nodes to find the one with the highest energy (worst positioning), and begins iterating the Newton-Raphson stage to compute new positions for the node until its energy is below epsilon (the target parameter). At this point, it again looks for the node with the highest energy and begins moving it. This process continues until there is no node with energy above epsilon.
This procedure needs several extensions to work for our purposes. To get an optimal layout, the epsilon parameter must be set to the minimum (lowest energy) possible for the graph, but there is no simple way of determining this before running the algorithm. If the value is set too low for a particular graph, the algorithm will not stop unless a maximum number of iterations is exceeded. But this gives no guarantee that the user will acquire a good layout. It is possible for the layout to enter a loop, where positioning one node worsens the position of second, which is then repositioned affecting the first, and so on. In addition, the process of deterministically moving the "worst" node to the best position and then re-evaluating it can be a problematic means of exploring the search space. It is generally more effective to optimize the entire graph incrementally.
SoNIA's version of KK attempts to implement a gradual decent approach to the minimization. The target epsilon is initially set to the energy of the worst node. When the energy of each node in the layout is better than this parameter, the target value is improved (reduced by a fraction, the "cooling factor" parameter) and the algorithm continues until the layout is better than a global "minimum epsilon." This ensures that if the layout exceeds the maximum number of iterations or lands in a loop, at least a basic level of optimization will have occurred. Informal testing seems to show this procedure arriving at better layouts with fewer iterations.
In SoNIA, information on algorithm convergence is provided in the "Cooling Schedule" window by plotting the difference between node energies after each pass.

A well-behaved layout will show a point cloud smoothly converging on the minimum value. This makes it possible to assess whether the parameters should be changed so as to allow additional iterations in difficult layouts. This suggests the possibility of building a "smarter" algorithm that stops when additional iterations no longer improve, but this will require additional testing and parameter tuning.
KK was originally intended for undirected, non-weighted, single component graphs. We took a simplistic extension to weighted graphs, symmetrizing the input digraph and using an All-Pairs-Shortest-Path algorithm to give a matrix of graph distances that are multiplied by an "optimal distance" parameter to give a desired screen distance.43 To deal with the possibility of disconnected components, the algorithm is run independently on each (weak) component with more than one node. This means that there is nothing explicitly separating the components, and they sometimes overlap on screen. Several people have reported some success using a "phantom network" to minimally connect the graph in order to avoid the component positioning problem. This approach sounds promising but needs some additional thought and testing.
Kamada and Kawai argue that their layouts are not influenced by initial conditions, but this may be because their work focused on fairly simple graphs. We have found that for many graphs the results are highly dependent on initial conditions. This seems to be especially true for graphs that are dominated by a "star" configuration. This means that there are many nodes with similar connections and their placement in relation to each other is mostly the result of path dependence in the layout procedure because there is no information favoring a selection among equivalent layouts. To put it in another way, graphs with "truss-like" structures tend to be stable and graphs with lots of points are more flexible, having multiple "isomorphs" with similar stress levels.
We have had the most success with the Kamada-Kawai algorithm, but perhaps only because it is the algorithm to which we have devoted the most time, or because it is better suited to the concepts of social space we are using. There are several strong advantages to the KK algorithm. One is that the Newton-Raphson optimization procedure is completely deterministic: When given parameters and starting positions, it will arrive at the same solution for the same graph. This is convenient when working with a sequence of time-based networks. If we start the layout from the previous slice's node coordinates and there is no change in the arc weights, then there should be no change in node positions. In addition, if there are small changes in weights between the layouts, or a small number of arcs added or deleted, then KK will likely find new minimum that is close in coordinate space to the previous solution. This minimizes node movement and generates layouts that appear very stable over time. One drawback to KK is that the energy calculations in the Newton-Raphson procedure are computationally expensive.
It seems that there are many possible ways to improve results of a "KK-ish" algorithm. One would be to try using a more "true" simulated annealing optimization procedure instead of the deterministic selection of the highest energy node. This usually means that instead of always picking the highest energy node, nodes would be picked with a probability proportional to their energy. And instead of always moving a picked node in the direction of the gradient (towards the local minima) a node is allowed to make "uphill" movements with some small probability that is decreased according to a cooling schedule over time. It is our understanding that this generally results in the convergence on global rather than local optima.44
Fruchterman-Reingold
The Fruchterman and Reingold algorithm (FR) is often described as employing a "nuclear force"45 metaphor: all nodes repel each other, but connected nodes attract. A given pair of nodes is at an optimal spacing when the attractive and repulsive forces between them cancel out. At each pass of the algorithm, the "force" vectors between all nodes are added, giving the displacement and new position for each node. The displacement is limited by a "temperature" parameter that is gradually decreased until no movement is possible.It is important to note that, unlike the KK algorithm, FR does not create a shortest-path matrix. Because all nodes repel each other with increasing force as they get closer, it is unlikely that nodes or cliques will overlap, so there is no need to calculate desired distances for distally connected nodes. Isolated nodes and disconnected cliques can be directly included in FR, but because of the repulsion between them, they will drift further and further apart unless some bounding criteria is applied. Fruchterman and Reingold discuss using repulsive bounds, although the vector math can be complicated for circular areas. We also added a "repel cutoff" parameter (similar in idea to their "grid-variant" approach), which limits the distance at which nodes repel each other, making it possible to avoid dispersing components off the layout. The original FR algorithm was also designed for use with unweighted ties, so we parameterized the "optimal distance" (the equilibrium point k in FR) so that it is scaled according to the weight of each arc.
A major weakness in the FR paper is that they do not give the "cooling schedule" used to reduce the nodes' permitted displacement with each pass of the algorithm. Our experimentation shows that layout success is often highly dependent on the details of this function. In order to explore this, we configured SoNIA so that the cooling function is set up as a segmented curve with movable control points.
The curve gives the fraction of the starting temperature (given as a layout parameter) to be used for each pass of the algorithm, as well as the stopping point.46 It is generally useful to customize this curve for a specific class of networks so as to avoid incomplete layouts or wasted optimizing passes. We have had the most success with monotonically decreasing curves that drop off sharply from a high start, and have a long tapered tail to allow fine adjustments of positions.
Perhaps because it uses only direct ties, FR sometimes seems to create layouts that better express connectivity, while KK seems to create layouts that better express distance. However, in its current implementation the algorithm suffers from some drawbacks that make it difficult to use in dynamic network visualizations. First, as Fruchterman and Reingold mention in their paper, much better displacement equations can be formulated. When SoNIA is set to redraw the network after each pass, it becomes clear that FR causes nodes to dramatically "overshoot" their optimal positions in each step. This is exacerbated by the fact that the positions of all the nodes are updated simultaneously.47 Without the decreasing temperature parameter, nodes seem to bounce back and forth, trading places with little or no convergence. The "bounciness" of the layout creates a great deal of instability across multiple layouts, making animation difficult. Lowering the cooling parameter dramatically can limit some of this, but much "necessary" movement is suppressed as well.
Because of its conceptual simplicity, the FR algorithm is quite promising, but it probably needs to give more stable results before it will be useful for animation. We made several attempts to stabilize the results of the FR algorithm. We were also interested in creating a layout algorithm that made more explicit use of the time aspects of the network data. To do this, we extended the FR algorithm by adding an attractive force between each node and a fixed starting position (generally the location in the previous layout). We label this the “Rubber-Band FR algorithm.” The general idea behind it was to "weight" the previous layout to some degree, encouraging the new layout to converge on a set of positions which were as similar as network structure allowed. This was done by constructing a set of phantom edges, or "rubber bands," to a node's previous location. While the rubber bands reduced the bounciness of the FR animations, the results remained underwhelming. If the attraction was strong enough to stabilize the layout, it tended to add too much distortion. The concept may still be effective if the FR algorithm itself was more stable.
XI. Example of Dynamic Network Visualization
This example is developed from data on repeated observations of social interactions in a high school economics classroom (for descriptions of the larger data set consisting of many such classes, see McFarland 2001; McFarland and Bender-deMoll 2003; Moody, McFarland and Bender-deMoll 2005). The data consists of streaming observations of conversation turns. The conversation turns are recorded as pairs of senders and receivers. Speakers are viewed as directing their communication in one of two fashions: (1) indirect soundings, such as lectures; and (2) direct interactions focused on particular others. Each type of directional speech is viewed as having different forms of network reception; indirect speech reaches all bystanders and directed speech reaches the focal person.
Interactions are also coded for their content or type of tie: task and sociable topics (McFarland 2005). Task interactions are those behaviors that pertain to the ongoing teacher-prescribed task (content is academic). In contrast, sociable interactions involve everyday concerns of adolescents’ social lives, such as parties, dating, social outings, plans, etc. While content is the key distinction, it is often the case that these speech acts are distinguishable in style as well, where sociable behaviors are more play-like, fast-paced, and free than the more constrained academic styles of speech during lessons (Cazden 1988). Last, observations also recorded when task and sociable forms of interaction were laminated with evaluative meaning. Such evaluations were seen as being either positive (praise) or negative (reprimand, see Ridgeway and Johnson 1990).48
We will try to phrase this in the terms discussed earlier in the paper, to demonstrate the processes of constructing a rough data-model for visualization. It is perhaps appropriate to say that what we are trying to visualize for exploration is a classroom attention network, in which proximities and positions indicate the relative focus of the actors. This network is an abstract construct with continuously changing tie values, although there are interesting moments of near discontinuity (McFarland and Bender-deMoll 2003). This hypothetical attention network is relatively fluid, with shifts taking place on a scale of minutes, i.e. orders of magnitude more rapidly than the pace of events in a friendship network. The data that we have for constructing this network are discrete events (directed individual speech acts with continuous time coordinates) that we might argue are coupled in some highly complicated way to the focus of the actor’s attention. In other words, whatever the underlying social process, utterances from Betty to the teacher are more likely if Betty is attending to the teacher (but by “attending to” we do not necessarily mean “on-task”).
Because we want to use weighting to distinguish between utterances, and to aggregate appropriately, we need to have a rough idea of what our units might mean, even if we only care about relative magnitudes. In this case, we use the idea of “face-time.” This permits us to use a simplistic but plausible weighting scheme in which indirect or “broadcast” statements are weighted as 1/n, where n is the number of addressees, assuming that a person talking to a group must divide their attention, and being yelled at as part of a group is not as “strong” as being yelled at directly.
For this data, we have time information on the beginning and ordering of the speech acts, but duration information is not available, so they are coded as “instantaneous events.” For the nodes we have duration information (presence in and exit from class) so they are defined as interval events. In this kind of “mixed mode” network, it is necessary to use thick slices to bin and aggregate the data. And it seems appropriate to aggregate using average, to get the “average face time.”
We depict the interaction in this class period as a network movie using 2.5 minute time slices (average tie value in each slice) and a .5 minute delta. As such, there is a sliding window of 2.5 minutes wherein all observed dyadic interactions are being shown. Below is a screen-shot of the phase-plot (see figure 12). The sliding window (or time-slice) is identified by the pink rectangle. The vertical lines indicate the delta increments of .5 minutes. And the blue dots indicate instances of observed interaction. We select a 2.5 minute time-window because it is wide enough to capture enough of the interaction to represent fluid patterns or network forms (not just sequential dyads), and narrow enough so as to not merge a variety of interaction routines together (e.g., lecture and group work), thereby confounding meaningful configurations.

We developed network movies using Fruchterman-Reingold and Kamada-Kawai algorithms.49 In figure 13, we plot the stress levels generated by the graphical depiction of network distances in each slice. The plot merely shows the stress level of each graph, by each algorithm, and does not reflect how much artificial movement exists across them. The plot shows the graphs’ fitness levels vary. Most of the fluctuations arise whenever broadcasts occur (see movie). Inspection of specific Shepard’s plots reveals that direct ties have much better fitness in these instances.
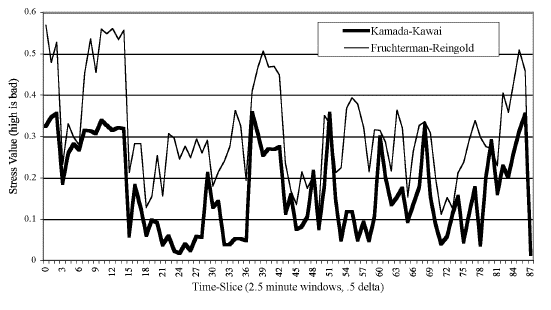
In comparison with the FR graphing algorithm, the Kamada-Kawai algorithm seems to generate graphs with the lowest stress. The FR procedure generates graphs with an average stress value of .31 (standard deviation = .12) and animation across FR graphs generates a great deal of artificial movement. In contrast, the Kamada-Kawai procedure generates better fitting graphs with an average stress level of .17 (standard deviation = .11). This increased fitness also comes across in the movie, which is the greatest approximation to the field worker’s account of social behaviors (and also the most substantive meaning to the observer).
Below, we present the network movie generated by the chaining of Kamada-Kawai generated graphs (see figure 14). In the figure, there are various colors and shapes that have ascribed meaning: yellow squares = teachers; grey nodes = students; circles = females; squares = males; darker nodes = older students. The arcs are depicted in three colors: black = task; blue = sociable; and red = conflict (any negative evaluation). Arrows show arc directionality. Other specifics: We use a circle as a starting configuration upon which to reach an optimum in the first slice; we then chain subsequent graphs by using the prior layout as a starting configuration; and we ignore isolates. Other settings use default parameters.
This particular class (#33) is an economics class composed of 11th and 12th graders at a magnet high school. On this particular day (10/16/96), the economics class has two teachers. The first is the usual teacher and the second is a businessman who donates his time a couple days a month to assist the class with their lesson on stock investments. After a minute of undefined class time, the two teachers prescribe collaborative group work and assist students in conducting it. The students are assigned to groups where they are to collaboratively study the stock market and make mock investments they can follow over time. The aim of these groups is compete with each other over the course of the semester to see who can make the greatest profit and receive a prize. The network movie using KK illustrates the class opening with the teacher trying to focus student attention and then lecturing while the visiting professional assists each group. The teacher prescribes group work but continues to broadcast directives, thereby preventing the desired social routine of group work from taking effect sooner. Eventually the students establish their group interactions while the adults move from group to group so as to facilitate and stabilize interaction patterns.
The routine of group work is basically characterized by dyadic task and social interactions that persist in multiple clusters. Not all persons engage in these groups, and a couple students sit quietly by themselves. The group work routine breaks down as social activity increases within the groups and the teacher emits broadcast sanctions in an effort to redirect student attention back on task (~16 minutes). The task breaks down again at the end of class, but this time because the adults make closing announcements. In such a fashion, the movie shows teachers involved in the task engaging their students as they monitor interaction. When students become too social, a teacher usually arrives, disperses the group, and then reforms it via task interactions. Hence, there is a “dance” here, and it entails relatively bounded groups of individuals that free-associate over tasks and drift into social affairs, while teachers refocus affairs by indirect means of broadcasts and by direct means of directed speech.
XII. Conclusions, Speculations, and Future Work
The past two decades of network research have been characterized by increasing quantitative sophistication. As methods become more specialized and technical, there is greater and greater need for inductive, exploratory tools that enable researchers to more readily intuit and understand social network form, content, and process. Network visualization is frequently heralded as such a tool. In this paper, we continue the public discussion on network visualizations and describe how they can become more than artistic renderings and metaphors for structure (Wellman 1988). To do this, we need to lay bare the assumptions behind network visualizations and describe criterion upon which better or worse graphs can be identified. In this manner, we can bring the art of network visualizations one step closer to science, or at least bring network visualizations under the realm of scientific debate.
In the introduction we presented some frequent criticisms of network visualization. In our work we attempt to move beyond critique to explore some of the underlying issues by developing an open-source software called “SoNIA” that enables researchers to see the underlying parameters of network visualizations and to test them. Clearly SoNIA is a prototype in need of a great deal of work before it will be a useable multi-purpose tool for network visualization.50 However, it seems to be nearly unique in its focus on longitudinal dynamic network data, and we have found it to be both useful and useable.51 If nothing else, SoNIA demonstrates that the animation approach is a feasible and powerful way of communicating the structure of longitudinal networks to viewers.
If we are going to get an intuitive and theoretical grasp of the underlying processes in dynamic networks, we need network visualizations that capture dynamics and generative mechanisms. Dynamic network visualization of these processes enables researchers to explore this untapped terrain, to develop new hypotheses specifically about network theory, and, when changes of time-scale are facilitated, to study the transition points between micro and macro level network processes. However, adapting static layout procedures to dynamic tasks is not a trivial problem, and it would be worthwhile to develop layout algorithms that are specifically designed to work with dynamic data. It is also important to study the perceptions and conclusions viewers draw from the animations and how well these correspond to processes we establish via statistical techniques (Wasserman and Pattison 1996; Snijders 1996; Snijders and Van Duijn 1997; Robbins et al. 1999; Snijders 2001). Additional research on human perception may give clues as to when motion is useful and when it is distracting (McGrath and Blythe 2004).
We argue that a clear concept of how the raw data in a network will be aggregated and transformed to create a stable social space is necessary to create a meaningful visualization. For longitudinal networks, this may require a shift in focus in the underlying data away from static sampling methods to streaming event data wherein generative processes of network formation, change, and dissolution arise (Monge and Contractor 2004). We have described here one possible flexible approach to such network data, treating it as events to be sliced and binned into “networks” on demand. This model of "rolling windows" and slice networks is an effective way of dealing with networks in which nodes and arcs enter, leave, and change their attributes. But it is much less useful when network data are pre-aggregated into waves or matrices. We would like to emphasize the need for researchers to think very carefully about time and sampling issues when recording network data, and the need to work towards more fine-scaled approaches to datasets in general.
But, of course, the model of social space we discuss here will not always work. Many network datasets will be too dense, meaning that they require high-dimensional embedding to create layouts with acceptable levels of distortion within this framework. Exactly where this threshold lies is unclear, and it generates a number of interesting research questions. Does the density level of a network identify when distortion starts to be a problem? Do social networks have geometric characteristics that are different from other classes of networks? How much and what kind of distortion is allowable before a visualization becomes more decoration than information? Are there better stress metrics for alternate models of social space?
SoNIA and the methods presented here are a continuation of research aimed at improving network visualization such that it can be held to scientific standards, and so that visualizations afford both state and process descriptions enabling the science of social networks to develop into a more unified and consistent theory. In particular, dynamic network visualizations seem most promising as they lead scholars to think in an explicit fashion about the role of time in their data and in social structure more generally. Instead of static forms, dynamic visualizations force viewers to see dances, congealing, dispersal, rotations, pacing, alternating forms, etc. From such viewing, the analyst begins to ask what mechanisms generate these processes and regularities over time, and they begin to adopt a frame of mind where social dynamics are front and center.
References
AT&T Labs-Research. 2003. "Graphviz: Open Source Graph Drawing Software." Available: http://www.research.att.com/sw/tools/graphviz/ [April 20, 2006].
Banks, D., Carley, K.M. 1996. “Models of Social Network Evolution.” Journal of Mathematical Sociology 21(1-2): 173-196.
Barabasi, A-L. 2002. Linked: The New Science of Networks. Cambridge, MA: Perseus Publishing.
Bar-Yam, Y. 1997. Dynamics of Complex Systems. Perseus Books.
Batagelj, V., Mrvar, A. 2004. Pajek-Program for Analysis and Visualization of Large Networks Reference Manual: List of commands with short explanation. Available: http://vlado.fmf.uni-lj.si/pub/networks/pajek/ [April 20, 2006].
Batagelj, V., Mrvar, A. 1998. “PAJEK: Program for Large Network Analysis.” Connections 21: 47-57.
Blythe, J., McGrath, C., Krackhardt, D. 1995. "The Effect of Graph Layout on Inference from Social Network Data." Symposium on Graph Drawing GD 95. Passau.
Boer, P., Huisman, M., Snijders, T.A.B., Zeggelink, E.P.H. 2003. StOCNET: An Open Software System for the Advanced Statistical Analysis of Social Networks. Version 1.4. Groningen: ProGAMMA / ICS. Available: http://stat.gamma.rug.nl/stocnet/ [April 20, 2006].
Borgatti, S.P. 2002. NetDraw Network Visualization Software.
Borgatti, S.P., Everett, M., Freeman, L. 2002. UCINET 6 for Windows. Harvard: Analytic Technologies. Available: http://www.analytictech.com [April 20, 2006].
Borg, I., Gronen, P. 1997. Modern Multidimensional Scaling. Springer.
Borner, K., Chen, C., and Boyack, K. 2003. “Visualizing Knowledge Domains.” Annual Review of Information Science and Technology 37: 179-255.
Brandenburg, F., Himsolt, M., Rohrer, C. 1995. "An Experimental Comparison of Force-Directed and Randomized Graph Drawing Algorithms.” Proceedings of the Symposium on Graph Drawing, 76-87.
Branke, J. 2001. "Dynamic Graph Drawing" in M. Kaufmann and D. Wagner (eds.): Drawing Graphs, LNCS 2025. Springer-Verlag, 228-246.
Carley, K.M. 1999. “On the Evolution of Social and Organizational Networks” in Steven B. Andrews and David Knoke (eds.): Vol. 16 special issue of Research in the Sociology of Organizations on Networks In and Around Organizations. Greenwhich, CN: JAI Press, Inc. Stamford, CT, 3-30.
Chen, C., Morris, S. 2003. “Visualizing Evolving Networks: Minimum Spanning Trees versus Pathfinder Networks.” IEEE Symposium on Information Visualization, October 19-21, 2003, Seattle, Washington.
Choudhury, T. 2004. Sensing and Modeling Human Networks. Doctoral Dissertation, Massachusetts Institute of Technology, School of Architecture and Planning.
Choudhury, T., Pentland, A. 2004. “Characterizing Social Networks using the Sociometer.” Proceedings of CASOS 2004 NAACSOS Conference. Available: http://www.casos.cs.cmu.edu/events/conferences/2004/2004_proceedings/Choudhury_Tanzeem.pdf [April 20, 2006].
Collins, R. 1981. "On the Microfoundations of Macrosociology." American Journal of Sociology 86: 984-1014.
Davidson, R., Harel, D. 1996. "Drawing Graphs Nicely using Simulated Annealing." ACM Transactions on Graphics (TOG) 15, 4: 301-331.
Di Battista, G., Eades, P. 1994. “Algorithms for Drawing Graphs: An Annotated Bibliography.” Computational Geometry: Theory and Applications 4, 5: 235-282. Available: http://www.graphdrawing.org/literature/gdbiblio.pdf [April 20, 2006].
Di Battista, G., Garg, A., Liotta, G., Parise, A., Tamassia, R., Tassinari, E., Vargiu, F., Vismara, L. 1996. “Drawing Directed Acyclic Graphs: An Experimental Study.” International Journal of Computational Geometry and Applications 10,6 (2000): 623-648.
Dijkstra, E.W. 1959. "A Note on Two Problems in Connection with Graphs." Numerische Math 1: 269-271.
Doreian, P., Stokman, F. 1997. "The Dynamics and Evolution of Social Networks" in Patrick Doreian and Frans Stokman (eds.): Evolution of Social Networks, Gordon and Breach Publishers, 1-17.
Doreian, P., Stokman, F. (eds). 1997. Evolution of Social Networks. Gordon and Breach Publishers.
Dunne, J., Williams, R., Martinez, N. 2002. “Food-web Structure and Network Theory: The Role of Connectance and Size.” Proceedings of the National Academy of Science USA 99: 12917-12922.
Ferligoj, A., Hlebec, V. 1999. "Evaluation of Social Network Measurement Instruments." Social Networks 21: 111-130.
Freeman, L. 1983. "Spheres, Cubes and Boxes: Graph Dimensionality and Network Structure.” Social Networks 5, 2: 139-156.
Freeman, L.C. 2000a. "Visualizing Social Groups" in the Proceedings of the Section on Statistical Graphics at the American Statistical Association. Available: http://moreno.ss.uci.edu/groups.pdf [April 20, 2006].
Freeman, L.C. 2000b. “Visualizing Social Networks.” Journal of Social Structure 1, 1. Available: http://www.cmu.edu/joss/content/articles/volume1/Freeman.html [April 20, 2006].
Freeman, L.C., Webster, C.M., Kirke, D.M. 1998. "Exploring Social Structure Using Dynamic Three-Dimensional Color Images." Social Networks 20: 109-118.
Frick, A., Ludwig, A., Mehldau, H. 1994. "A Fast Adaptive Layout Algorithm for Undirected Graphs.” Proceedings of the DIMACS International Workshop on Graph Drawing, 388-403.
Fruchterman, T., Reingold, E. 1991. "Graph Drawing by Force-directed Placement." Software-Practice and Experience 21,11: 1129-1164.
Furnas, G.W., Bederson, B.B. 1995. “Space-Scale Diagrams: Understanding Multiscale Interfaces.” Proceedings of CHI’95 Human Factors in Computing Systems, Denver, CO.
Gibson, D. 2003. “Participation Shifts: Order and Differentiation in Group Conversation.” Social Forces 81, 4: 1335-1381.
Gibson, J. 1986. The Ecological Approach to Visual Perception. Lawrence Erlbaum.
Harel, D., Koren, Y. 2002. "Graph Drawing by High-Dimensional Embedding." Graph Drawing, 10th International Symposium, Revised Papers, Lecture Notes in Computer Science 2528. Springer.
Himsolt, M. 1995. “Comparing and Evaluating Layout Algorithms within GraphEd.” Journal of Visual Languages and Computing 6.
Hoschek (CERN). 1999. Colt; Open Source Libraries for High Performance Scientific and Technical Computing in Java. Available: http://www-itg.lbl.gov/~hoschek/colt/ [April 20, 2006].
Jin, E.M., Girvan, M., Newman, M.E.J. 2001. “The structure of growing social networks.” Phys. Rev. E 64: 046132.
Johnson, J.C. 2002. “Network Visualization of Social and Ecological Systems.” Paper presented at the Russian-American Workshop on Studies of Socio-Natural Co-Evolution from Different Parts of the World, Academgorodok, Siberia.
Kamada, K., Kawai, S. 1989. "An Algorithm for Drawing General Undirected Graphs." Information Processing Letters 31: 7-15.
Killworth, P.D., Bernard, H.R. 1979. “Informant Accuracy in Social Network Data III: A Comparison of Triadic Structure in Behavioral and Cognitive Data.” Social Networks 2: 10-46.
Killworth, P.D., Bernard, H.R. 1976. “Informant Accuracy in Social Network Data.” Human Organization 35: 269-286.
Krackhardt, D., Blythe, J., McGrath, C. 1994. "KrackPlot 3.0: An Improved Network Drawing Program." Connections 17, 2: 53-55.
Krempel, L., Plümper, T. 2004. “Exploring the Dynamics of International Trade by Combining the Comparative Advantages of Multivariate Statistics and Network Visualization.” Journal of Social Structure 4, 1. Available: http://www.cmu.edu/joss/content/articles/volume4/KrempelPlumper.html and http://www.cmu.edu/joss/content/articles/volume4/KrempelPlumper_files/KrempelPlumper.pdf [April 20, 2006].
Krempel, L. 1999. “Visualizing Networks with Spring Embedders: Two-mode and Valued Data.” American Statistical Association 1999, Proceedings of the Section of Statistical Graphics, Alexandria, VA, 36-45. Available: http://www.mpi-fg-koeln.mpg.de/%7Elk/netvis/baltimore/index.html [April 20, 2006].
Kruskal, J., Wish, M. 1978. Multidimensional Scaling. Sage Publications: Beverly Hills, CA.
Leenders, R. 1997. "Longitudinal Behavior of Network Structure and Actor Attributes: Modeling Interdependence of Contagion and Selection" in Patrick Doreian and Frans Stokman (eds.): Evolution of Social Networks, Gordon and Breach Publishers, 165-184.
Lorrain, F., White, H.C. 1971. "The Structural Equivalence of Individuals in Social Networks." Journal of Mathematical Sociology 1: 49-80.
Luczkovich, J.J., Johnson, J.C. 2004. “Dynamic Visualization of Trophic Role Similarity in Estuarine Food Webs." AERS Annual Meeting, Salisbury, MD.
Marsden, P.V. 1990. "Network Data and Measurement." Annual Review of Sociology 16: 435-463.
McFarland, D.A. 2005. “Why Work When You Can Play? Dynamics of Formal and Informal Organization in Classrooms” Chapter 8 in Larry Hedges and Barbara Schneider (eds.): The Social Organization of Schooling, New York: Russell Sage Foundation, 147-174.
McFarland, D.A. 2004. “Resistance as a Social Drama: A Study of Change-Oriented Encounters.” American Journal of Sociology 109, 6: 1249–1318.
McFarland, D.A. 2001. “Student Resistance: How the Formal and Informal Organization of Classrooms Facilitate Everyday Forms of Student Defiance.” American Journal of Sociology 107, 3: 612-678.
McFarland, D.A., Bender-deMoll, S. 2003. “Classroom Structuration: A Study of Network Stabilization.” Working paper, Stanford University.
McGrath, C., Blythe, J., Krackhardt, D. 1997. "Seeing Groups in Graph Layouts." Available: http://www.andrew.cmu.edu/user/cm3t/groups.html [April 20, 2006].
McGrath, C., Blythe, J. 2004. “Do You See What I Want You to See? The Effects of Motion and Spatial Layout on Viewers' Perceptions of Graph Structure.” Journal of Social Structure 5, 2. Available: http://www.cmu.edu/joss/content/articles/volume5/McGrathBlythe/ [April 20, 2006].
McGrath, C., Blythe, J., Krackhardt, D. 1997. "The Effect of Spatial Arrangement on Judgments and Errors in Interpreting Graphs." Social Networks 19: 223-242.
Monge, P., Contractor, N. 2003. Theories of Communication in Networks. Oxford, UK: Oxford University Press.
Moody, J., McFarland, D.A., Bender-deMoll, S. 2005. “Visualizing Network Dynamics.” American Journal of Sociology 110, 4 (January 2005). Available: http://www.journals.uchicago.edu/AJS/journal/issues/v110n4/080349/080349.web.pdf [April20, 2006].
Moody, J. 2001. “Peer Influence Groups: Identifying Dense Clusters in Large Networks Social Networks 23:261-283.
Morgan, D.L., Neal, M.B., Carder, P. 1995. “The Stability of Core and Peripheral Networks over Time.” Social Networks 17: 273-297
Munzner, T. 1997. “H3: Laying Out Large Directed Graphs in 3D Hyperbolic Space.” Proceedings of the 1997 IEEE Symposium on Information Visualization, October 20-21, 1997, Phoenix, AZ: 2-10.
Newcomb, T.M. 1961. The Acquaintance Process. New York: Holt, Rinehart, Winston.
O'Mahony, S., Ferraro, F. In Press. "Managing the Boundary of an Open Project" in W. Powell and J. Padgett (eds.): Market Emergence and Transformation, MIT Press.
Padgett, J.F., Ansell, C. 1993. “Robust Action and the Rise of the Medici, 1400-1434.” American Journal of Sociology 93, 6: 1259-1319.
Papachristos, A.V. 2004. “Murder as Interaction: A Network Approach to Street Gang Homicide.” Presented at the annual meeting of the American Sociological Association, San Francisco.
Powell, W.W., White, D.R., Koput, K.W., Owen-Smith, J. 2005. "Network Dynamics and Field Evolution: The Growth of Interorganizational Collaboration in the Life Sciences." American Journal of Sociology 110, 4 (January 2005). Available: http://www.journals.uchicago.edu/AJS/journal/issues/v110n4/080171/080171.web.pdf [April 20, 2006].
R Foundation. 2004. R Project for Statistical Computing. Available: http://www.r-project.org/ [April 20, 2006].
Ridgeway, C., Johnson, C. 1990. “What Is the Relationship between Socioemotional Behavior and Status in Task Groups.” American Journal of Sociology 95 (5): 1189-1212.
Robins, G.L., Pattison, P., Wasserman, S. 1999. "Logit Models and Logistic Regressions for Social Networks: III Valued Relations. Psychometrika 64: 371-394.
Rothenberg, R.B., Potterat, J.J., Woodhouse, D.E. et al. 1998. “Social Network Dynamics and HIV Transmission.” AIDS 12: 1529-1536.
Roy, W.G. 1983. "The Unfolding of the Interlocking Directorate Structure of the United States." American Sociological Review: 248-257.
Sanil, A., Banks, D., and Carley, K. 1995. “Models for Evolving Fixed Node Networks: Model Fitting and Model Testing.” Social Networks 17, 1: 65-81.
Scott, J. 2000. Social Network Analysis. Newbury Park, CA: Sage.
Schvaneveldt, R.W., Dearholt, D.W., Durso, F.T. 1988. “Graph Theoretic Foundations of Pathfinder Networks.” Computer Mathematics Applications 15, 4: 337-345.
Snijders, T.A.B., Van Duijn, M.A.J. 1997. "Simulation for Statistical Inference in Dynamic Network Models" in Rosaria Conte, Rainer Hegselmann and Pietro Terna (eds.): Simulating Social Phenomena, New York: Springer, 493-512.
Snijders, T.A.B. 1996. "Stochastic Actor-Oriented Models for Network Change." Journal of Mathematical Sociology 21 (1-2): 149-172.
Snijders, T.A.B. 2001. “The Statistical Evaluation of Social Network Dynamics.” Sociological Methodology: 361-395.
Sugiyama, K., Misue, K. 1995. "A Simple and Unified Method for Drawing Graphs: Magnetic-Spring Algorithm." Lecture Notes in Computer Science 894, Springer Verlag: 364-375.
Tufte, E. 1983. The Visual Display of Quantitative Information. Graphics Press.
Motoyoshi, M., Miura, T., Watanabe, K. 2002. “Data Streams and Time-Series: Mining Temporal Classes from Time Series Data.” Proceedings of the Eleventh International Conference on Information and Knowledge Management.
Wasserman, S., Pattison, P. 1996. "Logit Modles and Logitic Regressions for Social Networks: I. An Introduction to Markov Graphs and P*." Psychometrika 61: 401-425.
Wellman, B., Berkowitz, S.D. (eds.). 1988. Social Structures: A Network Approach. Cambridge: Cambridge University Press.
Yee, K., Fisher, D., Dhamija, R., Hearst, M. 2001. "Animated Exploration of Graphs with Radial Layout." IEEE Symposium on Information Visualization, 43-50.
Footnotes
1. This in an equally co-authored paper (names in alphabetical order). The project was generously supported by a research incentive award given to McFarland by Stanford University's Office of Technology and Licensing (grant #2-CDZ-108). We thank the editor and anonymous JoSS reviewers for their insightful comments, and extend special thanks to Kaisa Snellman, Ben Shaw, Ozgecan Kocak, and James Moody for their contributions at various stages of this project. We also benefited from valuable feedback from participants of James G. March’s “Monday Munch” at Stanford University and participants at the satellite symposium run by Tom Snijders, “Dynamics of Networks and Behavior,” in Portoroz, Slovenia (2004). Please send all correspondence to Daniel A. McFarland, 485 Lasuen Mall, Stanford, CA 94305 (mcfarland@stanford.edu).
2. However, most authors of noncommercial programs are willing to discuss their programs, so the issue is not one of intentional secrecy.
3. We might also consider a third category of "pseudo-networks" or "similarity networks" constructed from sets of entities fully connected by something like a similarity measure or a co-occurrence count from which a network is then extracted for analytical purposes.
4. In fact, occasional conflicts may actually serve to bring friends closer than if they have consistently supportive interchanges. Averaging and intermittent surveys can miss these uncommon central moments in the service of salient ones, thereby missing an important mechanism of relational formation and change.
5. All digital or numerically coded information must be discretized but, by using a lot of decimal places, pretty good approximations to real-valued data can be achieved.
6. In a sense this is a paradox. If we are using discrete time, then the chunks form the fundamental intervals and no finer graduations should be possible. But in network data, the chunks may be large (days or weeks) and we may want to think of the process in more detail than that, essentially dividing it into smaller intervals using a decimal system.
7. However, the links in citation or bibliographic networks are often represented as directed from a later to a previous time. This kind of link may be difficult to represent in this framework.
8. The importance of the flexibility is explained in our discussion of animation below.
9. Because we are intersecting intervals, the rule is fairly complicated. The exact definition of the slice is a "right-open" interval, where events contained within the bounds (or starting within the bounds) are included. Event intervals intersected by the slice are also included, but event intervals that begin before and end within the slice are excluded for symmetry. In other words, we include an event in a slice if: ((eventStart >= sliceStart) AND (eventStart < sliceEnd)) OR ((eventStart <= sliceStart) AND (eventEnd > sliceEnd)).
10. An interesting possibility for thinking about the ties in time-based networks is to consider them as a rate instead of a weight. The difference in weight over an interval of time is analogous to the derivative in calculus. This could lead to a more sophisticated structure for modeling the network and would require data structures more advanced than the slicing technique now used.
11. One of the purposes of creating the SoNIA software is to allow us to easily vary these parameters, without having to conduct multiple surveys.
12. This kind of "2.5-dimensional” projection is conceptually similar to Principal Component visualization. Drawn are two-dimensional composite vectors expressing the most important information from three-dimensional data.
13. In Kruskal's "f-stress" (Kruskal 1978), the MDS and matrix distances are compared for all i and j.
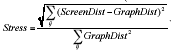 Where screen distance is the Euclidean distance of the layout x - y
coordinates and GraphDist is the geodesic distance. In SoNIA's version, one comparison is made for each
connected node pair, allowing all the components in the layout to be included, but at the cost of slightly
distorting the measure.
Where screen distance is the Euclidean distance of the layout x - y
coordinates and GraphDist is the geodesic distance. In SoNIA's version, one comparison is made for each
connected node pair, allowing all the components in the layout to be included, but at the cost of slightly
distorting the measure.
14. As mentioned earlier, there are many kinds of data under the label of "network." For some variants (planar graphs, acyclic trees, etc.), specialized representations and visualization procedures are possible and may be more effective.
15. Another, perhaps more traditional, approach is to use the adjacency matrix as input for row or column correlations, resulting in a correlation matrix giving nodes' similarities, which can be used as a consistent distance measure after undergoing a dissimilarity transformation. We would argue that while this approach is useful, the result is a plot of node similarities that should not be confused with a plot of distance structure (Lorrain and White 1971).
16. Multiplex ties occur when there is more than one kind of tie linking two nodes.
17. Moody (2001) has worked some with negative values in his peer influence (PI) algorithm.
18. Some users have suggested the intriguing possibility of allowing nodes to be "born" at the location of a parent node.
19. Most layout algorithms do not take into account the positions of the nodes in the "previous" slices?the "rubber band" layout may be an exception (see SoNIA). A "smart" layout might measure the network change from the previous slice and use this as an aid in setting the annealing criteria. Also see the discussion on chaining layouts.
20. Displaying large networks, or networks which change size, can cause problems in maintaining a consistent rate of animation due to the delays caused by rendering lots of data to the screen. This is one reason that SoNIA has the option to export animations to a constant-rate movie format, such as QuickTime.
21. For networks built from discrete events, it may be possible to construct a statistical model of the network process and run it as a simulation to generate in-between events. Such procedures (for small networks) already exist in SIENA (Boer et al. 2003), although the process of model estimation can be computationally expensive. We are collaborating with the authors of SIENA on ways to exchange data with SoNIA.
22. Because the time-window of the render slice can be of any size, it is likely that there will be multiple relations between a pair of nodes, or there may bemore than one active definition for a node attribute during that period. We handle this in SoNIA by simply drawing all of the arcs on top of each other, in no particular order (although the order probably roughly follows the order which they were parsed from the file, so "recent" arcs are usually on top). SoNIA defaults to draw arcs with partial (50%) transparency, making it possible to distinguish situations when multiple arcs have been drawn from single arcs (multiple arcs will appear darker and more saturated), especially if arcs have different colors. This has been a criticism of past network visualization programs. Multiple node events (changes in size, color, etc.) can also be drawn, but usually obscure transparent arcs.
23. All of the render and layout parameters can be entered manually, making it possible to display the events of one time interval with the coordinates of another by entering arbitrary slice numbers and render slice time-coordinates ("display time" and "duration" fields in the layout window). Or, if the underlying data are "streaming" or un-binned event data, very short duration render slices can be used to browse or tease-apart fine scale interactions, inspecting them almost tie-by-tie.
24. SoNIA allows color specification with either color names or numerical RGB values, see http://www.stanford.edu/group/sonia/documentation/inputFormats.html for .son input format.
25. QuickTime is an interchange format for multimedia files developed by Apple Computer, available free on Windows and Mac platforms. http://www.apple.com/quicktime/download/.
26. This has been attempted in several other graph visualization packages. See Himsolt 1995 “GraphEd."
27. The definition of the input file format is available online at http://www.stanford.edu/group/sonia/documentation/inputFormats.html.
28. A reasonable idea for a non-arbitrary starting position is to apply a layout to an aggregation of the entire network and use the resulting coordinates to start each slice.
29. A variety of “set” starting positions are possible, such as a circle starting configuration, a randomly-generated set, the prior slice, or a set defined by the user (e.g., seating chart). When using random numbers, it is possible to regenerate a layout exactly by using the same random number seed and layout parameters. See our discussion of repeatability below.
30. This is a problem for the first slice, and when a new node is added, which makes the choice of starting positions important.
31. We distinguish two kinds of re-centering: “Regular” places the window at the center between max and min of x and y coordinates, and “Barycenter” centers the window on the average of x and y coordinates, so it is less likely to be affected by isolates and more likely to focus on the largest component.
32. The current version of SoNIA gives fairly crude options for scaling and zooming. The overall size of the layout area can be changed, but this does not graphically alter the network; rather, it adjusts the amount of "room" available for positioning a network. It is possible to scale up or down nodes' or arcs' graphic elements by specifying a node or arc scale factor. For some layouts, there is an "optimal distance" parameter that influences the spacing of nodes on the screen (see our discussion of individual algorithms below). It is easy to see that pan and zoom controls for the display would be helpful, especially when dealing with large networks, but a system would be needed for determining what portion of the network would be viewed when animations are exported.
33. No software is ever bug-free, and SoNIA is no exception?we hope that opening the source for inspection and contribution will help with this. Details of bugs and fixes, user forums and email lists, and the complete set of source files for download in compressed archive or by anonymous CVS are located at http://sourceforge.net/cvs/?group_id=119448.
34. The first entry in the log file is the seed for the random number generator. Some of the routines in SoNIA require the use of random numbers. Because it is impossible to have "true" random numbers on contemporary computers, SoNIA makes uses of the "pseudo-random" number generation provided in the Colt package (CERN) of numerical algorithms for Java. The Colt package generally uses the very long period Mersenne Twister algorithm, which is reportedly one of the best available. Normally SoNIA seeds the generator with the clock time, and reports the seed value to the log. When launching SoNIA from the command line it is possible to specify the random number seed so that, if the same sequence of commands is followed, the same layout will result.
35. We thank Ben Shaw for his comments in using such techniques to test layouts, and for having the patience to do it manually!
36. Borg and Groenen (1997) provide an argument for why simply correlating the distances is inappropriate, and also propose a “congruence coefficient” that may be useful here.
37. The threshold distance is necessary to allow for round-off errors and sub-pixel mismatches in the coordinate positions, and to provide a way to vary the strictness of the matching definition.
38. The problem of removing these "non-distorting" transformations before comparing two data-sets is fairly common, and is referred to as "procrustes transformation" in MDS and "image registration" in research areas such as medical imaging and cartography. Hopefully we will be able to mine the literature of these fields for accurate algorithms.
39. Our desire to make the source code to SoNIA freely available stems in part from this problem: In existing software it is difficult to determine what choices were made in implementation.
40. Brandenburg, Himsolt, and Roher (1995) also present a larger experimental comparison of force-directed graph algorithms with timings and example graphs; see also Himsolt (1995).
41. Harel and Yehuda (2002) have demonstrated an elegant projection created by a high dimensional embedding algorithm that seems to be a good proof-of-concept, as well as being extremely fast and almost parameter-free. However, their examples had very low amounts of random connections.
42. The Newton-Raphson optimimization evaluates the system of equations to find the direction and steepness of layout forces at a given point, and then takes repeated “steps” in the most probable direction of the optima.
43. The optimal distance parameter acts as a scale factor, giving the number of pixels per unit of graph distance.
44. It is also interesting to consider that the KK algorithm should work with any symmetric distance measure, not just geodesic distance, making it easily adaptable to other social-space models.
45 The equations in the FR algorithm actually give displacement, not force, making "force-directed layout" something of a misnomer.
46. The parameter values for the curve can be displayed and reentered for repeatability.
47. We experimented briefly with a randomized version of the FR algorithm, which updates the positions of single nodes at random. Results were promising, but more investigation is needed.
48. This coding method was piloted in two prior studies by McFarland (2001), and had a high degree of accuracy in more teacher-centered classroom lessons because of the turn-taking sequential nature of discourse. In more chaotic classrooms, simultaneous turns at talk often prevented the observer from acquiring perfect accuracy. However, some record was made of when such diminished accuracy was acquired. The two class periods used in this paper were considered to have a high degree of accuracy in their coding.
49. This class period’s data is available on the SoNIA website along with the log file so users can replicate, test, critique and improve on the movie (http://www.stanford.edu/group/sonia/examples/McFarlaClass.html). The only parameter we changed from the default settings in SoNIA is a circle starting configuration. After the first slice was graphed, we used the prior graph’s coordinates as the starting configuration for generating the next graph and automated that procedure through the remaining slices.
50. The internal data architecture will need improvement if SoNIA is going to work well with larger networks. It is also likely that many of the techniques we have employed will not scale well with network size, and will need to be adapted and improved.
51. We have recently learned of development by Peter Gloor, Rob Laubacher, Scott Dynes and Yhan Zhao of a program with some similar features and conceptual underpinnings (http://www.ickn.org/ickndemo/).