JoSS Article: Volume 6
Conceptual Distance in Social Network Analysis
Anthony Dekker, Tony.Dekker@dsto.defence.gov.au
Defence Science and Technology Organisation, Australia
Abstract: In this paper we present an approach to Social Network Analysis, based on statistical analysis of conceptual distance between people. In particular, we introduce the concept of valued centrality and a generalisation of geodesic distance which we call link distance. We examine a number of benefits of the link distance concept, including ease of visualisation and applicability of common statistical methods. Using a case study, we demonstrate how examining the statistical relationships between link distance and other forms of conceptual distance can offer insights into the nature of communication within an organisation. Thus an integration of the graph-theoretic techniques traditional in Social Network Analysis, and the statistical techniques traditional in other Social Sciences, leads to a combined technique which integrates the strengths of both approaches.
Contents
- Introduction
- Defining Distance
- Case Study
- Robustness
- Information Propagation
- Other Forms of Distance
- Conclusions
- Acknowledgements
- References
1. Introduction
Social Network Analysis [1] is an approach to studying organisations focusing on analysing the networks of relationships between people and/or groups as the most important aspect. Going back at least to the 1950's, it is characterised by adopting mathematical techniques especially from graph theory [2, 3]. It has applications in organisational psychology, sociology, and anthropology. An excellent overview of the field is given by Wasserman and Faust [1].
Social Network Analysis provides an avenue for analysing and comparing formal and informal information flows in an organisation, as well as comparing information flows with officially defined work processes. We are interested in applying Social Network Analysis to military organisations, and especially to military headquarters ranging from brigade to national strategic levels.
An important aspect of Social Network Analysis is the visualisation of communication and other relationships between people and/or groups, by means of diagrams. Visualisation of Social Networks has a long tradition, and an excellent historical survey is given by Freeman [4]. Visualisation of Social Networks is important because of the complexity of organisational structure, and the need for good visual representations of how an organisation functions.
A second aspect is the study of factors which influence relationships, for example the age, background, and training of the people involved. Studying the correlations between relationships is also important, since it offers insights into the reasons why relationships exists. These studies can be done using traditional statistical techniques such as correlation, analysis of variance, and factor analysis, but also require appropriate visualisation techniques.
The ultimate goal of Social Network Analysis is often to draw out implications of the relational data, in order to make recommendations to improve communication and workflow in an organisation. This is the major motivation for our Social Network Analysis programme. In previous work [5, 6, 7], we have applied Social Network Analysis to military organisations. In the course of this work, we have found conceptual distance to be the most useful construct in explaining relationships. This is partly because the human brain is skilled at thinking about and visually judging distances. In this paper we argue the benefits of using conceptual distance for analysing Social Networks, and demonstrate how to do so using a case study.
2. Defining Distance
We have found valued networks to be the most useful for modelling social and work relationships. In valued networks, each link is assigned a value, which we take to be in the range 0 (non-existent link) to 1 (strongest possible link). This provides a more accurate description of reality than simply regarding links as "present" or "absent." It also avoids a serious problem with non-valued networks, namely the making of arbitrary choices as to how much communication constitutes a link being "present." We also generally use directed networks, with arrows from A to B reflecting A's perception of (and in some cases A's contribution to) the communication between A and B.
There are several ways of obtaining these 0-1 link values. We have generally found it useful for link values to be coded pseudo-logarithmically. A typical example of how we have coded communication in some of our Social Network Analysis studies is:
- 1.0 = communication every day
- 0.8 = two or more times per week
- 0.6 = once per week
- 0.4 = once per two weeks
- 0.2 = once per month
- 0.0 = less than once per month (non-existent link)
This is pseudo-logarithmic in the sense that the codes 0.2 to 1.0 are approximately proportional to the logarithm of n+1, where n is the number of working days per month in which communication occurs. If, on the other hand, we had obtained 0-1 link values by simply scaling the number of communication days per month, we would have obtained a highly skewed distribution. Based on four of our past Social Network Analysis surveys, at least 70% of links would have had a value less than 0.3. Using a pseudo-logarithmic coding also does more justice to the value of weak links, which are known to be sociologically very important [8].
Finally, a pseudo-logarithmic coding suits the recall of communication by most respondents, which is generally more accurate for frequent communication. Taking logarithms converts an erroneous doubling or halving of the communication frequency to an erroneous shift up or down by about 0.2. Using this kind of pseudo-logarithmic coding, the 180-degree correlation between coded responses is typically in the range 0.6 to 0.7, i.e. there is a correlation of 0.6 to 0.7 in the assessments of communication frequency by the two parties involved. This is similar to correlations between answers to related questions in many social science surveys, and we consider a correlation in this range sufficient to validate our Social Network Analysis surveys.
It is also possible to obtain 0-1 link values based on the amount, rather than the frequency, of communication, and we do this in the case study described in Section 3.
There is an obvious way of translating this notion of 0-1 link values into a general concept of link distance between people. This is based on three principles:
- High values reflect closeness, i.e. the distance along a specific link (with value v) will be 1/v. The distance along a link will therefore range from 1 (closest) to infinity (furthest away).
- Symmetry, i.e. we wish the distance from A to B to be the same as the distance from B to A. If there is a link from A to B and also one from B to A, we calculate the distance using the higher of the two values. This is based on the fact that people are more likely to forget communication (giving a value that is too low) than they are to hallucinate communication that did not occur (giving a value that is too high).
- Additivity: we obtain the distance between any two people (even if there is no direct link) by adding distances for all the links in the path between them. If there are multiple paths between people, we define the distance using the shortest path. If there are no paths, we define the distance as infinite.
This definition is essentially the same as that of Flament [9] and generalises the concept of geodesic distance in non-valued networks. The criticism of this definition by Yang and Knoke [10] reflects a misunderstanding of the relationship between value and distance, and the fact that high values correspond to short distances. However, there is some merit in their suggestion that distances should reflect the number of links in the path between two people as well as the values of the links. By using our pseudo-logarithmic coding of value, we actually obtain the desired bias towards paths with few links, and we do so using the obvious definition of distance, without the complex and inelegant distance definition of Yang and Knoke [10].
This definition of link distance has a number of advantages, which we discuss in detail in the body of the paper:
- Efficiency: this definition of distance can be computed efficiently, using the algorithms of Floyd, Dijkstra, or Johnson [11]. Johnson's algorithm is significantly more efficient for very large social networks. We have constructed a Java-based tool suite called CAVALIER (Communication and Activity VisuALIsation for the EnteRprise), to carry out analysis and visualisation of Social Networks, and that tool incorporates link distance calculation (all the diagrams in this paper have also been produced using the CAVALIER tool).
- Visualisation: one of the most common techniques for visualising Social Networks is spring-embedding [4]. A spring-embedding layout algorithm assumes that links between nodes behave physically like springs, with an ideal spring length (that corresponds to some kind of conceptual distance between the nodes), and a spring strength (best results are obtained when spring strength decreases as the ideal spring length increases, and this option turns out to be equivalent to Multi-Dimensional Scaling [12]). The nodes can be assigned to points in two-dimensional or three-dimensional space by moving them in a way which minimises the total stress in the entire collection of strings, using straightforward physics. Link distance is easily visualised, because it correlates well with physical distance after a spring-embedding layout algorithm is used. Figure 1 and Figure 2 provide examples of this.
- Robustness: link distances do not change radically if some people fail to complete survey forms (a serious problem when survey participation is voluntary). Section 4 discusses this issue in more detail.
- Correlation with propagation time: in simulation experiments, link distance correlates well with the time to propagate information through the network from the most central node. Typical correlations are in the range 0.8 to 0.9. Section 5 discusses a number of such simulation experiments in detail.
- Normality: link distances are approximately normally distributed, with low values of skew and kurtosis. The vertical axis of Figure 10 indicates this visually, and the case study illustrated there had a skew of 0.35 and a kurtosis of -0.14 for link distance. Section 3 describes this case study (based on Internet newsgroups) in more detail. For comparison, Table 1 summarises the values of skew and kurtosis for other Social Network Analyses studies that we have conducted. Values in the range -1 to +1 are considered approximately normal, and since the actual range of values for skew and kurtosis is well within these limits, link distances are approximately normally distributed in each case.
The reason for the approximate normal distribution of link distances lies in the fact that weak links, though generally more common than strong links, are less likely to occur on the shortest paths (geodesics) between nodes, and that therefore the different possible link values are approximately equally likely to occur on any given geodesic. An analysis of the networks listed in Table 1 confirms that this is, in fact, the case. Applying the definition of link distance to the multiple links in a geodesic produces an approximately normal distribution because of the Central Limit Theorem [13], in much the same way that the sum of multiple Likert scales [14] produces an approximately normal distribution.
| Type of Network | Network Size | Skew | Kurtosis |
| Work communication (scientific) | 20 | 0.03 | -0.71 |
| Work communication (military) | 47 | 0.15 | -0.61 |
| Work communication (scientific) | 63 | 0.00 | -0.72 |
| Work communication (scientific) | 93 | 0.09 | -0.06 |
| Internet newsgroup (Section 3) | 343 | 0.35 | -0.14 |
Table 1: Values of Skew and Kurtosis for Link Distance for Some Social Networks
Normality is extremely important, because it means that the standard toolkit of statistical techniques can be used to analyse link distance. In our work, we investigate Social Networks by applying such standard statistical techniques as Regression Analysis, Analysis of Variance, and Principal Components Analysis to link distance.
However, link distance is not the only form of conceptual distance useful for Social Network Analysis. Other forms of conceptual distance can be defined, based on similarity of activities, difference in culture, and other factors. Great insight into communication patterns can be achieved by statistically examining the relationship between link distance and other forms of conceptual distance. Section 6 discusses this issue in more detail, and provides some examples taken from other Social Network Analysis case studies [5, 6].
3. Case Study
We have been applying Social Network Analysis to various military headquarters [5, 6, 7]. Confidentiality requirements prevent us from outlining the results of these studies in detail, but in this section we present a case study which uses precisely the same method of analysis, and provides an avenue for detailed discussions of our techniques. Indeed, the case study was chosen to demonstrate both the advantages of these techniques, and how various difficulties are overcome in practice.
This case study was based on samples of postings to the Internet newsgroups soc.religion.christian and soc.religion.islam during January to April 2002. The sampled articles were posted by 343 different people. Whenever person A responded to a posting by person B, this was treated as a (directed) link from A to B.
The value of the (directed) link from A to B was taken to be the logarithm of the total number of words written by person A in response to postings by person B, scaled to be in the range 0-1. This provides a slightly different kind of pseudo-logarithmic coding to that discussed in Section 2, but the same advantages apply. The software we use for processing news articles ignores any quoted articles, and counts only words written by the posting author.
Table 2 shows the top-level country domain for the 343 subjects (the "us" code refers to ".com," ".net," etc. which are US-based, but disguise the country of origin). The differences in Table 2 are not significant under the chi-squared test (p = 0.99, or p = 0.49 when the "us" code is excluded). In other words, the subjects are spread fairly randomly over the planet.
| soc.religion.islam | soc.religion.christian | both | |
| ae | 1 | 0 | 0 |
| au | 5 | 0 | 0 |
| ca | 2 | 2 | 0 |
| cy | 0 | 1 | 0 |
| de | 1 | 2 | 0 |
| is | 1 | 0 | 0 |
| it | 0 | 1 | 0 |
| my | 2 | 0 | 0 |
| nl | 0 | 1 | 0 |
| no | 1 | 0 | 0 |
| nz | 1 | 1 | 0 |
| pk | 1 | 0 | 0 |
| pl | 1 | 0 | 0 |
| sa | 1 | 0 | 0 |
| se | 3 | 1 | 0 |
| sg | 1 | 0 | 0 |
| uk | 11 | 4 | 0 |
| us | 211 | 81 | 6 |
Table 2: Country Domains for News Groups
3.1. Link Distance
Our concept of link value produces a measure of link distance as described in Section 2. In Figure 1, link distance is visualised as a two-dimensional diagram using spring-embedding (as discussed in Section 2). In this diagram, people posting to the soc.religion.christian newsgroup are shown as red boxes, people posting to the soc.religion.islam newsgroup are shown as green circles, and people posting to both newsgroups are shown as amber rounded boxes. The people posting to both newsgroups (they were 6 of them) act as bridges between the two communities. People are identified by index numbers rather than name for confidentiality reasons.
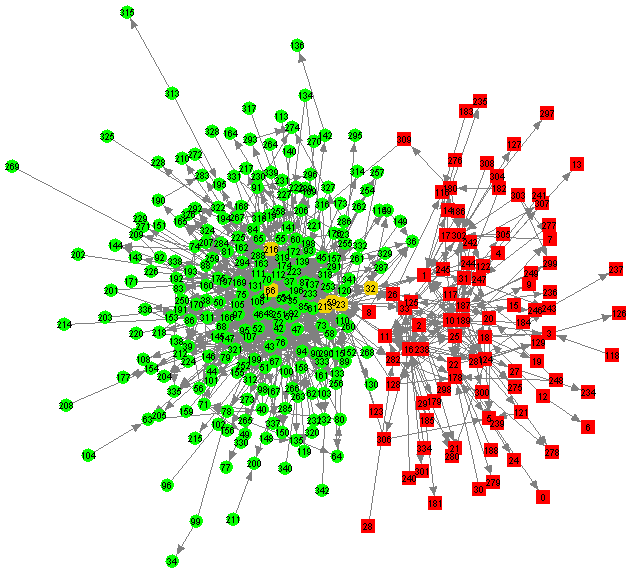 |
Figure 1: Spring-Embedding Layout for Case Study
Such diagrams are generally successful in visualising link distance. In this case, physical distance in the diagram has a 0.82 correlation with link distance (r-squared = 0.67). This correlation value is similar to that obtained in our other studies.
Link distance is often visualised more successfully in three dimensions. Figure 2 shows a three-dimensional spring-embedding layout. For clarity, links are not shown in this diagram. The correlation between physical distance and link distance has been increased to 0.87 (r-squared = 0.76). This value is also similar to that obtained in our other studies.
Figure 2 was obtained using a link from the CAVALIER tool to the Persistence of Vision (POV-Ray) Raytracer (http://www.povray.org/). However, the improved correlation between link distance and physical distance for three-dimensional spring-embedding is only useful if the three dimensions can be directly experienced using motion or stereo. A two-dimensional representation of three dimensions is not sufficient, and many of our clients have reported difficulty in interpreting two-dimensional representations of three dimensions.
Clicking on Figure 2 gives an animated GIF image (produced by exporting from POV-Ray to the Animagic shareware GIF Animator). We have found such animated GIFs useful, because their motion provides a much better understanding of three-dimensional structure, and they can also be easily incorporated in Web pages and PowerPoint presentations. With expert users, we have also had success in visualising Social Networks using Virtual Reality Modelling Language or VRML (http://www.web3d.org/x3d/specifications/vrml/). This technology allows not only animation, but also the ability to manipulate the three-dimensional model interactively. VRML also allows easy linking of explanatory text to nodes.
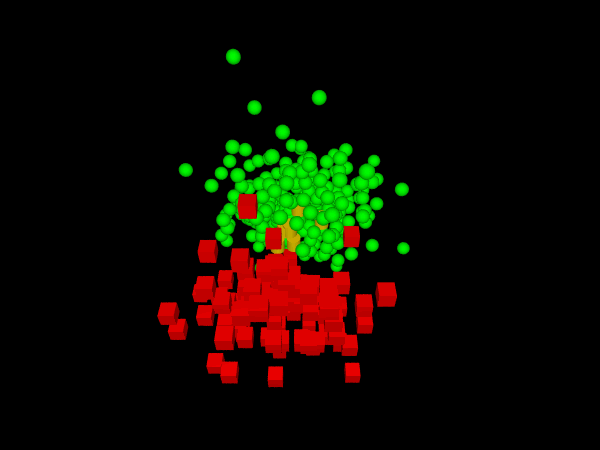
Figure 2: Three-Dimensional Spring-Embedding Layout (click for GIF animation)
Table 3 shows average link distances within and between the three groups of people (the overall average link distance between people is 23.1).
| soc.religion.islam | soc.religion.christian | both | |
| soc.religion.islam | 19.2 | 29.1 | 15.1 |
| soc.religion.christian | 29.1 | 21.2 | 20.9 |
| both | 15.1 | 20.9 | 9.5 |
Table 3: Average Link Distances Within and Between Groups
The differences in Table 3 are statistically extremely significant (p < 0.000001). This is because paths between people posting only to soc.religion.islam and people posting only to soc.religion.christian must contain at least two links, passing through one of the 6 "bridge" people. Also note that (on average) people in the soc.religion.islam and soc.religion.christian groups are closer to the "bridge" people than they are to other group members (this is equivalent to saying that the "bridge" people are highly central). Both these phenomena are visible in Figure 1 and Figure 2.
3.2. Vocabulary Distance
Link distance is not the only form of conceptual distance we can define for this case study. For each person we examined the text that they posted, and recorded the histogram of word frequencies. These histograms are essentially vectors of numbers, and so we can calculate Euclidean distance between these vectors. We call these distances vocabulary distance.
Table 4 shows average vocabulary distances within and between the three groups of people (the overall average vocabulary distance between people is 0.119).
| soc.religion.islam | soc.religion.christian | both | |
| soc.religion.islam | 0.122 | 0.119 | 0.088 |
| soc.religion.christian | 0.119 | 0.113 | 0.083 |
| both | 0.088 | 0.083 | 0.044 |
Table 4: Average Vocabulary Distances Within and Between Groups
It can be seen from Table 4 that vocabulary distances do not differentiate greatly between the newsgroups soc.religion.islam and soc.religion.christian: although differences are significant (p < 0.000001), they are small. This is because topics discussed on both newsgroups are very similar, and because the vocabulary is influenced mostly by the fact that all participants are using the same language. Both newsgroups contain lengthy discussions of the relationships between Christianity, Islam, and Western culture. Figure 3 illustrates this similarity of topic by highlighting in dark blue people (in both groups) who mentioned the Koran (more correctly spelled "Quran") in postings. Similarly, Figure 4 shows people who mentioned the names "Jesus" or "Christ," and Figure 5 shows people who mentioned the words "war" or "peace" (a common topic of discussion for both groups in recent times).
 |
Figure 3: People Mentioning "Koran" or "Quran" in Postings
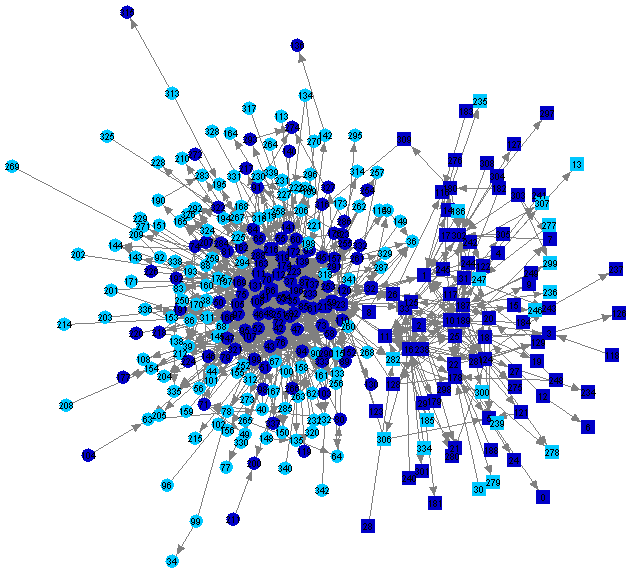 |
Figure 4: People Mentioning "Jesus" or "Christ" in Postings
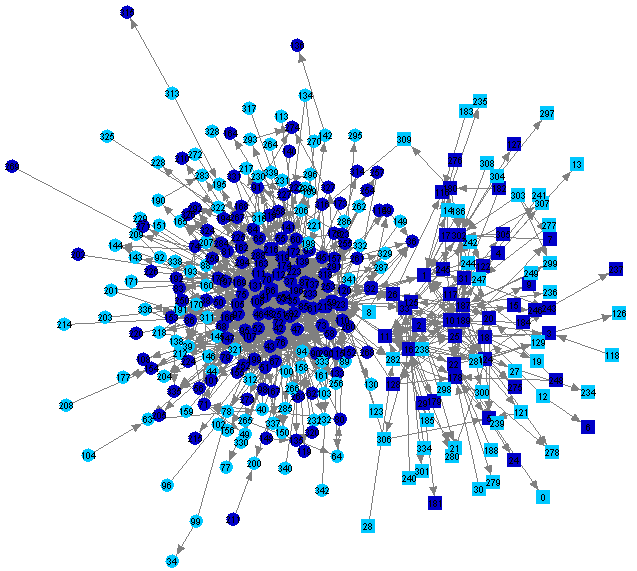 |
Figure 5: People Mentioning "War" or "Peace" in Postings
Table 5 shows the percentage of people in each group mentioning each word. While these differences are statistically significant under the chi-squared test (p < 0.000001, p < 0.000001, and p = 0.025 respectively), there is clearly substantial overlap in topics discussed between groups.
| soc.religion.islam | soc.religion.christian | both | |
| "Koran" or "Quran" | 45% | 5% | 67% |
| "Jesus" or "Christ" | 44% | 81% | 100% |
| "War" or "Peace" | 59% | 49% | 100% |
Table 5: Percentage of People Mentioning Selected Words in Postings
In this example, vocabulary distance has been an instance of the more general concept of a distance measure measuring similarity of activities. For our military headquarters studies, we would obtain a measure of activity-similarity distance by studying work practices and/or administering surveys (Section 6 discusses one such example of activity-similarity distance).
Our case study has shown a particular pattern of communication: a gathering of people engaged in essentially the same activity (discussions of the relationships between Christianity, Islam, and Western culture), but partitioned into two poorly communicating groups. If we saw this pattern of communication within a client organisation, we would consider it as indicating that some kind of management intervention could be required.
3.3. Valued Centrality
Centrality is a critically important concept in Social Network Analysis, and we will see later that it sheds considerable light upon the data. Several different definitions of centrality are possible [1], but the definition we choose for valued graphs, which we call valued centrality, is:
where N is the number of people, distance(A, B) is the link distance between persons A and B (as defined in Section 2), and the sum is carried out over all people except A (note that in the case that A and B are only one step apart, it is simply the value of the link between them that is being added to the sum). This definition of valued centrality is built into our CAVALIER network analysis tool.
This definition essentially takes "closeness" to be the inverse of distance, and obtains valued centrality by averaging closeness values. We feel that this is superior to the definition of "closeness centrality" [1], which is based on adding distances. Closeness centrality is therefore very sensitive to a single large distance or missing link. In the extreme case, disconnecting one node sets distance to infinity and hence closeness centrality of all nodes to 0 (this problem is noted in [1], but no solution is given there). Our definition of valued centrality, on the other hand, is only slightly affected by disconnecting a node. We therefore feel that this stability makes it a more useful definition. The utility of valued centrality in the analysis which follows provides a more pragmatic justification for using it. In particular, valued centrality scores tend to be approximately normally distributed, with low values of skew and kurtosis. The vertical axis of Figure 8 illustrates this visually. Table 6 summarises the values of skew and kurtosis for valued centrality and its inverse for Social Network Analysis studies that we have conducted (the usefulness of the inverse of valued centrality is discussed below). Values in the range -1 to +1 are considered approximately normal, so valued centrality was approximately normally distributed in each case but one. The inverse of valued centrality was also approximately normally distributed in each case but one. The exceptions, which had abnormally high kurtosis, were studies based on survey forms, where the percentage of forms returned was very low. However, even in these cases, an approximately normal distribution could be obtained by choosing to analyse either valued centrality or its inverse.
| Type of Network | Network Size | Return Rate | Skew (Centrality) | Kurtosis (Centrality) | Skew (Inverse) | Kurtosis (Inverse) |
| Work communication (scientific) | 20 | 90% | 0.87 | 0.85 | 0.02 | -0.18 |
| Work communication (military) | 47 | 100% | 0.30 | -0.74 | 0.53 | -0.36 |
| Work communication (scientific) | 63 | 52% | 0.87 | 1.73 | 0.19 | -0.38 |
| Work communication (scientific) | 93 | 52% | 0.43 | 0.25 | 0.72 | 1.25 |
| Internet newsgroup | 343 | 74% | 0.73 | 0.50 | 0.56 | 0.26 |
Table 6: Values of Skew and Kurtosis for Valued Centrality and its Inverse for Some Social Networks
"Betweenness centrality" [1] is also a commonly used centrality measure, and recent work by Brandes [15] shows that it can be computed efficiently. However, "betweenness centrality" requires counting the number of different shortest paths (geodesics) between pairs of nodes. For valued networks this is still possible [15], but in practice valued networks have very few geodesics between pairs of nodes. With our pseudo-logarithmic codings, there is usually (at least 80% of the time) only a single geodesic between any given pair of nodes, as indicated in Table 7. For comparison, Table 7 also shows the number of geodesics for non-valued versions of the networks, where the average number of geodesics between any given pair of nodes ranges from 2.65 to 5.13.
| Type of Network | Network Size | No. of Geodesics (valued) | % Single Geodesic (valued) | No. of Geodesics (non-valued) | % Single Geodesic (non-valued) |
| Work communication (scientific) | 20 | 1-2 (average 1.10) | 90% | 1-11 (average 2.65) | 67% |
| Work communication (military) | 47 | 1-9 (average 1.22) | 84% | 1-68 (average 4.38) | 39% |
| Work communication (scientific) | 63 | 1-5 (average 1.24) | 80% | 1-79 (average 4.23) | 34% |
| Work communication (scientific) | 93 | 1-6 (average 1.24) | 82% | 1-21 (average 3.44) | 32% |
| Internet newsgroup | 343 | 1 | 100% | 1-264 (average 5.13) | 35% |
Table 7: Number of Shortest Paths (Geodesics) for Some Valued and Non-Valued Social Networks
In addition, geodesics in valued networks are very sensitive to changes in link value: changing the value of a single link alters which paths are geodesics. The limited number of geodesics, and their sensitivity to changes in link value, makes "betweenness centrality" a less useful concept for valued networks than it is for traditional non-valued social networks. In the remainder of the paper, we use the term "centrality" to mean valued centrality.
Figure 6 shows a version of Figure 1 coloured using (valued) centrality scores, with red indicating the lowest centrality, yellow a higher centrality, and green the highest centrality. Figure 6 is also drawn without arrowheads, in order to show the structure of the network more clearly. It can be seen that the spring-embedding algorithm places central people close to the centre of the diagram, and that the most central individuals are within the soc.religion.islam group.
 |
Figure 6: Centrality Scores for Case Study
The natural question to ask is: what are the statistical predictors of centrality? What factors determine the centrality of people within this case study?
Table 8 shows centrality scores for the country domains from Table 2. The average centrality value is 0.050, with a standard deviation of 0.012. Analysis of variance shows that the differences in Table 8 are not significant (p = 0.66), i.e. country of origin does not affect centrality. This is typical of the Internet as a whole: physical location in the world is not important. We must therefore turn to other possible predictors of centrality.
| Number of People | Centrality | Standard Deviation | |
| ae | 1 | 0.049 | |
| au | 5 | 0.052 | 0.009 |
| ca | 4 | 0.056 | 0.010 |
| cy | 1 | 0.031 | |
| de | 3 | 0.044 | 0.012 |
| is | 1 | 0.055 | |
| it | 1 | 0.041 | |
| my | 2 | 0.068 | 0.002 |
| nl | 1 | 0.038 | |
| no | 1 | 0.042 | |
| nz | 2 | 0.064 | 0.002 |
| pk | 1 | 0.053 | |
| pl | 1 | 0.055 | |
| sa | 1 | 0.054 | |
| se | 4 | 0.052 | 0.015 |
| sg | 1 | 0.047 | |
| uk | 15 | 0.052 | 0.013 |
| us | 298 | 0.050 | 0.012 |
Table 8: Centrality Scores for Country Domains
Table 9 shows centrality scores for the three groups. Analysis of variance shows that the differences in Table 9 are highly significant (p < 0.000001). The 6 "bridge" people are most central, because of their link to both groups. The soc.religion.islam group is also somewhat more central than soc.religion.christian, because it is larger (given the between-group distances in Table 3, members of a large group generally have more people to whom they are close, and this contributes to a higher centrality score).
| Number of People | Centrality | Standard Deviation | |
| soc.religion.islam | 243 | 0.053 | 0.012 |
| soc.religion.christian | 94 | 0.041 | 0.008 |
| both | 6 | 0.070 | 0.008 |
Table 9: Centrality Scores for Groups
Centrality in Social Networks can often be predicted by numeric attributes of the participants. For each person in this case study we can calculate two parameters: the total number of words posted, and the number of distinct words posted. Both these variables correlate with centrality, but because they are not normally distributed, it is necessary to take logarithms. The logarithm of the total number of words posted predicts 38% of the variance in centrality, while the logarithm of the number of distinct words posted predicts 37% of the variance in centrality. This suggests that we should use the logarithm of the total number of words posted as a predictor of centrality.
However, before we make a decision as to which of these variables is best able to predict centrality, it is important to examine the relationship between them. When we examine the relationship between the two logarithms, we find an extremely high correlation (r = 0.995, r-squared = 0.99). Figure 7 illustrates this relationship. The horizontal and vertical green lines in Figure 7 indicate the mean value and one standard deviation to either side, while the regression line is shown in red.
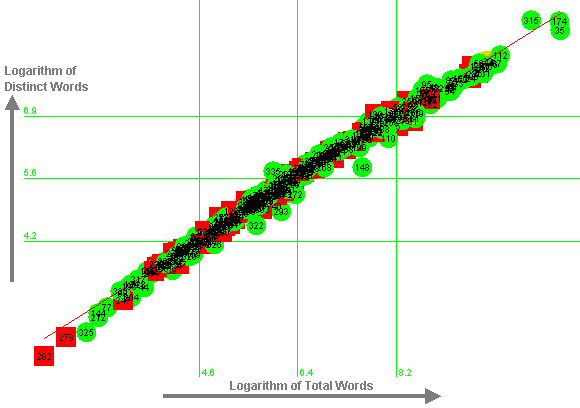 |
Figure 7: Logarithm of Total Words Posted against Logarithm of Distinct Words Posted
This relationship suggests a strong causal dependency between variables, and indeed (since there are no substantial differences in vocabulary between people in this case study), the number of distinct words is simply a consequence of using more new words as the total number of words increases. It therefore makes sense to use the logarithm of the total number of words posted as a predictor of centrality.
We have worked through the statistical analysis of word count in some detail, not because it is an important aspect of our approach to Social Network Analysis per se, but because it provides an example of the kind of statistical analysis that is necessary. In general, a degree of statistical detective work is required to elucidate the relationships between attributes of people, and so to find the best statistical predictors of centrality. In our military studies, rank (considered as a numeric variable) tends to predict between 20% and 40% of the variance in centrality, since generals are usually more central than lieutenants. For some of the informal social networks we have studied, a measure of extraversion [16] also acts as a predictor of centrality, since people with an extravert personality often (though not always) communicate more.
We can improve the prediction of centrality by including the group averages from Table 9, obtaining the regression equation:
This regression equation predicts 58% of the variance in centrality (a correlation of 0.76), as shown in Figure 8.
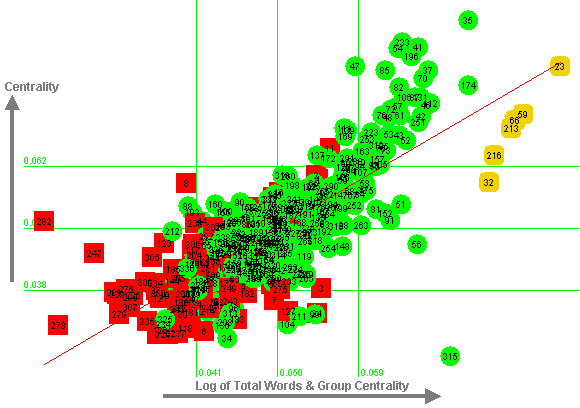 |
Figure 8: Regression Equation against Centrality
The vertical axis of Figure 8 indicates visually that centrality scores are approximately normally distributed. The distribution of points about the mean is approximately symmetrical, and the majority of points are within one standard deviation of the mean. The values of skew and kurtosis are also low (0.73 and 0.50 respectively). Figure 8 also shows the relatively high centrality scores for the 6 "bridge" people (indicated by rounded amber boxes).
3.4. Predicting Distance
We can now turn our attention to predicting the link distance between two people. A statistical predictor for link distance forms the basis for understanding communication patterns within an organisation, and for any intervention that may be required. Factors which increase the link distance between people represent possible obstacles to communication, which management intervention may be able to overcome. We also have a strong interest in the design and refitting of buildings and offices, and an understanding of the factors controlling link distance enables us to place together in a building those people who are "close" in terms of communication.
Vocabulary distance (discussed above) only predicts 8% of the variance in link distance. Normally, a distance measure based on similarity of activity would be a good predictor of link distance. In our previous studies, such an activity distance measure has been able to predict up to 50% of the variance in link distance. However in this case, as we have seen, the people involved in our case study are engaged in essentially the same activity, which makes vocabulary distance less useful.
The best predictor of the link distance between A and B in this case study is in fact the sum of inverse centralities (SOIC):
This predicts 70% of the variance in link distance (a correlation of 0.84). Organisations where link distance depends solely (or almost solely) on centrality are "star-shaped" organisations, with a single central core. Such organisations include flat hierarchies, or organisations controlled by a single influential clique. A "star-shaped" structure can often be cause for concern, since for most organisations there is great value in a sideways flow of information between members. Figure 9 shows how the prediction of link distance by the sum of inverse centralities ranges from 0% for a ring network to 100% for a star network, with grid and tree structures intermediate at 20% and 38% respectively. Table 10 compares the prediction of link distance by centrality for this study with four Social Network Analyses which we have conducted. In those studies, centrality predicted between 40% and 50% of the variance in link distance - a slightly higher percentage than for the tree in Figure 9. Note that the sum of inverse centralities (SOIC) was approximately normally distributed, even for the cases where the centrality alone (or the inverse centrality alone) was not approximately normally distributed. This justifies its use in regression analysis.
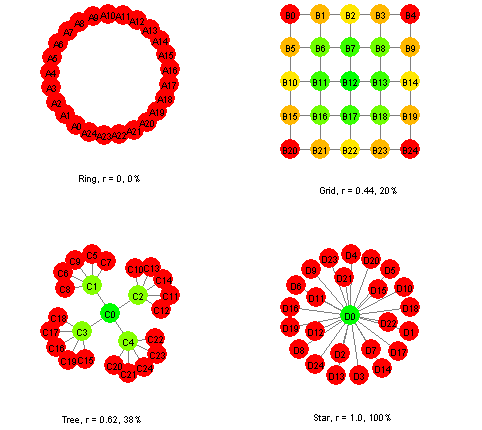 |
Figure 9: Variance in Link Distance Predicted by Centrality for Some Simple Networks
| Type of Network | Network Size | Skew (SOIC) | Kurtosis (SOIC) | Variance Predicted by SOIC | Variance Predicted by Other Factors | Total Variance Predicted |
| Work communication (scientific) | 20 | 0.01 | -0.31 | 40% | 19% | 59% |
| Work communication (military) | 47 | 0.35 | -0.26 | 50% | 33% | 83% |
| Work communication (scientific) | 63 | 0.13 | -0.25 | 43% | 33% | 76% |
| Work communication (scientific) | 93 | 0.49 | 0.50 | 47% | 21% | 68% |
| Internet newsgroup | 343 | 0.39 | 0.11 | 70% | 11% | 81% |
Table 10: Variance in Link Distance Predicted by Centrality for Some Social Networks
The high correlation between link distance and the sum of inverse centralities allows us to approximately predict 58,653 distance scores using only 343 centrality scores, which is a considerable simplification. We should emphasise that the "star-shaped" nature of the network is not necessarily to our analysis, since even for very non-star-shaped social networks a significant fraction of the variance in link distance can still be predicted by the sum of inverse centralities. However, for non-star-shaped social networks, link distance is also very dependent on other factors, such as group structure, physical location, cultural differences, etc.
We can improve the prediction of link distance by including the group averages from Table 3, obtaining the regression equation:
This regression equation predicts an additional 11% of the variance in centrality (a total of 81%, i.e. a correlation of 0.90). Figure 10 illustrates this. The vertical axis of Figure 10 also indicates visually that link distances are approximately normally distributed. The distribution of points about the mean is approximately symmetrical, and the majority of points are within one standard deviation of the mean. The values of skew and kurtosis are also low (0.35 and -0.14 respectively), as discussed in Section 2.
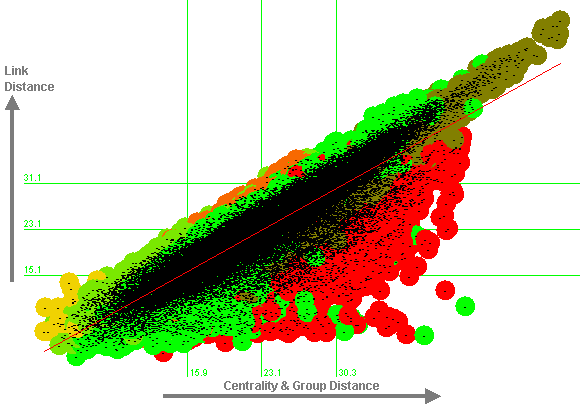 |
Figure 10: Regression Equation against Link Distance
In Figure 10, within-group distances are shown in the appropriate group colour, while between-group distances are shown in yellow-green (for both to soc.religion.islam), orange (for both to soc.religion.christian), and brown (for soc.religion.islam to soc.religion.christian). However, towards the centre of the graph, these colours are obscured by the dashes used as labels (since there are 58,653 data points).
Figure 11 summarises our regression model for predicting distance. Green boxes show variables which are properties of individual people, while blue boxes show variables which are properties of pairs of people.
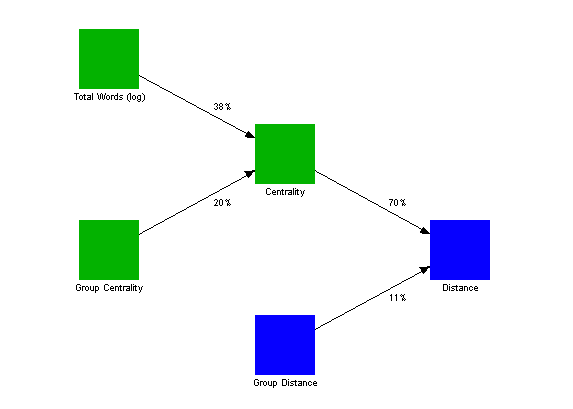 |
Figure 11: Statistical Model for Predicting Link Distance for Case Study
Five conclusions can be drawn from the regression model:
- Communication between people is greatest when one or both parties are central.
- The pair of newsgroups studied is a highly "star-shaped" organisation.
- There is a significant group effect on communication, as described in Table 3 and shown visually in Figure 1 and Figure 2.
- The more text people post, the more central they are likely to be.
- There is also a significant group effect for centrality, as described in Table 9.
Thus a good regression model for link distance forms the basis for an understanding of communication patterns. It can help answer questions such as: Is the group structure impeding communication? Does an organisation suffer from being split over several physical locations? Is there evidence that minority groups are excluded from organisational activities? These answers in turn can form a basis for management intervention. A good regression model for link distance can also assist in adapting building design to suit communication patterns within a particular organisation.
4. Robustness
One practical difficulty with Social Network Analysis is the fact that it is difficult to obtain data for every individual in a group. People are not always available for interview, and survey forms are often not completed. In this section, we investigate the impact of this kind of missing data on link distance.
The experiments reported in this section use data from four Social Network Analysis studies (including the case study in Section 3). However, we first delete all isolated nodes and all nodes with zero out-degree. This is equivalent to selecting a central core of each network for which 100% complete data is available. Naturally, link distance within these central cores is different from the organisation as a whole, but that does not affect the goal of this section, which is to understand the impact of missing data. Table 11 summarises the four networks used.
| Type of Network | Size of Central Core | Number of Missing-Data Nodes | |
| Network C (blue) | Work communication (military) | 18 | 0 to 13 |
| Network J (green) | Work communication (scientific) | 18 | 0 to 13 |
| Network M (red) | Work communication (scientific) | 33 | 0 to 23 |
| Network N (pink) | Internet newsgroup (Section 3) | 168 | 0 to 40 |
Table 11: Networks Used for Missing Data Study
For this experiment, we randomly select between 0 and 40 nodes, and delete all outgoing links from those nodes (simulating the effect of missing survey forms). For a given number of selected nodes, we do this 1000 times. Each time, we calculate link distances between people before and after the deletion of links. As a measure of how badly the deleted links affect the values of link distance, we take the average correlation between the before-deletion link distances and the after-deletion link distances (averaged over all 1000 runs).
The vertical axis of Figure 12 shows the results. As outgoing links are randomly deleted, the average correlation between the before-deletion link distances and the after-deletion link distances drops. This correlation (which we call the average distance correlation for simplicity) measures the impact of missing data. It thus provides an estimate of the correlation between the link distances one obtains in a survey with missing data, and the link distances one would have obtained if only one had been able to get 100% complete data.
Experimentation with different possible regression equations results in the following regression equation, which predicts 97% of the variance in average distance correlation (r = 0.98):
where frac is the fraction of missing-data nodes, n is the size of the network used, and the logarithm of n is cubed.
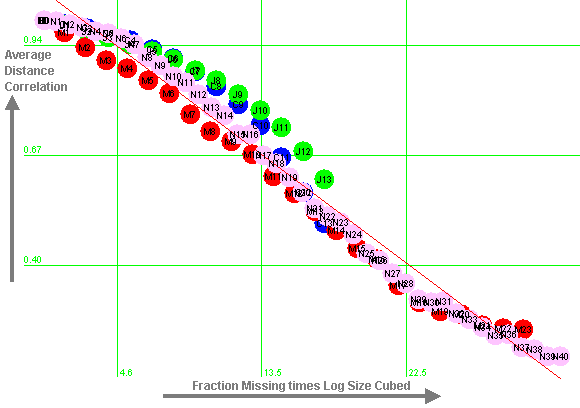 |
Figure 12: Fraction Missing times Log Size Cubed against Average Distance Correlation
Figure 12 illustrates the regression equation graphically, and Table 12 shows the predicted average distance correlation for various network sizes and percentages of missing data. As a consequence of these results, we use a rule of thumb recommending 75% of data as a minimum for small networks (up to 20 people), 90% for medium-sized networks (up to 60 people), and 95% for larger networks.
| n = 20 | n = 40 | n = 60 | n = 80 | n = 100 | n = 150 | n = 200 | |
| 5% | 0.99 | 0.99 | 0.97 | 0.95 | 0.93 | 0.88 | 0.85 |
| 10% | 0.99 | 0.92 | 0.87 | 0.82 | 0.78 | 0.70 | 0.63 |
| 15% | 0.95 | 0.85 | 0.77 | 0.70 | 0.64 | 0.51 | 0.41 |
| 20% | 0.91 | 0.77 | 0.66 | 0.57 | 0.49 | 0.32 | 0.19 |
| 25% | 0.87 | 0.70 | 0.56 | 0.44 | 0.34 | 0.13 | 0.00 |
| 30% | 0.83 | 0.62 | 0.46 | 0.32 | 0.20 | 0.00 | 0.00 |
| 35% | 0.79 | 0.55 | 0.36 | 0.19 | 0.05 | 0.00 | 0.00 |
| 40% | 0.75 | 0.47 | 0.25 | 0.07 | 0.00 | 0.00 | 0.00 |
Table 12: Estimated Average Distance Correlation given Network Size and Missing-Data Percentage
One major cause of these results is that, as the network size increases, the chance that random deletions will isolate some of the most central individuals also increases, which seriously distorts the link distances. The 75%-90%-95% rule of thumb can therefore be relaxed slightly, if we ensure that we have data for the individuals likely to be most central, such as managers and liaison personnel.
If we cannot achieve the 75%-90%-95% rule of thumb, our proposed style of Social Network Analysis is still useful, but we will not be able to draw meaningful conclusions about individual people. For example, we will probably not be able to recognise highly central junior staff who perform an unofficial liaison role. However, we will still be able to draw meaningful conclusions about subgroups within the organisation (as we did in the case study in Section 3), although even restricting our conclusions to subgroups will not be meaningful if the missing data is concentrated in some subgroups and not others.
5. Information Propagation
The simulation experiments reported in this section provide an additional indication of the usefulness of the link distance concept. These experiments studied the speed of propagating a key item of information from the most central node in a network to the other nodes.
We assume that at any given instant in time, the chance of propagating the item of information is random with probability proportional to the link value (we take the probability to be 0.1 times the link value). Since the value is typically pseudo-logarithmically coded, this requires some explanation. The use of pseudo-logarithmic coding has the effect of increasing the propagation probability for occasional contact (e.g. only monthly). However, this is realistic, because such occasional contacts are likely to be scheduled precisely when a key item of information needs to be transferred. In future work, we intend to conduct experimental studies to investigate the precise relationship between propagation probability and link value.
The experiments reported in this section use data from four Social Network Analysis studies. Table 13 summarises the four networks used. We conducted 1000 random (Monte Carlo) simulations for networks C, J, and M, and 100 for network N (the network in Section 3). We examine the average propagation delay (the time to propagate information to a specific node, averaged over 1000 or 100 runs), and the relationship between this average propagation delay and the link distance from the central node.
| Type of Network | Network Size | |
| Network C (blue) | Work communication (military) | 18 |
| Network J (green) | Work communication (scientific) | 20 |
| Network M (red) | Work communication (scientific) | 63 |
| Network N (pink) | Internet newsgroup (Section 3) | 343 |
Table 13: Networks Used for Information Propagation Study
Figure 13 shows the results for networks C, J, and M. For these networks, the average propagation delay approximately fits the line:
The correlation here is 0.87 (r-squared = 0.76). The slope of the line is not significantly different if these networks are examined in isolation (p = 0.8).
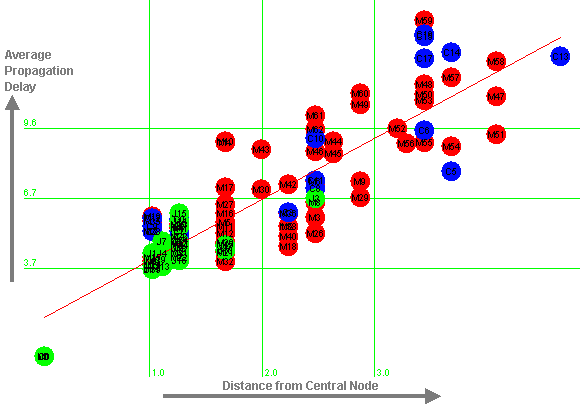 |
Figure 13: Distance from Central Node against Average Propagation Delay for Three Networks
Treating the fourth network (the case study from Section 3) in the same way, the line of best fit is slightly different, and the correlation is a slightly lower 0.82 (r-squared = 0.67):
The slope of this line, shown in Figure 14, is significantly different from the first three networks (p = 0.002). This is because the propagation delay is also influenced by the average number of outgoing links from network nodes, i.e. the more people one speaks to, the more likely one is to pass on the item of information to someone. This factor tends to be consistent for the three work communication networks, but not for the newsgroup network in Section 3, which has a very different nature. However, given a specific network, these experiments justify using link distance as an approximate indication of the time to propagate information. We expect those people who are far from the central node (in terms of link distance) to be the last to hear the latest news, gossip, etc. We also expect this relationship to be approximately linear.
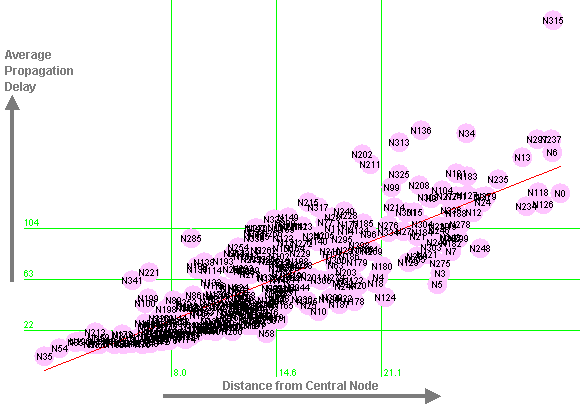 |
Figure 14: Distance from Central Node against Average Propagation Delay for Newsgroup Network
6. Other Forms of Distance
Link distance is not the only form of conceptual distance useful for Social Network Analysis. In this section, we examine two other forms of conceptual distance: activity-similarity distance and cultural distance. We show how insight into a network can be obtained by studying the statistical relationship between link distance and other forms of distance.
6.1. Activity-Similarity Distance
The study referred to in this section [5, 6] involved a military organisation which consisted of seven main subgroups (labelled A to G in Figure 15 and Figure 16). Extensive communication took place between all groups, but the strongest communication links were within the cluster of groups A (red), E (orange), and F (green); and within the cluster of groups C (blue), D (yellow), E (orange), and F (green). Figure 15 illustrates these communication patterns.
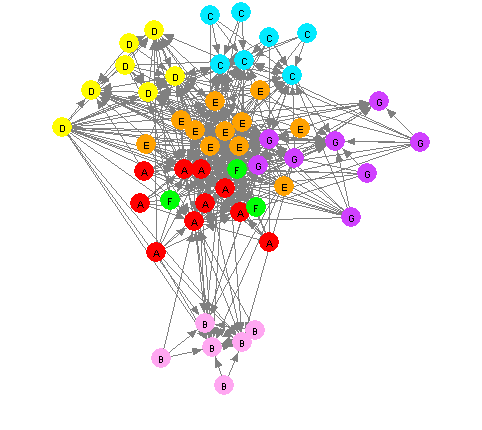 |
Figure 15: Spring-Embedding Layout for a Military Organisation
Participants in this study were asked to rate the relevance to their work of 15 topics. Principal Components Analysis was applied to the results, and three important factors were identified (these were in fact the second, third, and fourth principal components, since the first principal component indicated merely a general tendency to score all 15 topics highly). Figure 16 illustrates the result of Principal Components Analysis, with the X, Y, and Z coordinates of the three-dimensional figure reflecting the values of the three important factors. The lines in Figure 16 indicate the links in the social network. Link value in Figure 16 is indicated by line transparency (opaque lines have higher link value), but since physical location is being used to show the result of Principal Components Analysis, the length of the lines is unrelated to link value or link distance.
Clicking on the diagram in Figure 16 provides an animation which shows the relationships more clearly. There is a visible tendency for members of the same group to cluster loosely together, i.e. to have similar (but not identical) values for at least two of the three factors. If F(A), G(A), and H(A) are the values of the three factors resulting from Principal Components Analysis for person A, then we define the activity-similarity distance between two people A and B as:
Since the three factors are exactly the three dimensions X, Y, and Z of Figure 16, activity-similarity distance is identical with three-dimensional Euclidean distance in Figure 16. The smaller this distance between two people, the more similar is their work (as measured by the relevance of the 15 topics in the study), and the closer together they are in Figure 16. Groups A (red) and B (pink) are particularly close in terms of activity-similarity distance, as are groups D (yellow) and E (orange).

Figure 16: Activity-Similarity Distance based on Principal Components Analysis (click for GIF animation)
Activity-similarity distance tends to correlate with link distance, but in this study the correlation is weak (only 9% of the variance in link distance is explained, a correlation of 0.31). In other words, most communication did not occur between people working on similar topics. Although weak, the correlation is highly significant (p < 0.000001). The weakness of the correlation is unusual: in other studies that we have conducted, it is precisely people conducting similar activities who communicate the most. The weakness of the correlation may reflect either limitations of the activity survey (the list of 15 topics may not have been adequate), or it may reflect the complex nature of the work in this organisation, involving the integration of many different activities.
Conducting an analysis in the style of Section 3, we find that centrality explains 50% of the variance in link distance. This is less than the 70% of Figure 11, because this was not a "star-shaped" organisation. Centrality together with group average link distances explains 83% of the variance (a correlation of 0.91). This is even better than the 81% explanation of link distance in Figure 11, and indicates that we understand communication in this organisation fairly well. Activity-similarity distance does not explain any additional variance, i.e. the effect of activity-similarity distance on link distance is mediated by group membership.
Examining the variance in centrality scores, 39% is explained by military rank (more senior staff tend to be more central). We can provide a fairly accurate estimate of how much people communicate using the out-degree (sum of outgoing links). Out-degree predicts 47% of the variance in centrality (bigger communicators tend to be more central), and rank and out-degree together predict 65% of the variance in centrality. When group average centrality is taken into account, 69% of the variance in centrality is predicted (a correlation of 0.83).
Figure 17 illustrates the resulting statistical model in the style of Figure 11, i.e. green boxes show variables which are properties of individual people, while blue boxes show variables which are properties of pairs of people.
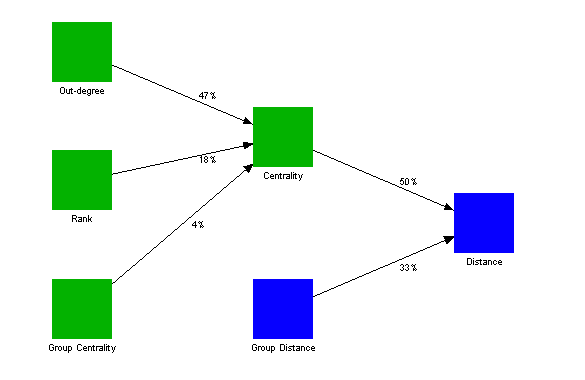 |
Figure 17: Statistical Model for Predicting Link Distance
Communication in this organisation is almost entirely a function of centrality and group identity, and centrality in turn is largely dependent on rank and amount of communication. Activity-similarity distance has an effect, but is mediated by group membership.
6.2. Cultural Distance
Our final study is based on the concept of cultural distance. We assessed a set of 22 countries (shown in Figure 18) on several criteria, including religion, language, economics, and military alliances such as NATO. From this we derived a measure of cultural distance, using techniques similar to the derivation of activity-similarity distance in the previous section. A more sophisticated concept of cultural distance can be obtained using the work of Hofstede [17], but the simple measure that we have used is sufficient for illustrative purposes.
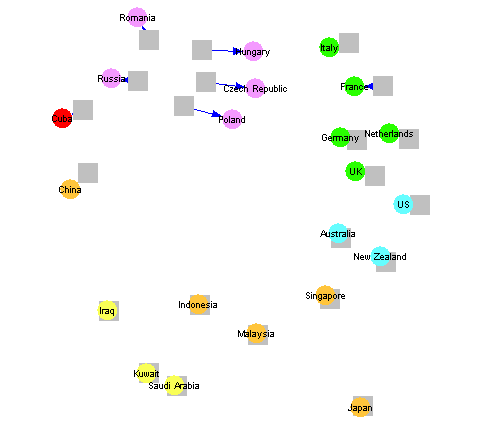 |
Figure 18: Social Flow Diagram for End of Cold War
Figure 18 provides a multi-dimensional scaling of our cultural distance measure, so that countries that are physically close together in Figure 18 have similar cultures. Figure 18 in fact shows two sets of cultural distances: one based on the situation during the Cold War, and the other after the end of the Cold War. Grey boxes represent the situation during the Cold War, while coloured circles represent the situation after the fall of the Soviet Union. Corresponding points are linked with arrows, producing what we call a social flow diagram [6]. The top left of Figure 18 shows how some former Communist countries have moved closer to Western Europe, while others have not.
A social flow diagram such as Figure 18 provides a way of visualising the relationship between two kinds of distance. It therefore provides a very useful alternative to the kind of regression analysis shown in Figure 10. We have found social flow diagrams useful in visualising the change in link distance before and after some form of management intervention. When the management intervention results in groups of individuals communicating more strongly with each other, the social flow diagram shows a group of converging arrows. On the other hand, if intervention results in groups of individuals communicating less strongly with each other, the social flow diagram shows a group of diverging arrows, as in the top left of Figure 18.
Cultural distance may also be correlated with link distance. In multicultural organisations, it is useful to assess cultural distance (using whatever measure is convenient) and study its relationship with link distance, using exactly the same method as for activity-similarity distance in the previous section. This can often shed great light on communication patterns in an organisation and reveal possible cases of problems due to cultural conflict.
7. Conclusions
In this paper we have argued for an approach to Social Network Analysis based on a concept of distance between people. Distance is a concept the human brain is skilled at thinking about and visually judging.
We have shown how to take a pseudo-logarithmic coding of link value and (generalising the concept of geodesic distance) transform it to a notion of link distance. This concept of link distance has five advantages:
- It can be computed efficiently, using the algorithms of Floyd, Dijkstra, or (more efficiently) Johnson [11].
- It can be easily visualised by spring-embedding (equivalent to Multi-Dimensional Scaling [12]), as shown in Figure 1 and Figure 2.
- Link distances are approximately normally distributed (as shown in Table 1). This means that standard statistical techniques can be used to study link distance.
- Link distances do not change radically if some people fail to complete survey forms, as discussed in Section 4.
- Link distance correlates with the time to propagate information through the network from the most central node, as discussed in Section 5.
In Section 3 we illustrated the use of link distance to analyse Social Networks by means of an Internet Newsgroup case study, obtaining the statistical model in Figure 11. Link distance is often significantly determined by the centrality of nodes, particularly for "star-shaped" networks. In Section 3 we also presented a definition of valued centrality which is more stable than the definition of closeness centrality [1]. We examined some factors which determine valued centrality, such as amount of communication, personal characteristics, military rank, and group membership.
Link distance is often also partly determined by other concepts of distance between people, such as similarity of activities or cultural distance. Section 6 discussed two examples of this. Determining the factors which statistically determine link distance forms the basis for an understanding of communication patterns. This can then lead to appropriate management activities to improve communication. We believe that this distance-based approach to Social Network Analysis, which integrates the toolkit of statistical techniques traditionally used in the Social Sciences, together with concepts of graph theory [2, 3], offers great promise in understanding and improving communication within organisations.
8. Acknowledgements
The CAVALIER software utilises the JAMA linear algebra module from the US National Institute of Standards and Technology; statistical routines by Bryan Lewis and Leigh Brookshaw; and image-processing code by Jef Poskanzer. The author is indebted to Dawn Hayter for many discussions on Social Network Analysis, and to two anonymous referees for comments on earlier drafts of this paper.
9. References
[1] Stanley Wasserman and Katherine Faust. Social Network Analysis: Methods and Applications, Cambridge University Press, 1994.
[2] Alan Gibbons. Algorithmic Graph Theory, Cambridge University Press, 1985.
[3] David Krackhardt. "Graph Theoretical Dimensions of Informal Organizations," Computational Organization Theory, pp 89-111, Kathleen M. Carley and Michael J. Prietula eds, Lawrence Erlbaum Associates, Hillsdale, NJ, 1994.
[4] Linton C. Freeman. "Visualizing Social Networks," Journal of Social Structure 1(1), February 2000. Available electronically at http://www.cmu.edu/joss/content/articles/volume1/Freeman.html
[5] Anthony H. Dekker. "Social Network Analysis in Military Headquarters using CAVALIER," Proceedings of 5th International Command and Control Research and Technology Symposium, Australian War Memorial, Canberra ACT, Australia, 24-26 October 2000. The full text of the paper is available electronically at http://www.dodccrp.org/events/2000/5th_ICCRTS/cd/papers/Track6/039.pdf
[6] Anthony H. Dekker. "Visualisation of Social Networks using CAVALIER," Proceedings of the Australian Symposium on Information Visualisation, Sydney, Australia, 3-4 December 2001, pp 49-55. Conferences in Research and Practice in Information Technology 9, Peter Eades and Tim Pattison, eds. Available electronically at http://crpit.com/confpapers/CRPITV9Dekker.pdf
[7] Anthony H. Dekker. "A Category-Theoretic Approach to Social Network Analysis," Proceedings of Computing: The Australian Theory Symposium, Melbourne, Australia, Jan-Feb 2002. Electronic Notes in Theoretical Computer Science 61, James Harland, ed. Available electronically at http://www.elsevier.com/locate/entcs/volume61.html
[8] Mark Granovetter. "The Strength of Weak Ties: a network theory revisited," Sociological Theory 1:201-233, 1983.
[9] Claude Flament. Applications of Graph Theory to Group Structure. Prentice-Hall, 1963.
[10] Song Yang and David Knoke. "Optimal Connections: Strength and Distance in Valued Graphs," Social Networks 23(4):285-295. October 2001.
[11] Thomas H. Cormen, Charles E. Leiserson, and Ronald L. Rivest. Introduction to Algorithms. MIT Press, 1990.
[12] Ulrik Brandes. "Drawing on Physical Analogies," In Drawing Graphs: Methods and Models, pp 71-86 (Michael Kaufmann and Dorothea Wagner, eds) Springer Verlag LNCS 2025, 2001.
[13] E. S. Keeping. Introduction to Statistical Inference. Van Nostrand, 1962.
[14] Ronald Jay Cohen, Mark E. Swerdlik, and Suzanne M. Phillips. Psychological Testing and Assessment, 3rd edition, Mayfield, 1988.
[15] Ulrik Brandes. "A Faster Algorithm for Betweenness Centrality," Journal of Mathematical Sociology 25(2):163-177, 2001. Available electronically at http://www.inf.uni-konstanz.de/algo/publications/b-fabc-01.pdf
[16] Carl G. Jung. Psychological Types. Routledge, 1991 (originally published 1921).
[17] Geert Hofstede. "Motivation, Leadership and Organization: Do American Theories Apply Abroad?" In Organization Theory: Selected Readings, Fourth Edition (Derek Pugh, ed) Penguin 1997.