JoSS Article: Volume 9
Going the Wrong Way on a One-Way Street:
Centrality in Physics and Biology*
Linton C. Freeman, lin@aris.ss.uci.edu
University of California, Irvine
Abstract
When ideas and tools move from one field to another, the movement is generally from the natural to the social sciences. In recent years, however, there has been a major movement in the opposite direction. The idea of centrality and the tools for its measurement were originally developed in the social science field of social network analysis. But currently the concept and tools of centrality are being used widely in physics and biology. This paper examines how and why that―wrong way―movement developed, its extent and its consequences for the fields involved.
Introduction
More than 170 years ago August Comte (1830-1842/1982 ) defined a hierarchy of the sciences. He claimed that as the oldest science, astronomy belonged at the foundation. Astronomy was followed by physics, chemistry and biology in that order. And finally, he placed sociology (by which he meant what we now call social science) at the top of his hierarchy.
Comte argued that each of the sciences tends to borrow concepts and tools from those that fall below it. Thus, physics borrows from astronomy; chemistry borrows from physics and astronomy and so on. From this perspective, then, borrowing is a one-way street; it goes from the older, more established sciences to the newer, less established ones.
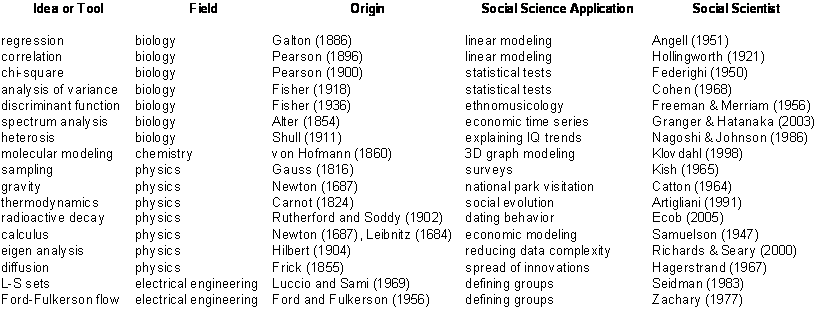
For the most part, Comte seems to have been right. Most, but not all, of the borrowing apparently has involved social scientists adopting tools and concepts developed by natural scientists. As Table 1 shows, it is quite easy to come up with examples in which social scientists have borrowed from biologists, chemists and physicists ― even from electrical engineers. On the other hand, it is hard to find examples where ideas and tools have moved from social science to biology chemistry or physics. One example is the graph theoretic concept of "clique." It was defined by Luce and Perry (1949) who were working on a project in social network analysis. And it is used in physics (e. g. Marco, 2007) and biology (Wang, 2008).
|
Table 1. Some Examples of Applications in Social Science
that were Borrowed from Other Sciences.
|
In the present paper, I will describe a recent phenomenon, one in which a good many ideas and tools have moved from social science to the natural sciences. Specifically, I will show that, although they were developed in social science, concepts and tools related to centrality have been adopted and are widely used in physics and particularly in biology.
The Origins of the Idea of Centrality
It has been argued (Holme, Kim, Yoon and Han, 2002) that the notion of centrality was introduced by the eminent French mathematician, Camille Jordan. It is true that Jordan (1869) did propose two procedures for determining the centers of graphs. But his procedures do not correspond to contemporary ideas about centrality.
Jordan's centers depart from current usage in two ways. First, they are restricted to graphs that take the form of trees; they were not defined for more general forms of graphs. And second, Jordan's procedures are essentially categorical. They do not address the issue of measuring the degree of centrality of any node. Instead, each procedure simply picks out one, or at most two, nodes and specifies them as centers.
One of Jordan's centers, for example, involves calculating the geodesic distance between each node and all of its reachable neighbors. From these results, the distance to its farthest neighbor can be determined. This information, that has come to be called the "eccentricity" of a node, has traditionally been used solely to determine which node or nodes display the least eccentricity and are, therefore, the center or centers of the graph.[1]
In contrast, the procedures developed in social science apply to all graphs and they provide measures of centrality for every node in a graph. They first emerged in the late 1940s in the Group Networks Laboratory at MIT. There, Alex Bavelas and his students - particularly Harold Leavitt - conducted a series of experiments on the impact of organizational form on productivity and morale (Bavelas, 1948, 1950; Leavitt, 1951). The experimental variable that they manipulated was the centrality of each experimental subject in the pattern of communication linking them.
The MIT group proposed several procedures for measuring the centrality of nodes in graphs, but the simplest - the one that is still used - is based on the sum of the geodesic (shortest path) distances from each node in a connected graph to all the other nodes in that graph. This measure may be applied, not just to trees, but to any connected graphs. Moreover, it does not simply specify a collection of "centers." Instead, it yields an index of centrality for every node in any connected graph.
Centrality in Social Science
Following this first work a large and confusing array of other proposals for measuring centrality were introduced. I sifted through those proposals and came up with three measures of centrality that together seemed to capture the essential elements in all the earlier work (Freeman, 1979). One was based on the closeness of a node to all the other nodes in a connected graph. The second was based on the degree of a node - the number of others to which it was directly connected.[2] And the third was based on the betweenness of a node. A given node's betweenness is determined by examining the shortest paths linking all other pairs of nodes in the graph and tabulating the number of those paths on which the node in question falls. Both degree centrality and betweenness centrality, then, can be calculated for all the nodes in any graph at all, connected or not.
All this work was grounded in graph theory. But during this same period, another set of procedures, based on matrix algebra, were being developed. Leo Katz (1953) introduced a "status" index based on the successive powers of an affiliation matrix. In the Katz measure, the centrality or status of an individual depends on the whole pattern of ties displayed in the affiliation matrix. Each individual's status depends on the number of ties that individual has to others, the number of ties each of those others has, and so on. Each successive ring of ties makes a diminishing contribution to the status of the original individual, but they all do contribute.
In a paper that was primarily focused on uncovering social groups, Charles Hubbell (1965) extended Katz's status index. And Phil Bonacich (1972, 1987) characterized both the Katz index and the Hubbell index as measures of centrality. He showed, moreover, that both were determined by the first eigenvector of the data matrix.
Beginning in about 1980 then, the measures based on closeness, degree, betweenness and the first eigenvector became standard in social network analysis. All four were widely used in the field. But, in 1998, there was a revolution in social network analysis; since then nothing has been the same.
The Revolution
The world of research in social network analysis was changed dramatically when a young physicist-engineer, Duncan Watts, working with a mathematician, Steven Strogatz, published a paper in Nature. Their paper was titled, "Collective dynamics of 'small world' networks" and it took up a topic that traditionally had been a core part of social network research. It introduced a new model that was designed to account for the small world experience in social life.
On the face of it, the Watts and Strogatz paper might be taken as an example of movement from social science to natural science. But the fact is that it drew nothing beyond the pop phrase "small world" from our literature. Although the social network literature about the small world included formal models (e. g. Pool and Kochen, 1978; White, 1970) they were not cited in the Watts and Strogatz article. Indeed, the concepts and tools that were proposed in their paper were all brand new.
Other physicists had already been involved in social network analysis. Notable among these were Derek de Solla Price, Harrison White and Peter Killworth (e. g. Price, 1965, 1976; White, 1970; White, Boorman and Breiger, 1976; Killworth, McCarty, Bernard, Johnsen, Domini and Shelley, 2003; Killworth, McCarty, Bernard and House, 2006). These physicists read the social network literature, joined the collective effort and contributed to an ongoing research process. But Watts and Strogatz did none of these things. Their paper simply took a research topic that had been a part of social network analysis and implicitly redefined it as a topic in physics.
The strange thing about all this is that, apparently, other physicists agreed. Very soon there were more publications about small worlds in physics journals than there were in social science journals. Figure 1 shows the situation in 2003 with respect to publications on the small world theme. Each node is an article and each edge represents a citation linking a pair of articles. Black nodes are physicists, white nodes are members of the social network community and gray nodes are outsiders. In the five years between 1998 and 2003 physicists turned out more publications on the subject than members of the social network community had produced over a period of 45 years. And, as the figure shows, members of the two camps seemed for the most part to avoid citing one another; few citations crossed the boundary between physics and social science.
The physicists were quick to extend the range of their interests to include other topics traditionally associated with research in social network analysis. And, for the most part, they continued to ignore earlier work by social network analysts. Three physicists, Barabasi, Albert and Jeong (1999), for example, published a paper in Physica A in which they examined the distribution of what network analysts had been calling "degree centrality." But they talked only about "degree distributions" and made no mention of centrality. Apparently, they were unaware of related work by network analysts (e. g. Price, 1976).
Two years later Jeong, Mason, Barabasi and Oltvai (2001) published a letter in Nature. Again they were concerned with degree distributions, and although they still did not cite research in social network analysis, this time they did use the word "centrality" in the title of their paper.
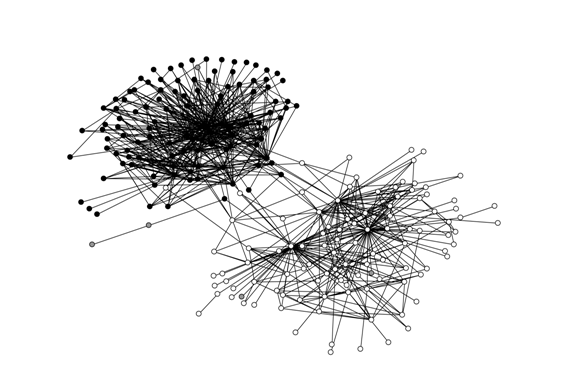
Figure 1. Small World Publications circa 2003 (Freeman, 2004, p. 166).
Bridging Social Science and Physics
In 1999 Watts made an attempt to move ideas from physics to social science. By publishing an article in the American Journal of Sociology (Watts, 1999), he introduced his physicist's conception of the small world problem to the social science community. In that article he mentioned centrality and several other social network concepts and tools, but for the most part he disparaged them. He suggested, for example, that the "computational costs" of calculating betweenness centrality were likely to be "prohibitive." Watts' effort was designed to move concepts in the traditional direction. He introduced an idea from physics into the social science literature. But he made no attempt to introduce centrality or any other social science ideas into physics.
The first explicit movement in the other direction―the "wrong way"―was made by another physicist, Mark Newman. Newman read Wasserman and Faust's (1994) text on social network analysis and was struck by the potential utility of the notion of betweenness centrality. He used betweenness centrality in a study of collaboration among scientists that was published in a physics journal, Physical Review E (Newman, 2001). In that paper Newman cited my derivation of betweenness (Freeman, 1977).
The physics community was quick to pick up on Newman's article. That same year, Goh, Ki, Kahng and Kim (2001) published a paper in Physical Review Letters. They examined the distribution of betweenness centrality and they thanked Newman for calling their attention to the research in social network analysis. And by the following year, physicists Holme, Kim, Yoon and Han (2002) published an article in Physical Review E that reviewed all three graph theoretic measures of centrality - degree, closeness and betweenness - and thereby made them a part of the physics literature.
Centrality in Biology
The first application of centrality ideas to a topic in biology was made by physicists. The letter in Nature by the physicists, Jeong, Mason Barabasi and Oltvai (2001) that was mentioned above, did not cite social network literature. But it did apply a degree based measure of centrality to a problem in biology.
Structural biologists themselves also began to use centrality that same year. In 2001 two biologists, Wagner and Fell, published a paper on metabolic networks in the Proceedings of the Royal Society of London, Series B, Biological Science. In it, they used degree and closeness as indicators of centrality, but, like Jeong et al. they made no mention of the social network literature on the subject
The very next year, however, four molecular biophysicists, Vendruscolo, Dokholyan, Paci and Karplus (2002) followed up by publishing an article on proteins in Physical Revue E. In it they used betweenness centrality and cited my 1977 paper. Then two systems biologists, Ma and Zeng (2003) followed up a year later when they discussed all three graph theoretic measures.
It was two more years before both the physicists and the biologists adopted Bonacich's first eigenvector as a measure of centrality. A computational biologist, Estrada and a mathematician, Rodriguez-Velásquez, published a joint paper on centrality in Physical Review E. Their publication was in a physics journal, but their applications were drawn from biology. So, by 2005, all four of the centrality measures from social network analysis had moved - the wrong way - into both physics and biology.
Figure 2 shows the number of articles involving centrality that were published each year in social science and in physics and biology. In social science there was a small surge during the late 1950s and the early 1960s and another beginning in the early 1990s. The former resulted from a widespread interest in the MIT experiment by Bavelas and Leavitt and the latter is due to the growing use of centrality in studies of management and organizational behavior. The striking feature of Figure 2, however, is the steep growth of centrality publications in physics and biology since the early 2000s. Once it started, research based on centrality in these two fields quickly outpaced that conducted in social network analysis.
This sudden surge in centrality publications in physics and biology raises questions about how centrality is used in those fields. In the next section I will review some of their applications.
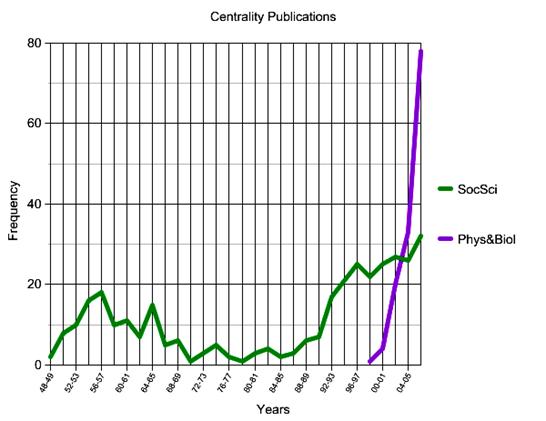
Figure 2. The Production of Centrality Literature by Field.
Applications of Centrality in Physics and Biology
Many of the data sets that physicists and biologists have used to look at centrality are immediately recognizable to social network analysts. The data simply are social networks. Newman (2003), for example studied friendships linking students. And both Newman (2003) and Albert and Barabasi (2002) reported data on human sexual contacts. Holme, Liljeros, Edling and Kim (2003) described contacts among prison inmates, and Holme, Huss and Jeong (2003) as well as Newman (2003) referred to email messages. Newman (2003) and Albert and Barabasi (2002) also talked about telephone calls.
In addition, Girvan and Newman (2002), Holme, Huss and Jeong (2003) and Estrada and Rodriguez-Velázquez (2006) studied data on collaboration among scientists. Newman (2003), Albert and Barabasi (2002) and Estrada and Rodriguez-Velázquez (2006) examined citation patterns. Other studies have dealt with corporate interlock (Newman, 2003; Estrada and Rodriguez-Velázquez, 2006). And Kitsak, Havlin, Paul, Riccaboni, Pammolli and Stanley (2007), Song, Havlin and Makse (2005) along with Newman (2003) and Albert and Barabasi (2002) have examined the World Wide Web. In addition, linguistic data sets have been examined (Albert and Barabasi, 2002; Newman, 2003; Estrada & Rodriguez-Velázquez, 2005).
Finally, physicists and biologists have even reanalyzed some of the classic social network data sets. Girvan and Newman (2002), Holme, Huss and Jeong (2003) and Kolaczyk, Chua and Barthelemy (2007) have used Zachary's (1977) karate club data and Newman (2006) analyzed Padgett's (1993) data on Florentine families.
Physicists have also given some attention calculating centralities on data that outsiders might think of as belonging to physics proper. Prominent among these are studies of packet switching in the internet (Holme, Kim, Yoon and Han, 2002; Holme, Huss and Jeong, 2003; Albert and Barabasi, 2002; Estrada & Rodriguez-Velázquez, 2005; Kitsak, Harlin, Paul, Pammolli and Stanley, 2007; Kolaczyk, Chua and Barthelemy, 2007), the electrical power grid (Barabasi, Albert and Jeong, 1999; Albert and Barabasi, 2002; Govindaraj, 2008) and electronic circuitry (Newman, 2003).
But by far the most effort has gone into applying centrality to various problems from biology. In biological research, centrality has been applied to three main kinds of networks, connections among amino acid residues, protein-protein interaction networks and links in metabolic networks. These three research efforts will be examined below.
Amino acids are molecules that are the building blocks for constructing proteins. They link together to form long chains, called polypeptides. When they link they lose the elements of water and are thereafter called amino acid residues. Polypeptides are linear chains, but in order to turn into proteins they must fold into three dimensional forms. An example of a polypeptide folding into a protein is shown in Figure 3.
Proteins can be represented as graphs. The nodes in the graph of a protein are the amino acid residues it contains. When two residues are in close physical proximity, their proximity is viewed as evidence that they are linked by some sort of chemical interaction. Thus, any pair of residues is defined as linked whenever they are closer together than some specified criterion distance.
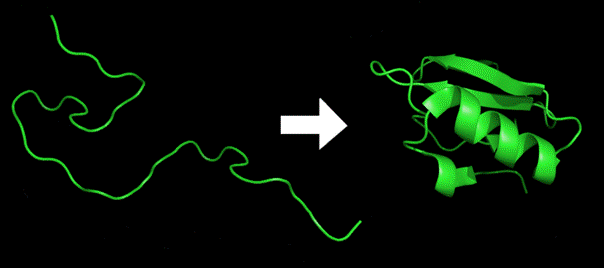
Figure 3. An Example of Protein Folding (from Wikipedia).
In any particular case, a polypeptide may fold properly and turn itself into the appropriate protein or it may fail to do so. Since errors in folding can lead to disease or death, proper folding is critical. Experimental research has established that only a small number of the amino acid residues that make up a polypeptide are critical for its proper folding.
Earlier experimental results had shown, for example, that only two residues were critical in the folding of the protein 1AYE. Vendruscolo, Dokholyan, Paci and Karplus (2002) hypothesized that betweenness centrality might pick out those critical residues. Figure 4 shows their results for the residues that are folded to make 1AYE. The betweenness of each residue is shown by the height of the curve and the two critical residues are marked with squares.
The authors concluded, therefore, that betweenness general provided a good way to find the residues that were critical to proper protein folding. But, following up, del Sol, Fujihashi, Amoros and Nussinov (2006) argued that closeness centrality was more effective than betweenness in picking out the critical residues. And Chea and Livesay (2007) went on to show that in a large sample of proteins closeness centralities were statistically significant in their ability to determine which residues were critical.
A second research area in biology in which centralities have been applied is in the study of protein-protein interaction (PPI) networks. Interactions linking proteins are common. They play an important part in every process involving living cells. Knowledge about how proteins interact can lead to better understanding of a great many diseases and it can help in the design of appropriate therapies.
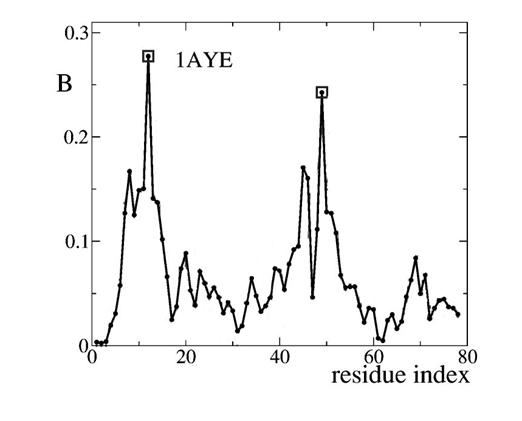
Figure 4. The Residues That Are Folded to Make Protein 1AYE
Often studies of PPI networks generate huge data sets. In the letter in Nature that was mentioned above, Jeong, Mason, Barabasi and Oltvai (2001) examined a data matrix that contained 2440 interactions linking 1870 proteins contained in yeast. Earlier experimental work had demonstrated that some of the protein molecules in yeast were lethal; if they were removed the yeast would die. Removing others, however, had no such dramatic effect. So Jeong et al. examined the question of whether the structural properties of those proteins - in particular, their degree centralities - could predict which proteins were lethal and which ones were not. Their results showed that proteins of high degree were far more likely to be lethal than those of lower degree. Follow-up research (e. g. Coulomb, Bauer, Bernard and Marsolier-Kergoat, 2005; Han, Dupuy, Bertin, Cusick and Vidal, 2005), however, showed that gaps in the PPI data were enough to cast doubt on that result.
Nonetheless, centralities in PPI networks continued to be studied. Joy, Brock, Ingber and Huang (2005) also studied centralities in the PPI networks of yeast. Their results showed that proteins that combined low degree with high betweenness were those that were likely to be essential to the survival of the yeast. They found, moreover, that the evolutionary ages of individual yeast proteins was positively correlated with their betweenness centrality.
Hahn and Kern (2005) extended the PPI network analysis to other forms of life. They studied PPI networks in yeast, in worms and in flies. They reported that the patterns of networks linking proteins in all three species had "remarkably" similar structural forms. Regardless of their degree centralities, proteins with high betweenness turned out to evolve more slowly and were more likely to be essential for survival.
The third major application of centrality in biology is in the study of metabolic networks. These metabolic networks are formed within cells. They include all the chemical reactions that allow cells to process metabolites. Metabolites include the nutrients that start the process, intermediate compounds and end products. Thus, metabolites are connected in chains of reactions. And each cell contains a great many different chains. These different chains are essential for the life of the organism.
The use of centrality in the study of metabolic networks began in 2000 with a study by Fell and Wagner. They examined metabolic reactions in E. coli bacteria. In their data metabolites were defined as nodes and two metabolites were viewed as connected if the occurred in the same chain of reactions. They wanted to determine which metabolites were involved in the widest range of reactions, so they calculated the closeness centrality of each. Those closeness centralities were used to identify the extent of each metabolite's influence.
Three years later Ma and Zeng (2003) did a comparative study in which they examined the metabolic networks of 65 organisms. They used the social network computer program, PAJEK (Batagelj and Mrvar, 1998), to determine that metabolic networks typically embodied several strong components. They calculated degree and closeness centralities in the largest of those components and concluded that organisms from different domains of life display different patterns of closeness centralities.
Schuster, Pfeiffer, Moldenhauer, Koch and Dandekar (2002) sought to untangle the complexity of metabolic networks by removing the nodes of highest degree, and examining the "internal" structure of the resulting components. And a year later Holme, Huss and Jeong (2003) modified that approach. They reasoned that degree centrality was essentially a local index and they substituted a global one, betweenness. They constructed bipartite graphs for 43 organisms in which they defined two classes of nodes. One class consisted of molecules that are acted upon by reaction agents, the second represented chemical reactions. Directed lines link molecules to reactions.
This bipartite structure permitted them to eliminate only those nodes involved in reactions. That way they were able to create separate components and to simplify the overall structure. Because they used betweenness, they argued, they retained information on large scale structural patterns.
We saw above that the social network program, PAJEK, has been applied in research in biology. But the biologists' focus on centrality has also spawned the development of new computer programs. In 2006 Baitaluk, Sedova, Ray and Gupta of the San Diego Supercomputer Center released a new program, PathSys, designed to analyze biological networks. They considered betweenness centrality important enough in biological research that they featured it in their tutorial for the program. And that same year three molecular geneticists, Junker, Koschützki and Schreiber, released a JAVA program, CentiBiN. That program is designed for applications to biological networks, and all it calculates are 17 different kinds of centers and centralities
These,
then, are some examples that illustrate importance of centrality to physicists
and biologists. From these illustrative examples it should be clear that the
use of centrality concepts and tools is widespread in those fields,
particularly in biology. In the next and final section of this paper I will
provide a summary and present some conclusions.
Summary and Conclusions
I have shown here that applications of centrality have moved "the wrong way" from social science to physics and biology. Centrality was developed by social network analysts. But both physicists and biologists have borrowed the concepts and tools of centrality from social network analysis and applied them in their fields.
The physicists and biologists, moreover, have documented their borrowing by their citations to the social network literature. Figure 5, for example, shows citations to my 1977 article on betweenness centrality, by year and by field. It shows that, in recent years, citations to that article from physics and biology have completely overwhelmed those from social science.
Given that ideas and tools involving centrality have moved the "wrong way" from social science to physics and biology, we are left with the problem of explaining why such a movement took place. Probably the single most important factor leading to this wrong way movement resulted from an explosive growth, in both physics and biology, in research that focused, not on objects as such, but on the connections that link objects together. In both of these fields, scientists quite suddenly developed a major interest in networks - all kinds of networks.
This expanding interest in networks apparently grew out of two relatively recent developments. By the year 2000, both physicists and biologists were faced with huge amounts of readily accessible relational data and, at the same time, they had easy access to large-scale computing power. As Bornholdt and Schuster (2002) put it:
Triggered by recently available data on large real world networks (e.g. on the structure of the internet or on molecular networks in the living cell) combined with fast computer power on the scientist's desktop, an avalanche of quantitative research on network structure currently stimulates diverse scientific fields.
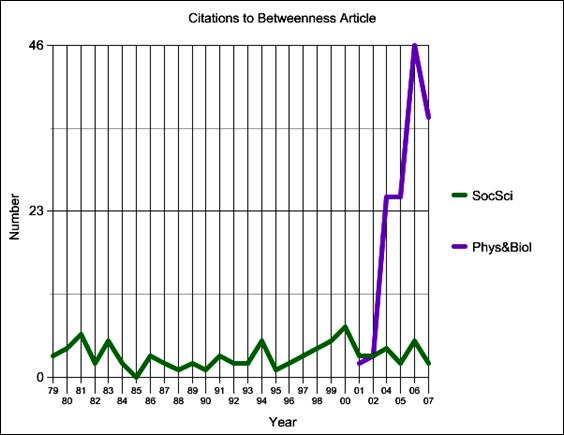
Figure 5. Citations to Freeman (1977) by Year and by Field
Particularly in biology, research scientists were desperate for tools that could be used to analyze network data. They had recently been faced with a huge and ever growing collection of network data stemming from all the work on genome sequencing. Two biologists, Wagner and Fell (2001), described the situation:
The information necessary to characterize the genetic and metabolic networks driving all functions of a living cell is being put within our reach by various genome projects. With the availability of this information, however, a problem will arise which has, as yet, been little explored by molecular biologists: how to adequately represent and analyse the structure of such large networks.
Thus, biologists, and probably physicists too, came upon centrality at the point of their greatest need for analytical tools that could be used to uncover important structural properties of networks. The centrality ideas from social network analysis are simple and easy to grasp. They are intuitively appealing and their structural implications are clear. They have, moreover, been formalized using mathematical tools no more difficult than graph theory and elementary matrix algebra. Thus, centralities are the natural choice for anyone seeking to uncover positions in a new area of application. And they turn out to be the tools that were actually chosen for that purpose by biologists and physicists.
As a final note, I would like to stress that almost all of the applications of centrality in biology have involved interplay between physicists and biologists. A collection of physicists, Jeong, Mason, Barabasi and Oltvai (2001) were the first to use centrality in the study of interactions among proteins. But the idea was picked up and refined by four biologists, Joy, Brock, Ingber and Huang (2005) and again by two more biologists, Hahn and Kern (2005). On the other hand, the use of centrality in cell metabolic research began with two biologists, Fell and Wagner (2000) and was later extended by three physicists, Holme, Huss and Jeong (2003). In all of this research biologists and physicists have managed to work on common problems. And they have done it in a way that allows representatives of both fields to contribute freely to the overall collective effort.
With respect to social network analysts, the physicists have given every indication that they want to build the same kind of cooperative relationship that they have with biologists. They have explored social network research problems, they have analyzed social network data sets, they have cited social network publications and they have even refined and extended tools for the analysis of centrality (e. g. Girvan and Newman, 2002).
There is every reason to believe that a cooperative relationship between these two fields would yield benefits for both. But, so far, a great many network analysts have tended to view the physicists as interlopers, invading our territory. I suggest, instead, that we welcome the contributions of the physicists and build on them. That seems to have worked for the biologists and it should work for us.
References
Albert, R. and A. L. Barabasi (2002). "Statistical mechanics of complex networks." Reviews of Modern Physics 74 (1): 47-97.
Alter, D. (1854). "On certain physical properties of light produced by the combustion of different metals in an electric spark refracted by a prism." American Journal of Science and Arts 18: 55-57.
Angell, R. C. (1961). "The moral integration of American cities." American Journal of Sociology 53: 1-140.
Artigliani, R. U. (1991). "Social evolution: a non-equilibrium systems model." Ed. E. Laszlo. The New Evolutionary Paradigm. New York, Gordon and Breach.
Baitaluk, M., M. Sedova, et al. (2006). "Biological Networks: visualization and analysis tool for systems biology." Nucleic Acids Research 34: W466-W471.
Barabasi, A. L., R. Albert, et al. (1999). "Mean-field theory for scale-free random networks." Physica A 272 (1-2): 173-187.
Batagelj, V. and A. Mrvar (1998). "Pajek-Program for large network analysis." Connections 21 (2): 47-57.
Bavelas, A. (1948). "A mathematical model for small group structures." Human Organization 7: 16-30.
Bavelas, A. (1950). "Communication patterns in task oriented groups." Journal of the Acoustical Society of America 22 (6): 725-730.
Bonacich, P. (1972). "Factoring and weighting approaches to status scores and clique identification." Journal of Mathematical Sociology 2: 113-120.
Bonacich, P. (1987). "Power and centrality: A family of measures." American Journal of Sociology 92: 1170-1182.
Carnot, S. (1824/1960). Réflexions sur la Puissance Motrice du Feu. Mineola, N.Y., Dover.
Catton, W. R. J. and L. Berggren (1964). "Intervening opportunities and national park visitation rates." Pacific Sociological Revue 7: 66-73.
Chea, E. and D. R. Livesay (2007). "How accurate and statistically robust are catalytic site predictions based on closeness centrality?" BMC Bioinformatics 8, 153.
Cohen, J. (1968). "Multiple regression as a general data-analytic system." Psychological Bulletin 70: 426-443.
Comte, A. (1830-1842/1982). Cours de philosophie positive. Paris, Hatier.
Coulomb, S., M. Bauer, D. Bernard and M.-C. Marsolier-Kergoat (2005). "Gene essentiality and the topology of protein interaction networks." Proceedings of the Royal Society of London, B, Biological Sciences 272 (1573): 1721-1725.
del Sol, A., H. Fujihashi, et al. (2006). "Residue centrality, functionally important residues, and active site shape: Analysis of enzyme and non-enzyme families." Protein Science 15 (9): 2120-2128.
Ecob, E. (2005). The Dating Game: Looking for Mr./Mrs. Right. Physics. Oxford, Oxford MS degree.
Estrada, E. and J. A. Rodriguez-Velázquez (2005). "Spectral measures of bipartivity in complex networks." Physical Review E 72, 046105.
Estrada, E. and J. A. Rodriguez-Velázquez (2006). "Subgraph centrality and clustering in complex hyper-networks." Physica A-Statistical Mechanics and Its Applications 364: 581-594.
Federighi, E. (1950). "The use of chi-square in small samples." American Sociological Review 15: 777-779.
Fell, D. A. and A. Wagner (2000). "The small world of metabolism." Nature Biotechnology 18 (11): 1121-1122.
Fisher, R. A. (1918). "The correlation between relatives on the supposition of Mendelian inheritance." Transactions of the Royal Society of Edinburgh 52: 399-433.
Fisher, R. A. (1936). "The use of multiple measurements in taxonomic problems." Annals of Eugenics 7: 179-188.
Ford, L. R. and D. R. Fulkerson (1957). "A simple algorithm for finding maximal network flows and an application to the Hitchcock problem." Canada Journal of Mathematics 9: 210-218.
Freeman, L. C. (1977). "A set of measures of centrality based on betweenness." Sociometry 40: 35-41.
Freeman, L. C. (1979). "Centrality in social networks: Conceptual clarification." Social Networks 1: 215-239.
Freeman, L. C. (2004). The Development of Social Network Analysis: A Study in the Sociology of Science. Vancouver, BC, Empirical Press.
Freeman, L. C. (2008). Social Network Analysis. London: SAGE.
Freeman, L. C. and A. P. Merriam (1956). "Statistical classification in anthropology: An application to ethnomusicology." American Anthropologist 58: 464-472.
Frick, A. (1855). "On liquid diffusion." Philosophical Magazine 10: 30-39.
Galton, F. (1886). "Regression towards mediocrity in hereditary stature." Journal of the Anthropological Institute 15: 246-263.
Gauss, C. F. (1816/1880). "Bestimmung der Genauigkeit der Beobachtungen." Koenigliche Gesellschaft der Wissenschaften 4: 109-117.
Giovindaraj, T. (2008). "Characterizing performance in socio-technical systems: A modeling framework in the domain of nuclear power." Omega 36: 10-21.
Girvan, M. and M. E. J. Newman (2002). "Community structure in social and biological networks." Proceedings of the National Academy of Sciences of the United States of America 99 (12): 7821-7826.
Goh, K. I., B. Kahng, et al. (2001). "Universal behavior of load distribution in scale-free networks." Physical Review Letters 87, 278701.
Granger, C. W. J. and M. Hatanaka (1964). Spectral Analysis of Economic Time Series. Princeton, NJ, Princeton University Press.
Hage, P. and F. Harary (1995). "Eccentricity and centrality in networks." Social Networks 17(1): 57-63.
Hagerstrand, T. (1967). Innovation diffusion as a spatial process. Chicago, University of Chicago Press.
Hahn, M. W. and A. D. Kern. (2005). "Comparative genomics of centrality and essentiality in three eukaryotic protein-interaction networks." Molecular Biology and Evolution 22 (4): 803-806.
Han, J.-D., D. Dupuy, N. Bertin, M. E. Cusick and M. Vidal (2005). "Effects of sampling on topology predictions of protein-protein interaction networks." Nature Biotechnology 23 (7): 839-844.
Hilbert, D. (1904). "Grundzüge einer allgemeinen Theorie der linearen Integralgleichungen." Nachrichten von d. Königl. Ges. d. Wissensch. zu Göttingen.: 49-91.
Hollingworth, H. L. (1921). "Judgements of persuasiveness." Psychological Review 28: 4.
Holme, P., M. Huss, et al. (2003). "Subnetwork hierarchies of biochemical pathways." Bioinformatics 19 (4): 532-538.
Holme, P., B. J. Kim, et al. (2002). "Attack vulnerability of complex networks." Physical Review E 65, 056109.
Holme, P., F. Liljeros, et al. (2003). "Network bipartivity." Physical Review E 68, 056107.
Hubbell, C. H. (1965). "An input-output approach to clique identification." Sociometry 28: 377-399.
Jeong, H., S. P. Mason, et al. (2001). "Lethality and centrality in protein networks." Nature 411 (6833): 41-42.
Jordan, C. (1869). "Sur les assemblages de lignes" Journal für reine und angewandte Mathematik 70: 185-190.
Joy, M. P., A. Brock, et al. (2005). "High-betweenness proteins in the yeast protein interaction network." Journal of Biomedicine and Biotechnology 2005 (2): 96-103.
Junker, B. H., D. Koschützki, et al. (2006). "Exploration of biological network centralities with CentiBiN." BMC Bioinformatics 7: 219.
Katz, L. (1953). "A new status index derived from sociometric analysis." Psychometrika 18: 39-43.
Killworth, P. D., C. McCarty, H. R. Bernard, E. C. Johnsen, J. Domini and G. A. Shelley. (2003). "Two interpretations of reports of knowledge of subpopulation sizes." Social Networks 25: 141-160.
Killworth, P. D., C. McCarty, H. R. Bernard, and M. House. (2006). "The accuracy of small world chains in social networks." Social Networks 28: 85-96.
Kish, L. (1965). Survey Sampling. New York, Wiley.
Kitsak, M., S. Havlin, et al. (2007). "Betweenness centrality of fractal and nonfractal scale-free model networks and tests on real networks." Physical Review E 75, 056115.
Klovdahl, A. (1998). "A picture is worth . . . :Interacting visually with complex network data." Computer Modeling and the Structure of Dynamic Social Processes. W. Liebrand. Amsterdam, ProGamma.
Kolaczyk, E. D., D. B. Chua, et al. (2007). "Co-Betweenness: A Pairwise Notion of Centrality." Available: http://arxiv.org/abs/0709.3420 [September 25, 2008].
Leavitt, H. J. (1951). "Some effects of communication patterns on group performance." Journal of Abnormal and Social Psychology 46: 38-50.
Leibnitz, G. (1684/1969). "Nova methodus pro maximis et minimis." A Source Book in Mathematics, 1200 - 1800. Ed. D. J. Struik. Cambridge, MA, Harvard University Press: 271-281.
Lorrain, F., H. C. White. (1971). "Structural equivalence of individuals in social networks." Journal of Mathematical Sociology 1: 49 - 80
Luccio, F. and M. Sami (1969). "On the decomposition of networks into minimally interconnected networks." IEEE Transactions on Circuit Theory CT-16: 184-188.
Luce, R. D. and A. Perry (1949). "A method of matrix analysis of group structure." Psychometrika 14: 95-116.
Ma, H. W. and A. P. Zeng (2003). "The connectivity structure, giant strong component and centrality of metabolic networks." Bioinformatics 19 (11): 1423-1430.
Marco, B. and B. Paolo (2007). The Maximum Clique Problem in Spinorial Form, AIP.
Nagoshi, C. T. and R. C. Johnson (1986). "The ubiquity of g." Personality and Individual Differences 7: 201-207.
Newman, M. E. J. (2001). "Scientific collaboration networks. II. Shortest paths, weighted networks, and centrality." Physical Review E 64, 016132.
Newman, M. E. J. (2003). "The structure and function of complex networks." SIAM Review 45 (2): 167-256.
Newton, I. (1687/1999). Philosophiæ Naturalis Principia Mathematica. Berkeley, University of California Press.
Pearson, K. (1895-1896). "Contributions to the mathematical theory of evolution. III. Regression, heredity, and panmixia." Proceedings of the Royal Society of London 59: 69-71.
Pearson, K. (1900). "On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling." Philosophical Magazine 50: 157-172.
Pool, I. D. and M. Kochen (1978). "Contacts and influence." Social Networks 1 (1): 5-51.
Price, D. d. S. (1965). "Networks of scientific papers." Science 149 (3683): 510-515.
Price, D. d. S. (1976). "A general theory of bibliometric and other cumulative advantage processes." Journal of the American Society for Information Science 27: 292-306.
Richards, W. and A. Seary (2000). "Eigen Analysis of Networks" Journal of Social Structure 1 (2). Available: http://www.cmu.edu/joss/content/articles/volume1/RichardsSeary.html [September 25, 2008].
Rutheford, E. and F. Soddy (1902 ). "The cause and nature of radioactivity." Philosophical Magazine 4: 370-396.
Samuelson, P. A. (1948). Economics. New York, McGraw-Hill.
Schuster, S., T. Pfeiffer, et al. (2002). "Exploring the pathway structure of metabolism: decomposition into subnetworks and application to Mycoplasma pneumoniae." Bioinformatics 18 (2): 351-361.
Seidman, S. B. (1983). "Internal cohesion of LS sets in graphs." Social Networks 5: 97-107.
Shull, G. H. (1911). "The genotypes of maize." American Naturalist 45: 234-252.
Song, C. M., S. Havlin, et al. (2005). "Self-similarity of complex networks." Nature 433(7024): 392-395.
Vendruscolo, M., N. V. Dokholyan, et al. (2002). "Small-world view of the amino acids that play a key role in protein folding." Physical Review E 65, 061910.
von Hofmann, A. W. (1860). Cited in Wikipedia. Available: http://en.wikipedia.org/wiki/August_Wilhelm_von_Hofmann [September 25, 2008].
Wagner, A. and D. A. Fell (2001). "The small world inside large metabolic networks." Proceedings of the Royal Society, B, Biological Sciences 268: 1803-1810.
Wang, J., Z. Cai, et al. (2008). "An improved method based on maximal clique for predicting interactions in protein interaction networks." International Conference on BioMedical Engineering and Informatics: 62-66.
Wasserman, S. and K. Faust (1994). Social Network Analysis: Methods and Applications. Cambridge, Cambridge University Press.
Watts, D. J. (1999). "Networks, dynamics, and the small-world phenomenon." American Journal of Sociology 105 (2): 493-527.
Watts, D. J. and S. H. Strogatz (1998). "Collective dynamics of 'small-world' networks." Nature 393 (6684): 440-442.
White, H. C. (1970). Chains of Opportunity: System Models of Mobility in Organizations. Cambridge, MA. Harvard University Press.
White, H. C. (1970). "Search parameters for the small world problem." Social Forces 49 (2): 259-264.
White, H. C., S. A. Boorman and R. L. Breiger. (1976). "Social structure from multiple networks I: Blockmodels of roles and positions." American Journal of Sociology 81: 730-781.
Zachary, W. (1977). "An information flow model for conflict and fission in small groups." Journal of Anthropological Research 33: 452-473.
*Note
An earlier draft of this
paper was presented at the 28th International Sunbelt Network
Conference at St. Pete Beach, FL in January 2008. The author wishes to thank
his colleagues, Morry Sunshine, Ron Breiger, Elisa Bienenstock, Natasa Przulj,
Kim Romney and Russ Bernard for their helpful comments on this paper.
[1] Only recently (Hage and Harary, 1995) has the eccentricity of each node been defined as an index of its centrality and their definition was introduced in the literature of social network analysis.
[2] The notion of the degree of a node has recently been used in physics, but most of that use has involved degree distributions; it has not focused on degree as an index of the centrality of a node.