JoSS Article: Volume 6
Density or Distinction? The Roles of Data Structure and Group Detection Methods in Describing Adolescent Peer Groups
Scott D. Gest, gest@psu.edu
Pennsylvania State University [1]
James Moody, jmoody77@soc.duke.edu
Duke University
Kelly L. Rulison, klr250@psu.edu
Pennsylvania State University
Abstract: Despite cross-disciplinary interest in social influence among adolescent peer groups, significant variations in collecting and analyzing peer network data have not been explored, so it is difficult to disentangle substantive and methodological differences in peer influence studies. We analyze two types of network data (self-reported friendships and multi-informant reports of children who “hang around together a lot”) with three methods of identifying group structures (two graph theoretic approaches and principal components analysis) to explore substantive differences in results. We then link these differences back to underlying features of the networks, allowing greater insight into the general problem of identifying groups in network data. We find that different analytic approaches applied to the same network data produced moderately concordant group solutions, with higher concordances for multi-informant data. The same analytic approaches applied to different relational data (on the same nodes) produced weaker concordance, suggesting that the underlying data structure may be more salient than analytic approach in accounting for different results across studies. Behavioral similarity among group members was greatest for approaches that rest directly on density of direct ties.
I. Introduction
Sociological and psychological research on adolescent peer groups has often proceeded along parallel tracks, exploring similar phenomena but within distinct traditions for collecting and analyzing peer network data. Building upon a rich tradition of general social network analysis theory and methods (Doreian, Kapuscinski, Krackhardt, & Szczypula, 1996; Freeman, 2003; Friedkin & Cook, 1990; Moody, 2001a) sociologists have studied the structure of adolescent peer groups and their dynamic change over time (Doreian et al., 1996; Hallinan and Tuma, 1978; Hallinan, 1978; Haynie, 2001; Holland and Leinhardt, 1977; Moody, 2001b) as well as social influence and diffusion processes (Cohen, 1977; Giordano, Cernkovich, Groat, Pugh & Swinford, 1998; Jussim & Osgood, 1989). Similarly, psychologists have built upon theories emphasizing peers as contexts for individual development (Hartup, 1996; Kindermann, 1996; Sullivan, 1953) to study structure and change in dyadic and group networks (Berndt & Hoyle, 1985; Cairns, Leung, Buchanan & Cairns, 1995; Farmer, Estell, Bishop, O’Neal, & Cairns, 2003>; Urberg, Degirmencioglu, Tolson, & Halliday Scher, 1995) and the influence of peers on individual adaptation (Berndt, 1982, 1992; Cairns & Cairns, 1994; Hanish, Martin, Fabes, Leonard & Herzog, 2005; Kindermann, 1993).
Despite this parallel interest, there are relatively few cross-citations in the major sociological and developmental journals concerned with peer group processes. This is unfortunate because different data collection and analytic traditions have emerged in the two fields, making it difficult to integrate findings and slowing the transfer of insights and innovations from one field to the other. Our goal in this paper is to contribute to a productive integration of these traditions by using unique data from a single setting to explore the comparability of peer groups identified when two common adolescent peer network data collection procedures are analyzed with three common group identification algorithms.
In the peer context, data collection procedures typically vary along three dimensions: the substantive meaning of a social tie (friendship/affection vs. interaction), the level of analysis (dyad vs. group) and the informant (self-report vs. multi-informant). These three dimensions allow for many distinct measurement strategies, but for conceptual and practical reasons two measurement strategies have gained widespread use: self-reports of dyadic friendships and multi-informant reports of interaction-based groups. Similarly, while the number of grouping algorithms found in the literature is large, identifying principled axes of difference is more difficult. Two general approaches common in the literature are density-based graph-theoretic algorithms from the social network tradition and algorithms based on correlated patterns of social ties from the developmental studies tradition.
While others have studied a broader set of grouping algorithms (Freeman, 2003), we focus on these core disciplinary approaches to help foster comparability across a wide literature gap and to help link group comparisons directly to features of the network structure. Comparing grouping algorithms poses a difficult research design trap: if each approach is effectively maximizing its specific group-definition, one runs a clear risk of simply comparing incompatible definitions – that is, there is no clear external indicator of the true solution. However, in the absence of an external metric, being able to first compare different solutions then link those differences to underlying graph patterns helps flesh out the substantive meaning of otherwise implicit definitional differences embedded in grouping algorithms. In the adolescent peer group context explored here, we expect that differences in data type will affect the transitivity, density and structural cohesion (path structure) of the graph, and thereby lead to differences in how the three algorithms assign nodes to groups. Substantively, we hope these comparisons will provide a first step in establishing the degree to which studies of “peer networks” within different measurement and analysis traditions identify similar phenomena.
Approaches to Collecting Adolescent Peer Network Data
Self-reports of friendship dyads. Asking adolescents to name their friends is perhaps the most common measurement procedure in both sociology and psychology. Because friendships are typically defined as voluntary relationships based on liking, this procedure can be seen as a special case of defining meaningful social ties in terms of closeness, affection or liking, which has long roots in both sociological (Homans, 1950; Sampson, 1969) and developmental research (Bukowski, Newcomb and Hartup, 1996). Some researchers underscore this point by asking adolescents to name their “best” or “closest” friends or by asking adolescents to name classmates they like or feel close to. Developmental theorists have long held that feelings of friendship or closeness motivate attempts to understand and accommodate the friend’s concerns, thus providing one process of peer influence (Hartup, 1996; Newcomb and Bagwell, 1995; Sullivan, 1953). Because feelings of liking or affection are inherently subjective, self-reports are seen as the definitive method for identifying adolescents’ friendship preferences.
There is considerable variability both within and across disciplines in the way researchers analyze self-reports of friendships. Psychologists typically focus on friendship dyads and for theoretical reasons often restrict attention to reciprocated friendship choices (Berndt and Murphy, 2002; Hartup 1996), although some also consider non-reciprocated nominations (Hektner, August & Realmuto, 2000; Mrug, Hoza & Bukowski, 2004; Snyder, Horsch, & Childs, 1997) and larger group structures (Urberg et al., 1995). In contrast, sociologists often focus on group structures and typically look to asymmetries in nominations as indicators of group hierarchy and status, although some also remain focused on dyads (Hallinan and Tuma, 1978; Hallinan, 1978) or on reciprocated nominations (Coleman, 1961).
Multi-informant, interaction-based groups. A second measurement procedure that is increasingly being used in psychological research involves asking every adolescent in a social network to identify classmates who “hang around together a lot” (Cairns, Perrin and Cairns, 1985; Cairns, Cairns, Neckerman, Gest and Gariepy, 1988). As with self-reported friendships, this procedure embodies a particular perspective on the nature of social ties, the relevant level of analysis and the most suitable informant. Asking adolescents to identify peers who “hang around together a lot” means that social ties are defined in terms of interaction frequency. This makes sense from the perspective of social learning theories (Cairns, 1979; Patterson, 1974, 1982), which suggest that social behaviors are established, maintained and changed through repeated instances of modeling and reinforcement that occur within social interactions. For example, the quantity of preschool girls’ interactions with aggressive peers predicted increases over time in their own problem behavior (Hanish et al., 2005); and the quantity of delinquent adolescent boys’ friendship conversations that involved a well-organized focus on antisocial activities predicted the persistence of antisocial patterns (Dishion, Nelson, Winter, and Bullock, 2004).
The visible nature of social interactions suggests that reports may be obtained from any individuals with access to the relevant interaction settings. Certainly self-reports of interaction patterns are feasible and face-valid (Bagwell, Coie, Terry, and Lochman, 2000). Direct researcher observations can also be very effective with young children (Hanish et al., 2005; Ladd, 1983; Strayer & Santos, 1996; Vaughn and Waters, 1981), but are expensive to gather and have two disadvantages during adolescence: some important interaction settings may be inaccessible to researchers (e.g., hallways, buses), and those that are available (e.g., classrooms) may be misleading due to the strong constraints they impose on interaction patterns (Feld, 1981). In contrast, peers can be seen as expert participant-observers in the adolescent social network with unique access to a range of relevant settings. In a procedure developed by Cairns (described in detail below), all peers in a network are prompted to identify classmates who “hang around together a lot,” and the multiple reports are summarized in a symmetric “co-nomination matrix." The use of information from multiple informants to construct a global network was independently developed in the line of research on cognitive social structures (CSS; Krackhardt, 1987). The Cairns method differs from the CSS approach in that informants (“perceivers” in CSS terms) are not limited to reporting on common group membership, but rather are allowed to inform on any relation connecting others in the network.
Self-reports of friendship dyads and multi-informant reports of interaction-based groups are conceptually and operationally distinct ways of assessing adolescent peer networks. The two approaches differ in how they define the basis of social ties (closeness vs. interaction), the level of analysis at which data collection occurs (dyad vs. group) and the informant (self- vs. multi-informant). The resulting data structures are quite different: self-reports of friendships produce a directed adjacency matrix whereas multi-informant social groups produce a symmetric co-nomination matrix. These data differences often result in different degrees of density and transitivity. The group-basis of multiple-informant data results in graphs similar to the one-mode projection of two-mode graphs, with significantly more closed triads than self-reported graphs, which tend to be sparser. Each approach is a conceptually coherent strategy for identifying “adolescent peer groups”, but it is not at all obvious that groups derived from subjectively perceived, dyadic friendship ties are equivalent to those derived from consensually perceived, visible group interaction patterns. When researchers use these two different strategies to identify “peer groups”, are they studying the same thing?
Approaches to Identifying Group Structures
Similarities in patterns of ties. There is a long tradition of grouping together individuals who share similar patterns of social ties. Early social network researchers used principal components analysis or centroid factor analysis to identify groups (factors) from interaction (e.g. Wright and Evitts, 1961) and nomination matrices (e.g., Bock and Husain, 1952; MacRae, 1960). More recently, a growing number of developmental researchers have used correlation-based algorithms to identify peer groups from multi-informant reports (Boivin & Hymel, 1997; Cairns et al., 1985, 1988; Estell, Cairns, Farmer & Cairns, 2002; Farmer et al., 2003; Rodkin, Farmer, Pearl, & Van Acker, 2000; Xie, Cairns & Cairns, 1999). One group has used principal axis factoring to identify groups from an adjacency matrix (Bagwell et al., 2000). Principal components analysis (PCA) has also been applied to co-nomination matrices (Gest, Rulison and Welsh, 2005). These approaches share the premise that groups can be conceptualized as individuals whose patterns of received friendship nominations or whose profile of co-nominations with peers are similar (i.e., correlated). These approaches have clear links to the block-modeling traditions rooted in CONCOR (White, Boorman, and Breiger, 1976), where actors are classified as similar if they have similar nomination patterns to/from others in the network. One of the potential advantages of the PCA approach, as will become evident below, is that an element of structural equivalence informs the construction of primary groups, allowing one to identify groups that are both internally dense and similarly situated in the graph at large.
Direct approaches. The social network field has identified many approaches for finding primary groups in networks (Frank, 1995; Fershtman, 1997; Burt, 1978; Freeman, 1992; Richards, 1995; Seidman and Foster, 1978). A basic division in such methods is between those that identify exact graph theory features and those that search the graph to identify a solution iteratively. Many graph-theoretic methods for finding primary groups are challenged in settings where data are messy, resulting in assignments that are not robust to the kinds of data that analysts typically encounter (see Moody, 2001a for a review). These methods also often identify groups that heavily overlap. Recent work on structural cohesion has taken this feature as a strength of the model, in that k-connected components have a strictly defined and interpretable overlap structure and are more robust to data quality as k-cohesion increases.[2]
The alternative approach has been to identify groups based on a search and clustering process, using algorithms that attempt to generate clusters with relatively high in-group density. The exact algorithms vary significantly. One line of work makes many assignments of nodes to groups in attempts to minimize a cost function (Borgatti, Everett, and Freeman, 1999; Guimera and Amaral, 2005). Much of the research on group detection algorithms has been to identify ways to seed or speed these types of searches, with some very sophisticated pattern recognition approaches being most popular (Richards, 1995; Fershtman, 1997). While often successful in small groups, these iterative solutions can be very time-consuming on large networks. Recent work has attempted to identify search processes either directly on graphs, such as extensions of simulated annealing processes (Guimera and Amaral, 2005) or on summary statistics generated by the network structure (Moody, 2001a) that allow searches of very large networks. Finally, a third line of research has taken a statistical modeling approach, using guided search algorithms based on a tie probability model (Frank, 1995). These models work on the logic that groups should focus on ties, so the probability of a tie between i and j (pij) is a function of a parameter on the group partition, and nodes are juggled across partitions until that parameter is maximized.
The Present Study
To our knowledge, within the literature on adolescent peer social networks, there are no empirical reports comparing the group solutions obtained when factor-analytic and graph-theoretic grouping algorithms are applied to two of the most common types of peer network data. To begin linking these different data collection and analytic traditions, we use a single data set to identify adolescent peer groups based on two types of peer network data (self-reported friendships and multi-informant interaction-based groups) with each of three group identification methods (principal components analysis and two graph-theoretic algorithms).
II. Methods
Participants
Data were provided by 134 (62 girls, 72 boys) of the 150 students (89%) enrolled in the 6th grade at a middle school serving a small, working-class community in central Pennsylvania. This data permitted us to describe the peer networks of 148 (68 girls, 80 boys) of the 150 students (see below). Students at the school scored near the statewide average on tests of achievement, although rates of poverty in the community exceeded the state average. Almost all students (99%) were Caucasian, reflecting the demographics of the community. This project was a component of a Safe Schools / Healthy Students grant obtained by the school district from the U. S. Departments of Education, Justice and Health and Human Services. Prior to the October student survey, parents were mailed letters describing the project with a form to sign if they did not wish their child to participate. Students whose parents did not return a form exempting them from the project were asked to complete a group-administered survey lasting approximately 45 minutes. Students were free to decline to participate in the survey.
Peer Network Data
Self-reported friendships. We construct friendship groups from students’ reports of friendships. Students were asked: “Some kids have a lot of friends, some kids have one friend and some kids don’t have a friend. What about you? List the names of any friends you have in your grade.” Students were provided a roster containing the names of all students in the 6th grade, organized by homeroom. Space was provided for students to list up to ten names, although some students listed several more than that (range: 0 to 31 nominations). These data were organized into an adjacency matrix. For the principal component analyses, we entered ones along the diagonal (MacRae, 1960).
Multi-informant groups. We construct multi-informant groups using Cairns’ Social-Cognitive Map (SCM) method. Students were asked: “Are there some kids in your grade who hang around together a lot? List the names of the kids in each of the different groups in your grade. Try to think of as many groups as you can.” Space was provided for students to list up to nine groups with up to ten individuals per group and students were free to list themselves in a group. Two observational studies confirm that the frequency of being named to the same group is correlated with observable interaction rates (Cairns et al., 1985; Gest, Farmer, Cairns & Xie, 2003). For example, 4th and 7th grade students interacted with members of their multi-informant groups at rates three to four times higher than with other same-sex peers (Gest et al., 2003). In the present study, all nominations were organized into a symmetric co-nomination matrix in which off-diagonal cells indicated the total number of times two individuals were named to the same group. Values along the diagonal indicated the total number of times a given child was named to any social group. Students were not required to classify all peers into groups, so there was variability in how often different adolescents were named to groups.
Social behavior, educational attitudes and achievement. We examine group homogeneity with respect to four measures of social behavior and educational attitudes and achievement. Following standard procedures in the developmental literature on peer relations (Coie, Dodge & Copotelli, 1982), we asked each adolescent to name the peers s/he liked the most and the peers s/he liked the least. The number of times each adolescent was named as liked most and least was tallied and standardized within gender. The difference between each adolescent’s standardized liked-most and standardized liked-least scores was computed as an index of peer social preference, and this score itself was standardized within gender (M = 0, SD = 1, Skew = .04). Aggression was measured with five items rated by teachers on a 5-point scale (a= .92; 1 = low, 5 = high). To better capture the highly skewed scores on aggression, each child was classified as non-aggressive (76.6% of sample with Mean scores <2.0 on the 5-point scale), Moderately Aggressive (14.6% with Mean scores between 2 and 3) or Highly Aggressive (8.8% with Mean scores greater than 3.0). Liking for school was measured with a single item measured on a 5-point Likert scale (“I like going to school”; M = 3.31, SD = 1.32, Skew = -.29). Grade Point Average (GPA) was calculated as the average of students’ grades in Reading, Social Studies, Math and Science during the 1st grading period (M = 3.40, SD = .66, Skew = -1.01).
Principal Components Analysis (PCA)
We applied principal component analysis to both types of peer network data. First, we extracted all factors[3] that had eigenvalues greater than 1.0, resulting in 39 factors for the self-reported friendship data and 38 factors for the multi-informant network data. Factors with eigenvalues less than 1 were not extracted because these factors explain less variance in the solution than a single variable. Second, we applied a Varimax rotation and then determined whether each factor was defined by at least three individuals whose primary loading (>.30) was on that factor. We required three individuals per factor because the theoretical definition of a group requires at least three members and we required factor loadings above .30 to ensure that each individual shared at least 9% of their variance with the group.[4] When one or more factors did not meet these criteria, we re-ran the PCA extracting one less factor, resulting in 24-factor (group) solutions for both types of network data. This process, along with using Varimax rotation, allowed us to obtain maximum differentiation while still identifying empirically reliable and conceptually meaningful groups. Some adolescents had significant factor loadings on more than one factor that could be interpreted as reflecting membership in more than one group, but for purposes of comparing grouping solutions across methods, we assigned such “dual-members” to the group on which they had the highest loading.
Graph-Theoretic Techniques
We use two social-network based group detection methods to compare with the PCA routine: Moody’s (2001a) Recursive Neighborhood Means (RNM) approach and UCINET VI’s FACTIONS (FAC) routine (Borgatti et al., 1999). The RNM approach was chosen because of its theoretical link to the substantive problems of peer effects and the FAC routine because it is commonly available and thus likely to be used by others. Like the PCA routine, both of these approaches are “indirect,” in that they do not search for a particular graph theoretic pattern (like cliques), but instead use the observed network to generate a cost / similarity score that is clustered or maximized. These types of indirect routines are useful, as many of the direct graph theoretic approaches (such as searching for cliques or k-cores) are either very slow algorithmically or have substantive difficulties identifying primary groups.
Moody’s RNM routine was originally designed as an efficient means to cluster very large (>10,000 node) networks, but its theoretical foundation in peer influence models (Friedkin, 1998; Friedkin and Cook, 1990) suggests that it should be substantively useful for settings where peer influence is the central concern. The RNM routine uses a two-step procedure. In the first step, one simulates a peer influence process on k random variables. The peer influence simulation then adjusts each person’s score on each random variable to equal the (tie-strength weighted) mean of the people to whom they are connected. Because the original variables are uncorrelated, dense clusters of nodes will come to occupy unique positions in the k-dimensional space defined by the resulting distribution of random variables. In the second step, one uses cluster analysis (here we use Ward’s minimum variance method) to identify groups based on the resulting influence variables. The number of groups is determined by examining changes in fit statistics (here we used Freeman’s (1972) segregation index as our guide), such that two initially distinct groups are joined if doing so significantly improves the fit for both groups. In addition, any small or disconnected groups were examined manually to see if nodes would be better classified by placing these nodes in a “between” group position.[5]
The FAC routine searches for groups with a “clique-like” structure. A perfectly clique-like structure would have groups that are completely connected internally (everyone tied to everyone else) and no ties outside of the groups. Thus, the routine counts null dyads within groups and ties outside of groups as deviations from the ideal, and adjusts group boundaries to minimize the number of such deviations. As with many of the group detection algorithms, one must determine the number of factions initially. Initial examinations of these data showed that the RNM approach was finding fewer groups than the PCA approach, so we choose 20 groups as a number that “split the difference” between the other two approaches.
For both the RNM and the FAC routines, we treated the data as symmetric, but weighted reciprocated ties more than asymmetric ties.[6] For the multi-informant nomination data, we used the number of times each pair was nominated as being in the same group as the basis for the tie weight. Initial FAC runs suggested that the predominance of often non-concordant single naming was throwing the results, so we limited analysis to pairs with 2 or more co-nominations.
Comparing Alternative Results
Part of the difficulty in finding primary groups in networks is defining exactly what features represent a primary group. While theoretical and algorithm advances have been made in identifying particular aspects of network structure that clarify our understanding of primary groups [such as structural cohesion (Moody and White, 2003), tie strength (Freeman, 1992), clustering and distance ( Holland and Leinhardt, 1970; Holland and Leinhardt, 1971; Watts, 1999) and the ratio of in-group to out-group ties (Fershtman, 1997; Guimera and Amaral, 2005)], there is no unified agreement on what counts as a “clique-like” subgroup. In the substantive setting of interest here, we expect primary peer groups to be small and tight-knit. In general, we also expect them to be largely distinct,[7] with relations / interaction falling disproportionately within the primary group. We use six measures to examine how “tight-knit” and distinct the group solutions are for both types of data.
Tight-knit primary groups are likely to be relatively dense and have many closed triads that hold the local group together. In general, network density is the average value of relations taken over all possible dyads. We measure relative density as the density of ties falling within group divided by the density of ties that fall outside of groups. To account for group structure as well as volume (Freeman, 1992), we use two triad-based measures. Closed triads capture cases where friends of friends are friends (transitive relations), and we expect substantively that primary friendship groups will be characterized by relatively high numbers of closed triads. The transitivity ratio is defined as the proportion of all potentially closed triads that are actually closed. It is calculated as the proportion of all two-step paths (iàj, jàk) that are also direct paths (iàk). We define the relative transitivity ratio as the transitivity ratio calculated only among within-group dyads over the transitivity ratio of the entire network. Ideally, groups should enclose closed triads, thus any case of a group boundary separating a closed triad is a deviation from the ideal-type model. We thus measure the proportion of all closed triads (T300) that fall entirely within group to capture how often group solutions encapsulate closed triads.[8]
The distinctiveness of a group is measured by how often relations fall within rather than between groups. We use Freeman’s segregation index (1972), the proportion of all ties that fall outside of groups, and the modularity index (Newman and Girvan, 2004) as three measures of group distinction. Freeman reasoned that if a group partition was irrelevant, then relations should be distributed randomly across the group boundaries. Freeman’s network segregation index is thus calculated as the difference between the number of observed cross-group ties and the number of randomly expected cross-group ties, divided by the number of randomly expected cross-group ties. When the value is 1.0, all relations fall within separate groups. When the value is 0, then relations are distributed randomly across groups. The modularity statistic (Newman and Girvan, 2004) follows a similar logic and will be 0 if ties are distributed randomly. The advantage of the modularity score is that the measure reaches a clear maximum value when ties are more likely to fall within groups, making it ideal for comparing group distinctiveness across solutions. Finally, the proportion of ties that fall outside of groups provides a readily interpretable (though not gauged against random chance) metric for the sheer volume of cross-group ties.
Group size enters into our consideration both substantively and methodologically. Substantively, children’s primary groups tend to be small (Rubin, Bukowski and Parker, 1998) and thus any solution that generates very large groups lacks a certain level of face validity. However, we also expect a group to have a certain extra-individual character that extends beyond any single individual member (Simmel, 1950; Moody and White, 2003). The smallest collection that can exist independent of any single actor is the triad, and thus groups are typically defined as having 3 or more nodes. Methodologically, the distribution of group sizes affects all of the other metrics used to define groups. On the one hand, if all nodes were partitioned into a single group, then there would be no out-of-group ties and all triads would fall within the group (there would, of course, be no data reduction here either!). On the other hand, if everyone were assigned to a single closed triad, then in-group density would be perfect, leading to very high relative densities and relative transitivity ratios.[9] Finally, we use two versions of the Rand statistic (Rand, 1971) to compare the different primary group solutions statistically and “Shadow plots” (Batagelj and Mrvar, 2001) to evaluate overlap qualitatively. Measures for comparing nominal distributions, such as Kappa, are ineffectual if the number of groups differs across solutions. The Rand statistic, in contrast, allows us to compare clustering solutions with any number of clusters. Substantively, the Rand statistic measures the proportion of pairs classified similarly in two solutions. A pair is similarly classified if they were put in the same cluster in both solutions, or classified as being in different clusters in both solutions. A value of 1.0 means that the two partitions are substantively identical. While intuitive, the raw Rand statistic does not distinguish observed matching from matching expected by chance. Since each pair has to be placed in some cluster, a proportion of pairs will be similarly classified due simply to chance alone. We use the adjusted Rand statistic proposed by Morey and Agresti (1984) to correct for chance overlap. This measure captures the percent difference from chance in the likelihood that a pair of actors is similarly classified. Shadow plots are schematic images of an adjacency matrix, with the rows and columns sorted to help see the structure in the graph. Cell values are shaded (“shadowed”) proportional to the strength of the ij cell, and allow us to visually compare the overlap of the group solutions to the underlying tie-distribution.Analytic Strategy
The analysis progresses in three stages. First, we provide descriptive information about the friendship and multi-informant data: the number of friends and groups identified, tie density and transitivity, sociograms, and a regression model clarifying the correspondence between multi-informant group nominations and friendship nominations. Second, we quantify the agreement among the various group solutions using the adjusted Rand index. Third, we examine differences in the structural features of the groups identified from the multi-informant and self-reported friendship data, with a special focus on reasons for lower concordance across analytic strategies in the case of self-reported friendship data.III. Results
Descriptive Summary of Peer Network Data
Reports of friends and groups. On average, adolescents listed 9.72 friends (SD = 3.95) and identified 3.76 groups (SD = 2.01) with 4.60 (SD = 2.10) individuals per group (i.e., a total of 17.26 group members). More than half of all self-reported friends (59.4%) and more than half of all peers nominated to social groups (51.1%) were outside of the adolescent’s own homeroom, confirming that the social network is appropriately considered at the level of the entire grade.
Graph statistics. The multi-informant group data demonstrated a high density of ties (.486) and transitivity (.571). This suggests ample “clusteredness” to be exploited by each grouping method, which is to be expected, since the data generates ties between all pairs named as members of the same group. In contrast, the self-reported friendship data had lower density (.121) and transitivity (.302) scores. This will make finding groups consistently more challenging than with the multi-informant data, because there will be less clustering for the algorithms to exploit.
Sociograms. Next we constructed sociograms illustrating each type of network data. In each sociogram, position in the xy plane is determined by a force-directed automatic layout algorithm implemented in PAJEK (Batagelj and Mrvar, 2001). For these layouts, social ties are analogous to springs, with stronger values indicating a stronger pull between the nodes. As such, two nodes that are connected will tend to be close to each other, while nodes that are disconnected will be further apart. In an ideal-typical sense, if the network were composed of very distinct groups (and the nominations reflected these groups), then the figure would contain distinct “clumps” for each group.
Figure 1. Self-reported Friendship Nominations
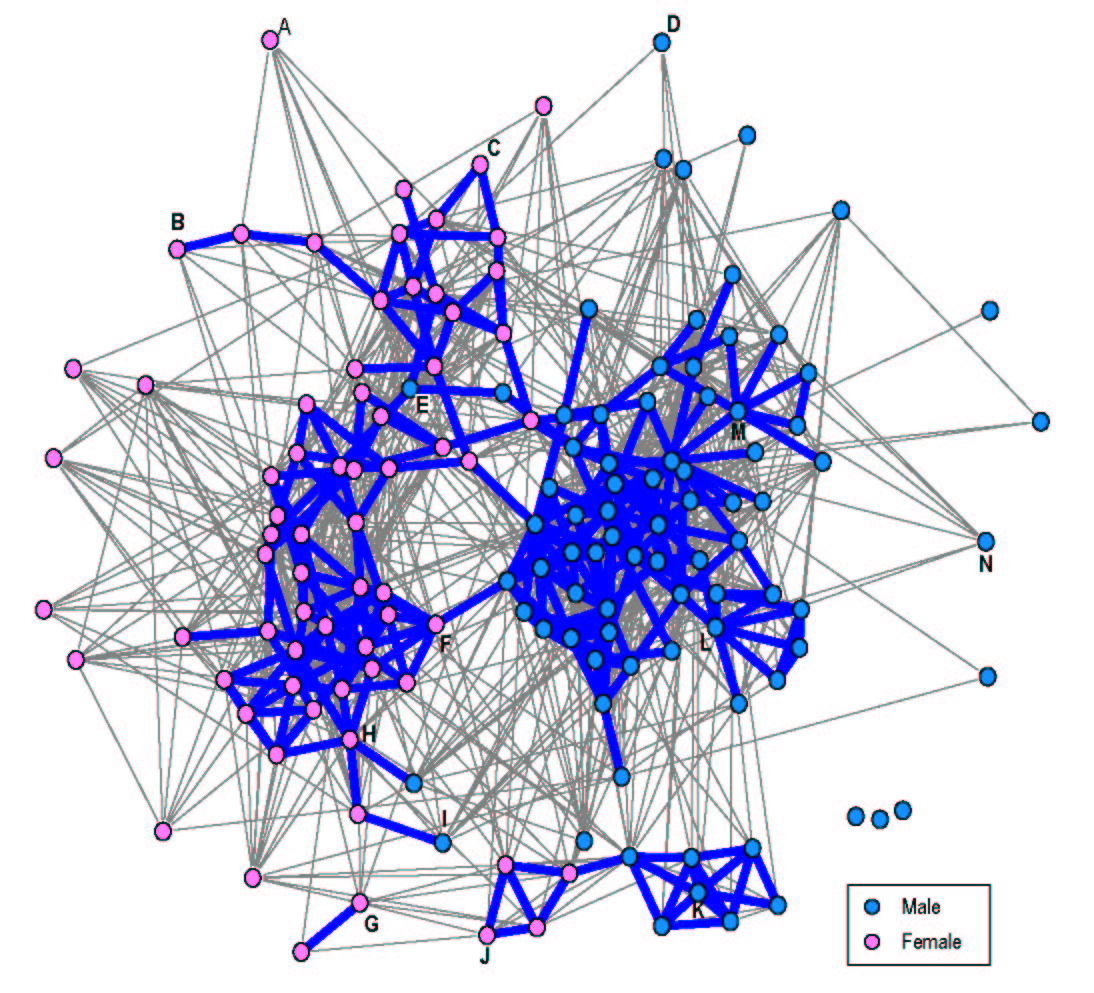
Thick Blue lines are reciprocated friendship nominations, thin gray are asymmetric nominations. Letters identify particular nodes to compare with Figure 2.
In Figure 1, each node represents a student and each line represents a friendship nomination. For the present analyses, asymmetric ties (thinner lines) count less than symmetric ties (thicker lines). This figure shows that friendship nominations among 6th graders are heavily conditioned by sex. Beyond this strong sex segregation, the network does not suggest many small groups, particularly among the males. Instead, both the male and female sides of the network have a “core-periphery” structure, with a small number of individuals who have no reciprocated ties, and a large cluster of individuals who are strongly connected. Females in the network are slightly more differentiated, with what appears to be two or three overlapping “clumps” stretching along the “north-south” axis. In addition, there are two small groups in the “south-east” portion of the figure with no reciprocated connections to the rest of the network, but one link between them. These were students who spent part of their day in a Special Education classroom: despite being “mainstreamed” in General Education classrooms for much of the school day, these children’s friendships were largely separate from the rest of the grade.
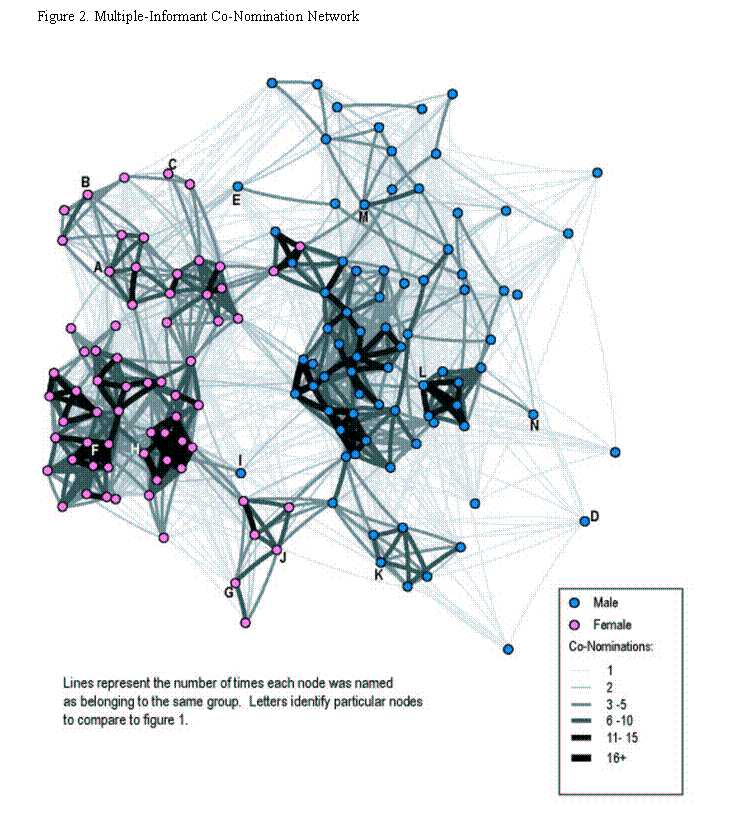
In Figure 2, each line indicates the number of times that two students (nodes) were named as being members of the same group. The thickness and shade of the line corresponds to the frequency of co-nomination to the same group. Although the number of co-nominations linking individual nodes ranged from 1 to 33, for clarity these values were grouped into six ranges. There are three immediate impressions given by this figure. First, there are clear clusters with very strong agreement (thick lines), particularly among the females, indicating substantial consensus among students regarding the interaction patterns of their peers. Second, there are large individual differences in the maximum number of co-nominations linking a given student to other students: the maximum number of co-nominations is centered around 10 (Mean = 11.1, Median = 9.0), but 39 (27.1%) students were never named more than 5 times with any peer, while 18 (12.5%) students reached over 20 co-nominations with at least one of their peers. Third, the wide linkages at low levels (the very thin lines connecting a wide body of nodes across the graph) suggests that some people provide idiosyncratic reports of groups that are at odds with the group consensus.
In general, the two sociograms correspond quite closely in terms of the overall shape, the separation of males and females, and the location of individual nodes (fourteen of which are labeled, A through N, on each graph).[10] The two groups of special education students in the southern portion of the graph (including nodes G, J and K), for example, contain nearly identical members. In addition, 3 of the 4 male nodes in the “female” section of the friendship graph (including nodes E and I) are similarly more closely associated with the female side of the multi-informant graph. In both graphs, boys L and M occupy similar positions in clusters outside the main clump of boys, while girls H-F and B-C are located in parallel positions within the relatively core groups of girls. Boys N and D reside on the periphery of both graphs, whereas girl A is peripheral in the friendship graph but closer to the core of the multi-informant graph.
Correspondence between friendship and multi-informant nominations. We tested the degree to which the number of times two people were nominated as hanging out together predicted friendship nominations. We model the likelihood of a friendship nomination, controlling for network and group involvement measures including: number of friends named, number of friendship nominations received, number of group nominations received and the sex composition of the dyad. Because the dependent variable is dichotomous (nominated or not), we use a logistic regression model. The results (Table 1) clearly show that the number of times a dyad is nominated to the same group strongly predicts a friendship nomination.
Table 1. Logistic Regression of Friendship Nomination on Multi-informant Co-nominations (odds ratio in parentheses)
|
Variable |
Model 1 |
Model 2 |
Model 3 |
Model 4 |
|
Intercept |
-4.87 |
-6.31 |
-6.54 |
-6.28 |
|
# of friends named by ego (ODG) |
0.138 (1.15) |
0.145 (1.16) |
0.144 (1.16) |
0.145 (1.16) |
|
# of times alter was named as a friend (IDG) |
0.146 (1.16) |
0.144 (1.16) |
0.144 (1.16) |
0.153 (1.17) |
|
# of times ego named as a group member (ego visibility) |
-0.015 (0.989) |
-0.011 (0.989) |
-0.01 (0.989) |
-0.01 (0.989) |
|
# of times alter named as a group member (alter visibility) |
-0.008 (0.992) |
-0.008 (0.992) |
-0.007 (0.993) |
-.009 (0.991) |
|
Same sex dyad |
|
1.84 (6.355) |
2.05 (7.76) |
|
|
Both Male |
|
|
|
1.74 (5.71) |
|
Both Female |
|
|
|
2.04 (7.69) |
| Number of Co-Nominations |
0.603 (1.83) |
0.508 (1.66) |
1.09 (2.99) |
0.506 (1.66) |
|
Group x Same Sex |
|
|
-0.610 (0.544) |
|
|
|
|
|
|
|
|
Pseudo R2 |
0.37 |
0.423 |
0.428 |
0.424 |
Note. All variables are statistically significant at the .0001 level.
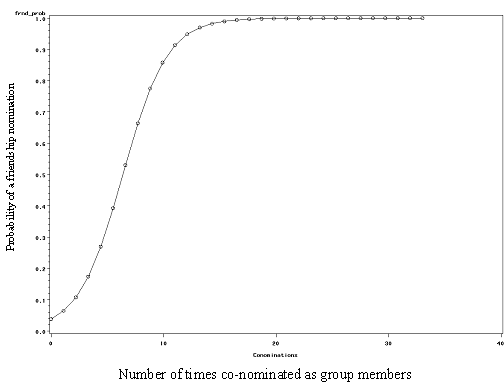
After controlling for sex composition of the dyad, the odds of a friendship nomination increase by 1.66 for each time the pair is said to belong to the same group. This effect differs by gender composition. Specifically, a co-nomination is more likely to predict a friendship when the dyad is cross-sex, though the relative rarity of these nominations makes this finding somewhat less important. As expected, the controls for network expansiveness (ODG) and attractiveness (IDG) are also important. While statistically significant, simple visibility of either party really does not matter that much (the odds ratios are close to 1.0). To simplify the interpretation of this coefficient, Figure 3 plots the predicted probability of a friendship nomination for a same-sex dyad, by the number of times they are nominated as being in the same group (estimates based on model 2).[11] This figure indicates that (in these data) the likelihood of a self-reported friendship reaches 50% as the number of multi-informant interaction co-nominations reaches around 7, and exceeds 95% when the number of co-nominations reaches around 13.
Comparability of Group Solutions
Table 2. Comparability of Group Solutions|
|
|
Self Nominations |
Multi-Informant Nominations |
||||
|
|
|
RNM |
FAC |
PCA |
RNM |
FAC |
PCA |
|
Self Nom |
RNM |
--- |
0.328 |
0.362 |
0.417 |
0.392 |
0.316 |
|
FAC |
0.861 |
--- |
0.475 |
0.464 |
0.498 |
0.465 |
|
|
PCA |
0.873 |
0.949 |
--- |
0.584 |
0.572 |
0.465 |
|
|
Mult Nom |
RNM |
0.881 |
0.942 |
0.958 |
--- |
0.687 |
0.695 |
|
FAC |
0.872 |
0.947 |
0.957 |
0.965 |
--- |
0.665 |
|
|
PCA |
0.862 |
0.948 |
0.948 |
0.969 |
0.966 |
--- |
|
Note. Values above the diagonal are the chance-adjusted Rand statistic (Morey and Agresti, 1984). Values below the diagonal are the simple Rand statistic, unadjusted for chance. The interpretation of the Rand statistic is the probability that a randomly chosen pair will be similarly classified by the two partitions. The interpretation for the adjusted Rand is the percent difference between the number of observed agreements and the number of chance agreements.
We next examined the similarities between grouping algorithms for both types of data. Table 2 contains the Rand matching coefficients describing the comparability of the node partitions across the six different combinations of network data and group identification algorithm. The positive coefficients across all comparisons indicate that the partitions are significantly correlated, but the differences that occur are systematic. Overall agreement is higher across the three multi-informant solutions (mean Rand=0.97, Adjusted Rand=0.68) than across the three self-reported friendship solutions (mean R=0.89; AR=0.39). This main effect of network data is quite large, and due largely to the clear clustering evident in the multi-informant matrix. Effectively, subgroups in the multi-informant network are much easier targets to hit than in the less clustered friendship network, so that differences in grouping algorithms are less likely to lead to divergent grouping solutions.
Within the friendship network, the RNM solution is less similar to the other two (AR: RNM,FAC =0.33; RNM,PCA =0.36) than they are to each other (FAC,PCA =0.48). This suggests that the three methods differ in their basic strategies which, as we will see below, trade off larger, distinctive groupings (RNM) and smaller groupings with greater in-group density (FAC, PCA). Overall, the groups derived from the self-reported friendship data with a particular algorithm were as similar to groups derived from the multi-informant data (upper right quadrant of Table 2; median AR=.47) as they were to each other (AR range .33 to .48).
From the perspective of comparing results across different combinations of data collection techniques and analytic strategies, these results send a mixed signal. On the one hand, the significant chance-adjusted agreement across all six solutions indicates that investigators using a wide range of methods (measures*algorithms) are indeed describing similar phenomena. On the other hand, compared to self-reported friendship data, the more clustered multi-informant data produce much more consistent groupings across several analytic methods. We next turn to the details of the kinds of groups identified by each approach.
Differences in the Structural Features of Group Solutions
Table 3. Structural Features of Groups|
Type of Network Data |
Group Identification Procedure |
|||
|
Recursive Neighborhood Means |
FAC |
Principal Components Analysis |
Gender x Homeroom |
|
|
Self-Reported Friendships Density = .12 Transitivity Ratio = .57 |
|
|
|
|
|
# of Groups |
10 + 14 between |
20* |
24 + 3 unclassified |
|
|
Size: M (SD) |
13.3 (11.6) |
7.3 (1.9) |
6.04 (2.22) |
|
|
Min - Max |
5 - 43 |
5 - 12 |
3 – 12 |
|
|
Groups of size = 3 |
0 |
0 |
3 |
|
|
Relative Density |
9.76 |
11.43 |
13.61 |
7.84 |
|
Relative Transitivity |
1.58 |
2.56 |
2.60 |
2.14 |
|
Prop. closed triads in same group |
0.60 |
0.27 |
0.24 |
0.21 |
|
Freeman Segregation |
0.57 |
0.32 |
0.33 |
0.311 |
|
Modularity |
0.46 |
0.30 |
0.31 |
0.41 |
|
Proportion of ties out-of-group |
0.346 |
0.641 |
0.636 |
0.636 |
|
|
|
|
|
|
|
Multi-informant Groups Density .49 Transitivity Ratio = .57 |
|
|
|
|
|
# of Groups |
20+9 between |
20* |
24 + 1 unclassified |
|
|
Size: M (SD) |
6.95 (3.03) |
7.4 (2.6) |
6.13 (2.44) |
|
|
Min - Max |
4 – 14 |
5 – 13 |
3 – 11 |
|
|
Groups of size = 3 |
0 |
0 |
4 |
|
|
Relative Density |
27.22 |
30.83 |
29.72 |
10.87 |
|
Relative Transitivity |
1.54 |
1.66 |
1.67 |
1.54 |
|
Prop. closed triads in same group |
0.41 |
0.52 |
0.31 |
0.21 |
|
Freeman Segregation |
0.56 |
0.58 |
0.53 |
0.394 |
|
Modularity |
0.52 |
0.53 |
0.50 |
0.36 |
|
Proportion of ties out-of-group |
0.399 |
0.383 |
0.439 |
0.556 |
* Number of groups is definitional
Table 4. Within-Group Behavioral Homogeneity
|
|
|
|
Type of Network Data |
|
|
|
|
Group structure Index |
Self-Reported Friendships |
Multi-Informant Groups |
|
Group Identification Procedure |
Recursive Neighborhood Means |
Like Going to School |
.080 / .066 a |
.228 |
|
Peer Social Preference |
.142 / .143 |
.281** |
||
|
Teacher-rated Aggression |
.048 / .088 |
.204 |
||
|
Grade Point Average |
.080 / .226* |
.224 |
||
|
FAC |
Like Going to School |
.126 |
.220 |
|
|
Peer Social Preference |
.197 |
.342*** |
||
|
Teacher-rated Aggression |
.171 |
.229* |
||
|
Grade Point Average |
.247+ |
.246* |
||
|
Principal Components Analysis |
Like Going to School |
.235 |
.276* |
|
|
Peer Social Preference |
.366*** |
.317** |
||
|
Teacher-rated Aggression |
.403*** |
.439*** |
||
|
Grade Point Average |
.332** |
.289* |
||
* p < .05. ** p < .01. *** p < .001.
Note. Effects of group membership (Partial eta-squared) after controlling for gender. For the RCN self-reported friendship solution, values after the slash are the partial eta-squared values after removing group 1.
Table 3 contains the group structure statistics for the six clustering solutions and, for comparison, the statistics for a simple attribute clustering based on sex and homeroom. Table 4 contains estimates of group behavioral homogeneity. Below we briefly summarize results for the multi-informant networks before examining reasons for the variability in solutions for the friendship data.
Multi-informant Group Structures. The three methods produced similarly sized groups from the multi-informant data. The average group sizes were very similar for RNM and FAC (6.95 vs. 7.40) with a similar distribution of group size (range 4 to 14 for RNM; 5 to 13 for FAC), and PCA groups were only somewhat smaller (M = 6.13, range 3 to 11). Group tight-knittedness was very similar across solutions, with the relative density of in-group to out-group ties roughly three times higher for the RNM, FAC and PCA solutions (27.22, 30.83, 29.72) than for a partition reflecting the split by gender and homeroom (10.87). Group differentiation was also similar across solutions.
The estimates of group behavioral homogeneity were generally reliable and moderate in magnitude for each solution. Given the similarity in the partitions, it was surprising that homogeneity was consistently higher for the PCA groups than for the RNM groups, with homogeneity of FAC groups at intermediate levels. The substantially higher levels of similarity in aggressive behavior for the PCA groups was due largely to a subset of 13 boys, 5 of whom were highly aggressive (representing nearly half of the highly aggressive students in the entire grade). RNM and FAC placed all 13 individuals in the same group, whereas PCA separated them into a group of 8 that contained all 5 highly aggressive individuals and a group of 5 non-aggressive boys. The most likely explanation for the modest differences in similarity for the other behaviors is that PCA produced slightly smaller groupings, but we examine this issue more fully in the context of the friendship network solutions, which differed more substantially in additional ways. At this stage, the most noteworthy feature of multi-informant data was that three distinct group identification procedures produced solutions that were highly comparable in terms of structural characteristics, the placement of individuals into groups, and estimates of behavioral homogeneity.
Self-Reported Friendship Group Structures
Size. As with the multi-informant network data, the RNM and FACTION solutions tended to produce larger friendship groups than the PCA solution. FAC and PCA produced group sizes that were very similar to those obtained when the comparable method was applied to the multi-informant data (FAC: M = 7.3 for friendship data, M = 7.4 for multi-informant data; PCA: M = 6.0 and M = 6.1, respectively). The RNM friendship solution generated one male group of 43 nodes. This large cluster dominates the RNM solution, and appears to drive a number of the differences reported in the group structure below. When this group is excluded from consideration, the RNM solution for friendship data produces groups only a bit larger than those for multi-informant data (M = 8.5 vs. M = 6.95).
Internal density. The PCA solution produced groups with the highest density and internal transitivity, with the FAC groups being quite similar. More specifically, the relative density of ties for the PCA, FAC and RNM groups was 13.6, 11.4 and 9.8, respectively, and the within-group transitivity ratio for each was 2.60, 2.56 and 1.58. Again, much of the difference in this “tight-knittedness” for the RNM solution is attributable to the large group of 43 nodes. When that group is excluded, indicators of internal density are more similar for the remaining RNM groups.
Differentiation. The RNM groups were more highly differentiated than the PCA or FAC groups. Sixty percent of closed triads fall within RNM groups, whereas the majority of closed triads in both the PCA and FAC routines cross group boundaries, suggesting that the RNM solution effectively constructs groups so as to have relatively fewer contacts with other groups. This is evident in the other group clustering statistics as well. The segregation index for the RNM solution is 0.56, compared to 0.32 and 0.33 for the FAC and PCA solutions, respectively and the modularity score for RNM is 0.456, compared to 0.299 and 0.311 for FAC and PCA, respectively. Similarly, while 64% of ties fall outside of the FAC and PCA groups, only 35% of ties fall outside of RNM groups.
Behavioral homogeneity. The three solutions produced varying estimates of behavioral homogeneity. The ordering of these differences was the same as for the multi-informant data: PCA produced the largest estimates of homogeneity, FAC produced intermediate, but often statistically insignificant estimates, and RNM produced weaker and usually statistically insignificant estimates, which increased only modestly when the large group comprised of 43 individuals was excluded. Within methods, PCA-based estimates of homogeneity were comparable for the friendship and multi-informant data, but for both FAC and (especially) RNM, estimates of homogeneity were distinctly higher for the multi-informant data.
Summary. The less clustered self-reported friendship data produced results that varied more across analytic method than did the multi-informant data. In these circumstances, the RNM procedure achieves its relative advantage in differentiation at the cost of less tight-knit groups. That is, it appears that the RNM procedure tends to favor distinct groups, even if they are less internally dense, while the PCA and FAC solutions return groups that are internally very dense and transitive, but that also have many ties and closed triads falling outside of the respective groups. These differences were correlated with estimates of behavior homogeneity.
A Closer Look
What accounts for the differences in partition results for the self-reported friendship data? Figure 4 below provides an intuitive comparison of the RNM and PCA solutions.[12] Panel A presents the shadow plots for the overlap in assignments (1st matrix) and the raw data used to generate the cluster solutions (2nd matrix). The high-level of agreement for the multi-informant data is evident by the fact that most of the shaded cells in the first column are black – indicating that the pair was classified in the same group by both solutions. The matrix has been permuted to pull clusters along the diagonal. The places where the algorithms miss each other are colored gray (the pair was grouped together by one algorithm but not the other). You can see that when the algorithms “missed” they tended to be in very similar regions of the graph. For example, the largest amount of mismatch between the two solutions occurred in the block-diagonal cell in the lower right of this image, where both agreed on the pairwise placement of two smaller sections, but disagree on the remainder of the pairs. If we look at the corresponding region of the raw data, we see that this section had very high levels of joint nominations. The tendency for PCA to pick up dense rather than distinct groups accounts for the difference in the two solutions.
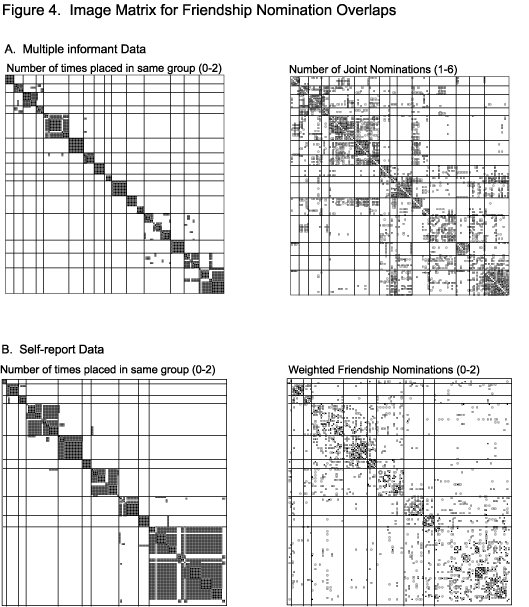
Now consider the self-nomination case in panel B. The lower overall agreement is evident in the larger number of gray cells, but note also the greater diversity of tie distribution in the raw data in the second matrix. The region of greatest disagreement is in the lower-right of the adjacency matrix. Here we see that PCA and RNM agreed on the pairwise assignment of those nodes with the strongest ties, but PCA split the set into many small groups and RNM kept them together. This is exactly the trade-off between distinction and density alluded to above.
This tradeoff becomes more apparent if we zoom in on the region of the self-reported friendship network where the three approaches disagree most: the large ‘tangle’ of reciprocated relations on the male side of Figure 1. Figure 5 plots the 60 nodes involved in this set, identifying groups with four different methods. To ease comparison, the figures use the same layout for each solution, but colors and shaded regions encapsulate nodes according to how each algorithm clustered the data set.[13] The figure includes the three indirect clustering routines compared here, as well as a cohesive blocking routine described by Moody & White (2003), which helps inform why the other three solutions differ. To help visualize the cluster results, nodes of the same color are enveloped in a semi-transparent region shaded the same color as the nodes.
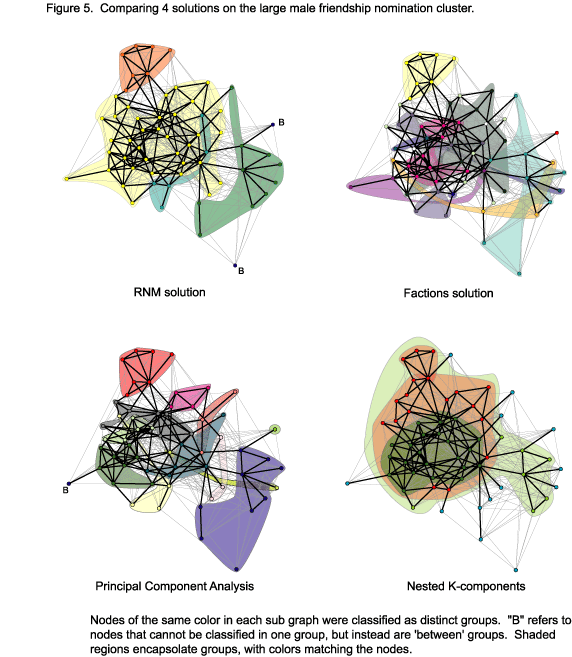
The three clustering methods agree exactly on the grouping of the seven nodes at the top of the figure and have relatively similar assignments of the nodes around the nine-person star at the far right of the figure. These nine nodes center around a central actor, and every solution finds a group centered around this actor, although they differ slightly on their exact composition. The yellow section in the RNM solution, however, dominates the bulk of this subgraph. If you look carefully across the three solutions, you see little agreement on the placement of nodes within this set.[14] The FAC solution crosses the strongest tie section in multiple ways (other layouts, that do not weight reciprocated ties for example, do not help here). The PCA solution provides more compact divisions, but a number of points spread over the bulk of this tangle. The RNM approach just called it a single group.
Why is it so difficult to consistently partition this section? The answer lies in the direct blocking given in the lower-right panel of Figure 5. Instead of identifying primary groups, here we employ a cohesive blocking of the graph. A cohesive block contains nodes that are similarly situated in the node-independent path structure (here based solely on the reciprocated-tie network). If a component is k-connected, then the graph cannot be divided into separate pieces unless at least k nodes are removed (Moody & White 2003). All nodes are part of the 1-component, but nested within this set is a 47-person bicomponent, two 3-components (size 4 – the heart of the section all methods agree on; and size 35 – the large orange region), and the core of this network is a 22-person 4-component (olive green section) that admits to no more strongly linked k-components.[15]
Node connectivity provides a natural boundary for primary groups, as the cutpoints in the graph provide a clear partition of edges into distinct sets. Since there is no natural split in the cohesion structure to exploit, the resulting divisions are based on other graph features.[16] FAC appears to incorporate weak-ties, while the PCA solution appears to use both the weak tie information and capitalize on the increase in correlation that comes from two actors not being connected to similar third parties. This element of structural equivalence is evident in the light pink trio composed of actors all connected to a central star (that is in another group), and perhaps suggests one mechanism to explain the greater homogeneity within group. RNM, in contrast, focuses largely on group distinctiveness, building on these cutponts, and thus does not attempt to split this group.
IV. Conclusion and Discussion
Are investigators who use different data collection methods and different analysis techniques to find adolescent “peer groups” studying the same thing? Our results suggest that (for these data) all methods find roughly similar groups, but that: (a) the differences that do appear are systematically and strongly affected by the data collection method, depending more on the group detection algorithm for self-reported friendship data; (b) when detection algorithms differ, they trade off the extent to which detected groups are distinct from the rest of the network rather than internally dense and (c) algorithms favoring internally dense ties identify groups with greater behavioral similarity.
With respect to data, the multi-informant data produces easier targets for any algorithm to cluster. We suspect that the substantial difference in the “clusteredness” of the self-reported friendship and multi-informant group data follows largely from differences in the level at which affiliations are reported (dyads vs. groups). Lists of dyadic friendships do not imply direct ties among the friends listed. In contrast, recorded responses at the level of groups are completely connected (and distinct) cliques, so the resulting networks have to look like overlaps of cliques. Differences in the clusteredness of the two types of data were further magnified by the fact that adolescents listed nearly twice as many peers in response to the groups question (M = 17.3) as they did when they listed only their own friends (M =9.72). Finally, it is possible that there are differences in the transitivity of (peer-perceived) interaction patterns and (self-reported) affective ties: in other words, feelings of friendship may be more diffusely organized than the interaction patterns perceived by peers. Within these data, we cannot disentangle how each of these factors (group-vs-dyad; multi-vs.-self-informant; interaction-vs.-closeness) contributed to the greater clusteredness of the multi-informant data, but together they clearly resulted in substantial differences in the data structures from which groups were derived.
In comparing detection algorithms, the RNM procedure is biased toward identifying groups that are distinct from each other, while FAC and PCA find groups that are more internally dense, even if they are not strongly distinct from other groups in the network. The tension between group distinctiveness (RNM) and internal density (FAC, PCA) is most apparent when the network structure does not lend itself to a set of clearly discrete groups, such as with the friendship data (Figure 5). The fact that the smaller, denser groups identified by FAC and PCA are more behaviorally homogenous than the larger groupings identified by RNM suggests that they are making non-random differentiations within the large “tangle” of relationships. The tension between grouping algorithms that emphasize distinctiveness over internal density may be reduced by allowing groups to overlap. In the PCA procedure, for example, significant loadings on two factors can be interpreted as instances of membership in two overlapping groups: explicitly permitting such “dual-membership” would likely decrease the number of closed triads that are split when these individuals are forced to be members of only one group.
It is noteworthy that behavior similarity was higher within groups identified by PCA than within groups identified by the other two algorithms. Why would this be true, particularly given RNM’s theoretical foundation in peer influence models? Two explanations deserve further examination. First, PCA uses a profile similarity score (the correlation of ties across all actors), which is a classic measure of structural equivalence. Finding a stronger behavioral effect for PCA groups over the other two algorithms suggests future work might focus on role-based mechanisms that are related to a group’s position in the overall network structure (Burt, 1978, 1987; Friedkin, 1984; Mizruchi, 1993). Second, it might be that dyads, rather than groups, are the relevant unit for influence in early adolescence. Developmental researchers have suggested that group-level dynamics and influence begin during adolescence (Rubin et al., 1998), but systematic research clarifying exactly when these processes emerge is lacking. If dyad-level influences prevail in early adolescence, then the slight advantage in dyadic strength identified within the PCA groups makes it a better proxy of those processes.
The RNM routine implements a behavior model that assumes equal influence of similarly weighted ties, but recent sociological work on social influence (Friedkin, 1998; Friedkin and Johnsen, 1997; Haynie, 2001) suggests that peers are counted differentially based on their position. One way to test this assumption would be to generate RNM similarity scores that interact with peer position, giving higher weights to central actors or the number of third parties commonly joining each pair. Developmental researchers are moving in a similar direction by considering strategies that would differentially weight peers in the social network based on information about both friendship ties and interaction frequency (Kindermann, 1996). For example, extra weight could be assigned to friends within interaction-based groups, or reciprocated friends could be weighted according to the number of peers who report that they “hang around together a lot.”
What general recommendations about data collection and group detection method can be made from this comparison? First, it is clear that the group membership results depend strongly on the data collection method and it appears that the most relevant feature of the method depends on the level of density and transitivity / clustering it generates. Second, while we find a generally broad consensus across methods and data, when these grouping methods disagree, it tends to be along a dimension of distinction vs. density. With the typically sparser and less clustered self-reported friendship data, researchers should recognize this probable disagreement across methods and provide a clear theoretical rationale for why density would be preferable to distinction (or vice versa). Researchers might ideally seek evidence of the generalizability of substantive conclusions by comparing substantive conclusions across multiple grouping algorithms applied to the same network or the same grouping algorithm applied across multiple networks. When there are not compelling conceptual or logistical reasons to measure peer groups in terms of self-reported friendships, then collecting data in the form of multi-informant groups will likely provide a more robust basis for group identification.
Future research should more fully explore several issues that were beyond the scope of these analyses. Most fundamentally, if peer similarity and influence operate mainly at the dyadic level in early adolescence, might it be more efficient to focus on these direct ties and forego the identification of group structures altogether? At what stage in development do group structures add explanatory power over and above direct ties? How might allowing for overlap among groups affect differences among group solutions and estimates of behavioral similarity? How might information about friendships and interaction-based social ties be combined to weight peers differentially according to their likely influence? Given that both developmental and sociological network researchers have articulated similar questions and potential solutions to these questions, continued cross-fertilization of conceptual, methodological and analytic methods should produce benefits for both fields.
References
Asher, S. R., and J. Coie (eds.). (1990). Peer Rejection in Childhood. Cambridge: Cambridge University Press.
Bagwell, C. L., J. D. Coie, R. A. Terry, and J. E. Lochman. (2000). Peer clique participation and social status in preadolescence. Merrill-Palmer Quarterly: Journal of Developmental Psychology 46: 280-305.
Batagelj, V., and A. Mrvar. (2001). PAJEK. Vers. 71.
Bell, R. R. (1988). Worlds of Friendship. Beverly Hills: Sage Publications.
Berndt, T. J. (1982). The features and effects of friendship in early adolescence. Child Development 53 (6): 1447-1460.
———. (1992). Friendship and friends' influence in adolescence. Current Directions in Psychological Science 1: 156-159.
Berndt, T. J., and S. G. Hoyle. (1985). Stability and change in childhood and adolescent friendships. Developmental Psychology 21: 1007-1015.
Berndt, T. J., and L. M. Murphy. (2002). Influences of friends and friendships: Myths, truths, and research recommendations. In Advances in Child Development and Behavior 30: 275-310.
Bock, R. D., and S. Z. Husain. (1952). Factors of the tele: A preliminary report. Sociometry 15: 206-219.
Boivin, M., and S. Hymel. (1997). Peer experiences and social self-perceptions: A sequential model. Developmental Psychology 33 (1): 135-145.
Borgatti, S., M. G. Everett, and L. C. Freeman. (1999). UCINET V for Windows: Software for Social Network Analysis. Vers. 5.2.0.1. Natick, MA: Analytic Technologies.
Bukowski, W. M., A. F. Newcomb, and W. W. Hartup (eds.) (1996). The Company They Keep: Friendships in Childhood and Adolescence. New York: Cambridge University Press.
Burt, R. S. (1978). Cohesion versus structural equivalence as a basis for network sub-groups. Sociological Methods and Research 7: 189-212.
———. 1987. Social contagion and innovation: Cohesion versus structural equivalence. American Journal of Sociology 92: 1287-335.
Cairns, R. B. (1979). Social Development: The Origins and Plasticity of Social Interchanges. San Francisco: Freeman.
Cairns, R. B., and B. D. Cairns. (1994). Lifelines and Risks: Pathways of Youth in Our Time, New York: Cambridge University Press.
Cairns, R. B., B. D. Cairns, H. J. Neckerman, S. D. Gest, and J. L. Gariepy. (1988). Social networks and aggressive-behavior: Peer support or peer rejection? Developmental Psychology 24: 815-823.
Cairns, R. B., M. C. Leung, L. Buchanan, and B. D. Cairns. (1995). Friendships and social networks in childhood and adolescence: Fluidity, reliability, and interrelations. Child Development 66: 1330-1345.
Cairns, R. B., J. E. Perrin, and B. D. Cairns. (1985). Social structure and social cognition in early adolescence: Affiliative patterns. Journal of Early Adolescence 5: 339-355.
Cohen, J. M. (1977). Sources of peer group homogeneity. Sociology of Education 50: 227-241.
Coie, J. D., K. A. Dodge, and H. Coppotelli. (1982). Dimensions and types of social status: A cross-age perspective. Developmental Psychology 18 (4): 557-570.
Coleman, J. S. (1961). The Adolescent Society: The Social Life of the Teenager and its Impact on Education. New York: Free Press.
Dishion, T. J., S. E. Nelson, C. E. Winter, and B. M. Bullock. (2004). Adolescent friendship as a dynamic system: Entropy and deviance in the etiology and course of male antisocial behavior. Journal of Abnormal Child Psychology 32 (6): 651-663.
Doreian, P., R. Kapuscinski, D. Krackhardt, and J. Szczypula. (1996). A brief history of balance through time. Journal of Mathematical Sociology 21 (1-2): 113-31.
Estell, D. B., R. B. Cairns, T. W. Farmer, and B. D. Cairns. (2002). Aggression in inner-city early elementary classrooms: Individual and peer-group configurations. Merrill Palmer Quarterly 48: 52-76.
Farmer, T. W., D. B. Estell, J. L. Bishop, K. K. O’Neal, and B. D. Cairns. (2003). Rejected bullies or popular leaders? The social relations of aggressive subtypes of rural African American early adolescents. Developmental Psychology 39 (6): 992-1004.
Feld, S. L. (1981). The focused organization of social ties. American Journal of Sociology 86: 1015-35.
Fershtman, M. (1997). Cohesive group detection in a social network by the Segregation Matrix Index. Social Networks 19: 193-207.
Frank, K. A. (1995). Identifying cohesive subgroups. Social Networks 17: 27-56.
Freeman, L. C. (1972). Segregation in social networks. Sociological Methods and Research 6: 411-30.
———. (1992). The sociological concept of "group": An empirical test of two models. American Journal of Sociology 98: 152-66.
———. (2003). Finding groups: A meta-analysis of the Southern Women Data. In Dynamic Social Network Modeling and Analysis, edited by R. Breiger, K. Carley, & P. Pattison. Washington: The National Academies Press.
Friedkin, N. E. (1984). Structural cohesion and equivalence explanations of social homogeneity. Sociological Methods and Research 12: 235-61.
———. (1998). A Structural Theory of Social Influence. Cambridge: Cambridge University Press.
Friedkin, N. E., and K. S. Cook. (1990). Peer group influence. Sociological Methods and Research 19 (1): 122-43.
Friedkin, N. E., and E. C. Johnsen. (1997). Social positions in influence networks. Social Networks 19: 209-22.
Gest, S. D., T. W. Farmer, B. D. Cairns, and H. Xie. (2003). Identifying children’s peer social networks in school classrooms: Links between peer reports and observed interactions. Social Development 12: 513-529.
Gest, S. D., K. L. Rulison, and J. A. Welsh. (2005, May). Friendship, Interaction Frequency and Shared Group Membership as Determinants of Peer Similarity and Influence. Poster presented at the Society for Prevention Research, Washington, DC, May 26.
Giordano, P. C., S. A. Cernkovich, H. T. Groat, M. D. Pugh, and S. Swinford. (1998). The quality of adolescent friendships: Long term effects? Journal of Health and Social Behavior 39: 55-71.
Guimera, R., and L. A. N. Amaral. (2005). Functional cartography of complex metabolic networks. Nature 433: 895-900.
Hallinan, M. T. (1978). The process of friendship formation. Social Networks 1: 193-210.
Hallinan, M. T., and N. B. Tuma. (1978). Classroom effects on change in children's friendship. Sociology of Education 51: 270-282.
Hanish, L. D., C. L. Martin, R. A. Fabes, S. Leonard, and M. Herzog. (2005). Exposure to externalizing peers in early childhood: Homophily and peer contagion processes. Journal of Abnormal Child Psychology 33 (3): 267-281.
Hartup, W. W. (1996). The company they keep: Friendships and their developmental significance. Child Development 67: 1-13.
Haynie, D. (2001). Delinquent peers revisited: Does network structure matter? American Journal of Sociology 106: 1013-57.
Hektner, J. M., G. J. August, and G. M. Realmuto. (2000). Patterns and temporal changes in peer affiliation among aggressive and nonaggressive children participating in a summer school program. Journal of Clinical Child Psychology 29 (4): 603-614.
Holland, P., and S. Leinhardt. (1977). A dynamic model for social networks. Journal of Mathematical Sociology 5: 5-20.
Holland, P. W., and S. Leinhardt. (1970). A method for detecting structure in sociometric data. American Journal of Sociology 70: 492-513.
———. (1971). Transitivity in structural models of small groups. Comparative Groups Studies 2: 107-24.
Homans, George C. (1992 [1950]). The Human Group. New Brunswick, NJ: Transaction [Harcourt, Brace & World].
Jussim, L., and D. Osgood. (1989). Influence and similarity among friends: An integrative model applied to incarcerated adolescents. Social Psychology Quarterly 52 (2): 98-112.
Kindermann, T. A. (1993). Natural peer groups as contexts for individual development: The case of children's motivation in school. Developmental Psychology 29: 970-966.
———. (1996). Strategies for the study of individual development within naturally-existing peer groups. Social Development 5: 159-173.
Krackhardt, D. (1987). Cognitive social structures. Social Networks 9: 109-34.
Ladd, G. W. (1983). Social networks of popular, average, and rejected children in school settings. Merrill-Palmer Quarterly: Journal of Developmental Psychology 29: 283-307.
MacRae, J. (1960). Direct factor analysis of sociometric data. Sociometry 23: 360-371.
Mizruchi, M. S. (1993). Cohesion, equivalence and eimilarity of behavior: A theoretical and empirical assessment. Social Networks 15: 275-307.
Moody, J. (2001a). Peer influence groups: Identifying dense clusters in large networks. Social Networks 23: 261-283.
———. (2001b). Race, school integration, and friendship segregation in America. American Journal of Sociology 107: 679-716.
Moody, J., and D. R. White. (2003). Social cohesion and embeddedness: A hierarchical conception of social groups. American Sociological Review 68: 103-127.
Morey, L. C., and A. Agresti. (1984). The measurement of classification agreement: An adjustment to the Rand Statistic for Chance Agreement. Educational and Psychological Measurement 44: 33-37.
Mrug, S., B. Hoza, and W. M. Bukowski. (2004). Choosing or being chosen by aggressive-disruptive peers: Do they contribute to children's externalizing and internalizing problems? Journal of Abnormal Child Psychology32 (1): 53-65.
Newcomb, A. F., and C. L. Bagwell. (1995). Children's friendship relations: A meta-analytic review. Psychological Bulletin 117 (2): 306-347.
Newman, M. E., and M. Girvan. (2004). Finding and evaluating community structure in networks. Physical Review E. 69: no. 026113.
Patterson, G. R. (1974). A basis for identifying stimuli which control behavior in natural settings. Child Development 45: 900-911.
Patterson, G. R. (1982). A Social Learning Approach (Vol. 3): Coercive Family Process. Eugene, OR: Castalia Publishing.
Rand, W. M. (1971). Objective criteria for the evaluation of clustering methods. Journal of the American Statistical Association 66: 846-50.
Richards, W. D. (1995). NEGOPY. Vers. 4.30. Burnaby, B.C. Canada: Simon Fraser University.
Rodkin, P. C., T. W. Farmer, R. Pearl, and R. Van Acker. (2000). Heterogeneity of popular boys: Antisocial and prosocial configurations. Developmental Psychology 36 (1): 14-24.
Rubin, K. H., W. Bukowski, and J. G. Parker. (1998). Peer interactions, relationships, and groups. In N. Eisenberg (ed.), Handbook of Child Psychology: Social, Emotional and Personality Development (5th ed., pp. 619-700). New York: Wiley.
Sampson, S. F. (1969), A Novitiate in a Period of Change: An Experimental and Case Study of Social Relationships. Unpublished doctoral dissertation. Ithaca, NY: Cornell University.
Seidman, S., and B. Foster. (1978). A graph-theoretic generalization of the clique concept. Journal of Mathematical Sociology 6: 139-54.
Simmel, G. (1950). The Sociology of Georg Simmel, K.H. Wolf (ed.). New York: The Free Press.
Snyder, J., E. Horsch, and J. Childs. (1997). Peer relationships of young children: Affiliative choices and the shaping of aggressive behavior. Journal of Clinical Child Psychology 26 (2), 145-156.
Strayer, F., and A. J. Santos. (1996). Affiliative structures in preschool peer groups. Social Development 5: 117-130.
Sullivan, H. S. (1953). The Interpersonal Theory of Psychiatry. New York: W.W. Norton.
Urberg, K. A., S. M. Degirmencioglu, J. M. Tolson, and K. Halliday Scher. (1995). The structure of adolescent peer networks. Developmental Psychology 31: 540-547.
Vaughn, B. E., and E. Waters. (1981). Attention structure, sociometric status, and dominance: Interrelations, behavioral correlates, and relationships to social competence. Developmental Psychology 17: 275-288.
Watts, D. J. (1999). Networks, dynamics, and the Small-World phenomenon. American Journal of Sociology 105: 493-527.
White, H. C., S. A. Boorman, and R. L. Breiger. (1976). Social structure from multiple networks I: Blockmodels of roles and positions. American Journal of Sociology 81: 730-780.
Wright, B. D. and M. S. Evitts. (1961). Direct factor analysis in sociometry. Sociometry 24: 82-98.
Xie, H., R. B. Cairns, and B. D. Cairns. (1999). Social networks and configurations in inner-city schools: Aggression, popularity, and implications for students with EBD. Journal of Emotional and Behavioral Disorders 7 (3): 147-155.