Network Role Analysis in the Study of Food Webs:
An Application of Regular Role Coloration[1]
Jeffrey C. Johnson
Department of Sociology
East Carolina University
Stephen P. Borgatti
Carroll School of Management
Boston College
Joseph J. Luczkovich
Department of Biology
East Carolina University
Martin G. Everett
Department of Mathematics
University of Greenwich
ABSTRACT: In the last fifteen years, ecosystem ecologists have
developed a theoretical approach and a set of computational methods
called
“ecological network analysis” (Ulanowicz, 1986; Kay et al. 1996).
Ecological network analysis is based on input/output models of energy
or material flows (e.g., carbon compound flows) through a trophic
network (e.g., a food web describing which species eats which other
species). Mathematically and conceptually, this ecological network
analysis approach is strikingly similar to work in the field of social
network analysis, particularly the influence models of Hubbell (1965),
Katz (1963), and Friedkin and Johnsen (1990). In food web research,
Yodzis and Winemiller (1999), have recently proposed a new way to
operationalize the concept of a "trophospecies", which is a set of
species with similar foods or predators. Their definition turns out
to be identical to the notion of structural equivalence (Lorrain and
White,
1971) in social network analysis, particularly as conceived by Burt
(1976) and
Burt and Talmud (1993). The striking convergence to date of the fields
of ecology and sociology via independent invention of network concepts
suggests that there may be considerable value in cross-fertilization of
the two fields. With this paper we hope to begin a dialogue between the
two fields, by applying advanced social role theory and methods to the
study of food webs. In social network analysis, the introduction of the
notion of structural equivalence thirty years ago was followed by the
development of regular coloration (White & Reitz, 1983; Everett
& Borgatti, 1991), an important advance over structural equivalence
for modeling social roles. The objective of our paper is to answer a
call in the ecological literature for greater clarity in thinking about
the role of species in ecosystems (Simberloff and Dayan, 1991), by
applying the notion of regular
coloration to food webs.
Introduction
Ecologists have long been interested in interactions among species, particularly in the sub-fields of community and ecosystem ecology. In the last fifteen years, ecosystem ecologists have developed a theoretical approach and a set of computational methods called “ecological network analysis” (Ulanowicz, 1986; Kay et al. 1996). Ecological network analysis is based on input/output models of energy or material flows (e.g., carbon compound flows) through a trophic network (e.g., a food web describing which species eats which other species). In addition, several other network approaches to studying food webs are beginning to be developed in ecology, especially in terrestrial ecosystems (see Polis and Winemiller 1995 for a review of the various approaches).
Research efforts using network analyses in ecology have produced methodological, theoretical and empirical advances. Two main software packages have been developed to perform ecological network analysis: NETWRK4 (Ulanowicz 1987; software downloads available at http://www.cbl.cees.edu/~ulan/ntwk/network.html) and ECOPATH (Christensen and Pauly 1992). These network analysis programs have been used to model trophic relationships among primary producers, herbivores, intermediate consumers, top predators, and dead material (detritus and carrion) in food webs, providing opportunities for comparative analysis of whole ecosystems measured at different places and times. The food web is modeled as a series of n compartments into which energy or materials flow and leave, with input from and export to other ecosystems, and respiration to the atmosphere for each compartment incorporated into the network. Each species in a food web can be assigned its own compartment, or more typically, species are grouped into compartments based on similarity of diet. An n x n matrix of compartments with material or energy flows moving from producers to consumer compartments is then set up. This matrix can be analyzed for total system throughput, average path length, the presence of cycles, the sources or sinks of material, and the trophic level of any given compartment.
Comparative ecosystem analysis using ecological network models derived from empirical data has been used to study whole ecosystem productivity, growth and development of ecosystems, and to provide a measure of ecosystem stress. For example, Baird and Ulanowicz (1989) used the network analysis approach to compare the seasonal changes in the Chesapeake Bay, clarifying the importance of the planktonic and benthic subsystems in the network to overall productivity at different times of the year. Baird and Ulanowicz (1993) compared four estuary ecosystems in Europe and South Africa, including one polluted ecosystem, using network analysis to analyze the trophic structure of each ecosystem and assess the relative amount of stress or ecosystem maturity. Monaco and Ulanowicz (1997) employed ecological network analysis to compare trophic structure and total system productivity of three estuaries in the mid-Atlantic region of the USA: Narragansett Bay, Delaware Bay and Chesapeake Bay, listed here in decreasing order of overall production and increasing order of stress. Baird et al. (1998) described the trophic relationships and cycles of carbon fluxes in a seagrass meadow using network analysis, comparing variations in the carbon flow dynamics across four sampling sites within a single estuary. Christian and Luczkovich (1999) used ecological network analysis to produce a ranking of each species in a food web by their effective trophic levels (Levine 1980), which is a fractional measure of the number of trophic links carbon compounds had passed through after being fixed by primary producers in a seagrass ecosystem. A compilation of many such network analysis models and their application to aquatic ecosystems, including studies of fisheries and aquaculture systems, was recently produced (Christensen and Pauly 1993). Thus, ecological network analysis has been widely adopted in aquatic ecosystem analysis as an empirical tool for following carbon and other nutrient flows, describing carbon sources and sinks, mapping trophic levels and energy flow among these levels, and examining the dependency of various species on particular sources of energy as it changes over space and time.
Network analysis has been used to develop ecosystem theory, notably in the area of ecosystem maturity. The theory of ecosystem “ascendancy” has been articulated by Ulanowicz (1997), which states that as an ecosystem network develops through time in a stable environment, it becomes more hierarchical and has fewer redundant links. A state of high ecosystem ascendancy -- a network-based measure that has been proposed by Ulanowicz (1986) -- has been used to describe this trend. In an unstable environment or in an early stage of network development, there are many redundant links, a lack of hierarchical structure, and thus low ecosystem ascendancy. The network measure of ecosystem stress is based on the frequency of redundant connections; whereas a mature or non-stressed network have few redundant connections, a polluted, stressed, or frequently disturbed network will have many redundant connections. Thus, a new ecological theory has been proposed based on network studies that suggest mature ecosystem networks have higher ascendancy than immature ecosystems -- a measure that has been derived from network analyses.
Mathematically and conceptually, ecological network analysis is strikingly similar to work in the field of social network analysis, particularly the influence models of Hubbell (1965), Katz (1963), and Friedkin and Johnsen (1990). In food web research, ecologists Yodzis and Winemiller (1999) have recently proposed a new definition and operationalization of the concept of a "trophospecies," which is a collection of species in a food web that have similar foods and predators. Their definition turns out to be identical to the notion of structural equivalence (Lorrain and White, 1971) in social network analysis, particularly as conceived by Burt (1976) and Burt and Talmud (1993).
The striking convergence to date of the fields of ecology and sociology via independent invention of network concepts suggests that there may be considerable value in cross-fertilization of the two fields. In particular, sociology in general and social network analysis in particular has focused heavily on structural analysis (Mayhew, 1980), dedicating whole conferences and journals (such as the Journal of Social Structure) to the topic. As a result, it has developed a rich set of structural concepts and computational procedures. Structural concepts are equally important in ecology, but have received somewhat less methodological attention, particularly concerning some of the role approaches discussed in this article. Consequently, ecology may be in a position to benefit from the extraordinary development of structural methodologies in the social sciences whereas the social sciences may be in a position to benefit from some of the network theoretical advancements in ecology.
With this paper we hope to begin a dialogue between the two fields, by applying advanced social role theory and methods to the study of food webs. In social network analysis, the introduction of the notion of structural equivalence thirty years ago was followed by the development of regular coloration (White & Reitz, 1983; Everett & Borgatti, 1991), an important advance over structural equivalence for modeling social roles. The objective of our paper is to answer a call in the ecological literature for greater clarity in thinking about the role of species in ecosystems (Simberloff and Dayan, 1991), by applying the notion of regular coloration to food webs.
In Search of a Formal Definition of Role
In recent years, the social sciences have paid much attention to the importance of structure in understanding human behavior at both the macro and micro levels of analysis (Mayhew, 1980). One area of particular interest has been the study of social roles. Social scientists have devoted a considerable amount of effort to understand the relationship between the position of an actor in set of structured relations and the role (or roles) of that actor within the system. Such work has been influenced by a general concern in the social sciences for producing theoretical definitions of a social role. Earlier social theorists such as Homans (1967), Goodenough (1969), Nadel (1957), and Merton (1957) produced conceptual definitions of social roles that went beyond simple inventories of rights and obligations, and instead defined roles relationally in terms of their characteristic pattern of ties with other roles. For these theorists, what defines a person as playing the role of doctor is the characteristic set of relations they maintain with persons who are playing related roles such as patients, nurses, medical record keepers, pharmaceutical sales people, receptionists, etc. The relations associated with these roles are structured and patterned in predictable ways and may vary only slightly from one medical practice to another.
This relational conception of the notion of social role lends itself well to formal modeling. Early network researchers such as White (1963) and Boyd (1969) initiated what might be termed formal network role analysis in their attempts to model kinship systems using algebraic approaches. This was followed by Lorraine and White’s (1971) seminal work on structural equivalence that sought to not only formally define roles in terms of the structure of human relations, but to reduce the complexity of a network of relations in terms of sets of simplified role structures (i.e., images). This work has been followed by the formulation of a variety of equivalence approaches that define in various ways the relational properties that sets of actors must have in order for them to be equivalent in terms of the roles and positions they occupy (Wasserman and Faust 1995). We will return to this in more detail in a later section of the paper.
The Idea of a Species Role in Ecology
An important issue for ecologists has been to conceptualize the roles of species in an ecological community. The niche concept, for example, was defined early on by Elton (1927) as the "fundamental role" of an organism in a community; its relationship to predators and prey. In fact, Elton's original discussion of an organism's role was based explicitly on social roles in human communities (ibid. 63-64):
“It is therefore convenient to have some term to describe the status of an animal in its community, to indicate what it is doing and not merely what it looks like, and the term used is "niche." Animals have all manner of external factors acting upon them -- chemical, physical, and biotic -- and the "niche" of an animal means its place in the biotic environment, its relations to food and enemies. The ecologist should cultivate the habit of looking at animals from this point of view as well as from the ordinary standpoints of appearance, names, affinities, and past history. When an ecologist says "there goes a badger" he should include in his thoughts some definite idea of the animal's place in the community to which it belongs, just as if he had said "there goes the vicar."” (Emphasis is Elton's.)
Role-like concepts have become a central concern for researchers interested in trophic (i.e., eating-based) views of ecosystems (Yodzis and Winemiller, 1999). Dissatisfied with early approaches to the trophic level concept, which are now seen as too coarse, broad, or even arbitrary to be useful, some ecologists have sought to develop new trophic concepts that better capture the inherent complexity of systems of trophic interactions (Cousins 1987; Polis 1991). These newer approaches often refer to the functional role (Cummins, 1974) of a species (or sets of related species) in a community, and also tend to see these roles as “basic building blocks” (Hawkins and MacMahon, 1989) of communities and therefore aids in reducing the complexity of an ecological system.
One of the most widely used trophic role concepts is the guild. Guilds are subdivisions of units of analysis that share similar prey. They are groups of species exploiting a common resource base in a similar fashion (Root, 1967). What is important to note here is that two species are members of the same guild to the extent that they have exactly the same prey. Although this captures an aspect of the role of a species or class of species in a food web, it only considers a species role with regard to downward trophic interactions; predators are not considered. Yodzis (1988:508) discussed a related concept called trophospecies, which he defined as “a lumping together of biospecies with similar [emphasis ours] feeding habits.” As we shall see, this downward orientation of the trophospecies concept was later extended to include trophic interactions in both directions.
Several ecologists have attempted to expand the idea of a species trophic role to include simultaneously interactions involving predators as well as prey. For example, Pimm et al. (1991) advanced the trophospecies concept as the aggregation of species that have identical predators and prey. Goldwasser and Roughgarden (1993) have suggested the concept of trophically equivalent species or species that share the same sets of predators and prey. An important part of the logic of Goldwasser and Roughgarden is the intuitive notion that similarities in diets may or may not imply similarities in predators. Similarly, Persson et al. (1996) sought to expand the trophic role concept to include both upward and downward interactions. One of the concepts they suggested was that of the trophic group in which species, or clusters of species, have similar dynamics because they share the same predators and the same prey. Although all of these role concepts can be considered conceptual advancements, the authors provide little in the way of how these concepts can be formally operationalized. Further, clarification of these concepts is hampered by the confusion surrounding what is meant by the terms similar and same. As Yodzis (1988:508) notes in a discussion of some of the problems with methods for species aggregations in food webs[2] “of course a shortcoming of existing food web data is the lack of a consistent usage for 'similar' in this context; for the foreseeable future we are just going to have to live with this.”
In response to these basic problems, Yodzis and Winemiller (1999) have recently provided a formalization of the notion of trophospecies -- species aggregated on the basis of having similar roles in a food web -- that takes into account linkages to both predators and prey and more clearly delineates what is meant by similar. They recommend using the Jaccard (1900) similarity index for binary data (as well as an analogous index for continuous data) in which the similarity between species i and j is
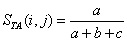
Where a refers to the total of both predator and prey that species i and j share, b represents the number of species of
both predators and prey that i has but not j, and c gives the number of species of both predators and prey that j has but not i.
They then employ cluster analysis of the matrix of Jaccard coefficients
in order to produce aggregations of species based on trophic
similarity.
Role Coloration and Trophic Roles
To any social network researcher, it is obvious that Yodzis and Winemiller’s approach to trophospecies in a food web is essentially the same as the notion of structural equivalence in a social network introduced in the sociological literature thirty years ago by Lorrain and White (1971), and is virtually identical to the version popularized by Burt (1976).[3] In fact, the Jaccard coefficient proposed by Yodzis and Winemiller is an option in the structural equivalence procedure found in the UCINET 5 social network analysis software package (Borgatti, Everett and Freeman, 1999).
However, in the social networks literature, the introduction of structural equivalence eventually gave rise to a more general notion -- regular coloration -- that better captured the theoretical notion of social role (White and Reitz, 1983; Everett and Borgatti, 1991). Although structural equivalence captures perfectly the notion of competition, it has limitations when used to define social role. In structural equivalence, two actors are equivalent if they have the same relations with the same others. That means that two mothers, each with three children, and each with two parents, are not seen as playing the same role (i.e., are not structurally equivalent), since (presumably) they are not mothers to the same children and not born of the same parents. Similarly, if we divide up a network of people into structurally equivalent classes, then if a person Bill in one structural class has a certain kind of tie to a person Mary in another class, then everyone in Bill’s class must have that same kind of tie with Mary, and Bill must have that tie with everyone in Mary’s class. But this strange restriction is not part of the theoretical concept of role, since we recognize that two corporate Presidents play the same role, even though the boards they report to are different and they have different subordinates. Consequently, a new approach was needed to model the notion of social role, and this approach was regular coloration.
In the regular coloration model, we assign colors to nodes such that if two persons are assigned the same color (i.e., are playing the same role), then they are connected to equivalent (but not necessarily the same) others. To define the concept more formally, we introduce some notation. Let G(V,E) denote a directed graph with set of nodes V and set of ties E. We write (u,v)ÎE if there is a tie from u to v. Let the out-neighborhood of a node v be denoted No(v) and defined as the set of nodes that have a tie from v to them. That is, No(v) = {x | (v,x) Î E}. Similarly, the in-neighborhood of v is denoted Ni(v) and defined as Ni(v) = {x | (x,v) Î E}. The notions of in- and out-neighborhoods are paralleled in ecology by the concepts of “input environs” and “output environs” proposed by Patten (1978). A coloration C is defined as an assignment of colors (classes) to nodes. The color of a node v is denoted by C(v). A coloration is termed regular if it satisfies the following condition:
C(u) = C(v)
-> C(No(u)) = C(No(v))
and C(Ni(u)) = C(Ni(v))
It should be noted that regular coloration actually defines a family of colorations[4], of which structural equivalence (also known as structural coloration) is a member. In this paper, we focus on the most inclusive member of this family, technically known as the maximal regular coloration although, for simplicity of exposition, we shall usually omit the "maximal."
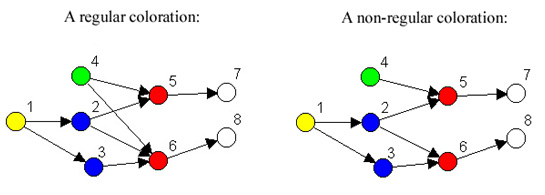
Figure 1. Regular and non-regular role colorations.
Regular coloration can be seen as providing a principled
homomorphic reduction or simplified model of the system of dyadic ties
in a network. For example, the regular coloration in Figure 1 indicates
that although there are eight nodes, there are only five kinds of
nodes, and the way they are related is given in Figure 2.
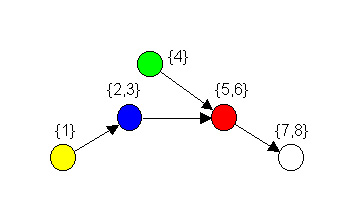
Figure 2. Image graph for regular coloration in Figure 1.
In other words, what is characteristic of red nodes is that they
receive ties from green and blue nodes, and give ties to white nodes.
Looking at Figure 1, it can be seen that in fact every red node
receives a tie from at least one blue node and one green node, and
gives a tie to at least one white node. Similarly what characterizes
blue nodes is that they receive from yellow nodes (and no others) and
give to red nodes (and no others). We refer to the reduced model shown
in Figure 2 as an image graph.
In a food web, the image graph of a regular coloration simplifies
system complexity by providing a reduced model of a food web that loses
very little information, and only in a
strictly defined way. These aggregations of “trophically analogous” or,
what we term isotrophic
species are useful because they reduce complexity
without combining species that are playing different relational roles.
Thus, regular coloration captures some of the functional ideas
discussed by ecologists as it relates to the general trophic roles of
various species.
The regular coloration model may be seen as providing an alternative to the aggregation model proposed by Hirata and Ulanowicz (1985). In their model, the information in a network is defined as the average amount of uncertainty resolved by the knowledge of the network structure. They then use a stepwise heuristic algorithm -- much like a hierarchical clustering algorithm -- to agglomerate species into an arbitrary number of desired classes. The result is a partition that minimizes information loss. In practice, it is possible that in some cases this model will yield answers that resemble regular colorations. However, the answers can also be very different. A key difference between the Hirata-Ulanowicz model and the regular coloration model is that the Hirata-Ulanowicz model is not constrained to collapse only those species that have ties to equivalent others. It is this recursive feature that makes regular coloration distinctive and which makes it so suitable for capturing the notion of role, which carries with it the idea that occupants of the same role have characteristic relations with the occupants of certain other roles.
Regular coloration is also related to the ecological notion of trophic level or trophic position. Trophic level normally refers to the number of links that a species is from the bottom (primary producers) of a food web. It can be proved that in a maximal regular coloration of digraphs without cycles or self-loops, nodes colored the same are equally positioned along corresponding paths passing through them from sources to sinks.[5] In such graphs, then, regularly equivalent nodes will be similarly positioned with respect to distances to (corresponding) producers and also from (corresponding) top predators. For example, in Figure 3, nodes d, e, and g are all regularly equivalent, and they are the same distances from the top (a) and from the bottom (nodes i, j, k) nodes. Similarly, f and h are colored the same, and are the same distances from the top and bottom of the web.
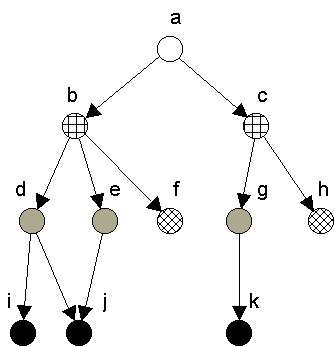
Figure 3. Regular coloration showing source to sink chains.
The relationship between regular coloration and trophic level, while
complex mathematically, is easy to understand at a theoretical level.
Fundamentally, regular coloration is about structural (and presumably)
functional redundancy. As noted by Hirata and Ulanowicz (1985),
functional redundancy is implicit in the notion of trophic level. In
digraphs without cycles or loops, regularly equivalent nodes occupy
identical positions in parallel pathways from sources to sinks; what a
regular homomorphic reduction accomplishes is the elimination of these
parallel pathways to yield a simple model of the original network. [6]
Application of Regular Coloration to Food Web Examples
In this section we examine the application of the regular coloration model to food webs found in the ecological literature. To be useful, the model needs to be able to handle certain features of empirical food webs. For example, the relations among the nodes (called “compartments” by ecologists) of a food web can be either binary (either a species eats something or it doesn’t) or real valued (as in the amount of carbon (mgC/m2) exchanged between compartments). In addition, cannibalism (self-loops) exists, as do cycles (species A eats species B which eats Species A). Fortunately, none of these features is a problem for the regular coloration model.
Another issue pertaining to real-life food webs is the fact that the theoretical models are unlikely to fit perfectly. That is, no species will be perfectly equivalent to another, if only because of measurement error. Consequently, the algorithms used to detect regular coloration must be capable of finding classes of “nearly equivalent” species. There are several approaches available. The one we use in this paper is the profile similarity method embodied in the well-known REGE algorithm (White and Reitz, 1985; Borgatti, Everett and Freeman, 1999). In this approach, we calculate for each pair of nodes the degree of regular equivalence. Details of how this is done are beyond the scope of this paper, but are discussed in Borgatti and Everett (1993). The matrix of regular similarity coefficients is then multidimensionally scaled to provide a visual, spatial representation of the web structure, and cluster-analyzed to produce classes of nearly equivalent nodes. An alternative approach is to use a combinatorial optimization procedure to directly classify nodes into groups so as to minimize a penalty measure based on the regular coloration concept (Batagalj, Doreian and Ferligoj, 1992). The advantage of this approach is that it provides a readily interpretable measure of how well the data actually fit the model. The disadvantage of this approach, and the reason we have not used it here, is that it provides no information (i.e., pairwise similarities or distances) for a spatial representation.
The food webs and isotrophic classes were visualized using MAGE, a three dimensional interactive program originally developed for use in protein chemistry (Richardson and Richardson, 1992, http://kinemage.biochem.duke.edu/). For each of the MAGE graphs, referred to as kinemages, three-dimensional coordinates were obtained through a multidimensional scaling of the regular coefficients similarity matrix. Also, in one of the examples, the Pajek network analysis program (Batagelj and Mrvar, n.d., http://vlado.fmf.uni-lj.si/pub/networks/pajek/) is used to help illustrate the importance of the direction of trophic linkages.
The Mukkaw Bay Intertidal Subweb
Our first simple example is taken from a classic paper on food web complexity and species diversity by Robert Paine (1966). His work was instrumental in illustrating the relationship between the presence of predators and species diversity in an ecosystem. Claiming that subwebs or "groups of organisms capped by terminal carnivores and trophically interrelated in such a way that at higher levels there is little transfer of energy to co-occurring subwebs," are the basic units within biological communities he conducted experiments in the Mukkaw Bay intertidal zone of Washington state (ibid: 66).
Figure 4 provides a representation of Paine's Figure 1 of the feeding relationships of the Pisaster-dominated subweb at Mukkaw Bay (Paine 1966:67).
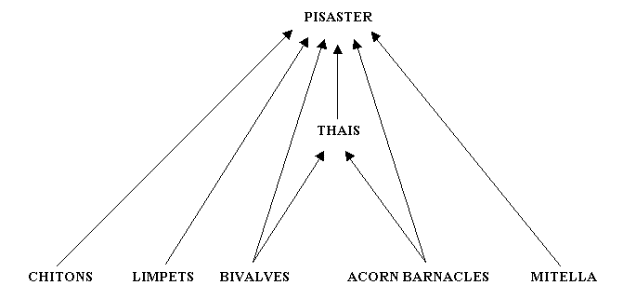
Figure 4. Paine's (1966) conceptualization of the feeding relationships of a subweb in Mukkaw Bay.
Note that this subweb has three levels: herbivorous invertebrates
(chitons [2 species], limpets [2 species], bivalves [1 species],
acorn barnacles [3 species], and goose-necked barnacles [Mitella polymerus]) at the basal level, and two levels of carnivorous predators (Thais emarginata, a snail, as an intermediate predator, and Pisaster
ochraceus,
a sea star, as top predator). It is important to recognize that Paine
did not include primary producers in his depiction of the subweb.
A matrix of trophic relations for this subweb was created and subjected to REGE and graphed using Mage as described above. Figure 5 is an interactive kinemage of the subweb and is strikingly similar to Paine's intuitive graph, with one major exception.
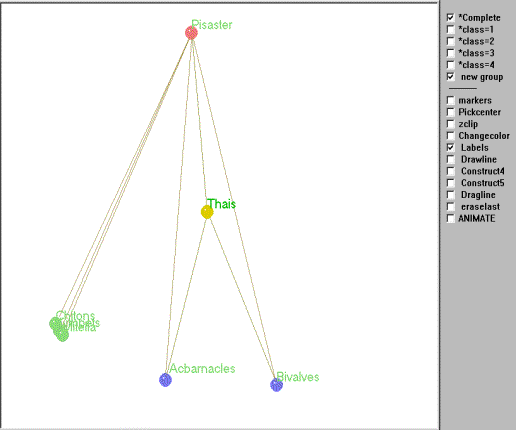
Figure 5. Kinemage of the regular role coloration of the Mukkaw Bay subweb.
To animate Mage, click in the figure (may take a few seconds to load).
Using an average linkage clustering of the regular equivalence
coefficients (see Figure 6) the basal species are aggregated into two
isotrophic classes based on their trophic roles in the subweb
(excluding primary producers). Thus, based on the structure of these
trophic relations there are 4
trophic roles clearly evident. The first of these includes barnacles
and
bivalves that are preyed upon by both Thais and Pisaster, while the second group (chitons, limpets and goose-necked barnacles) are preyed on exclusively by Pisaster. The remaining two groups include both the intermediate (Thais) and top predators (Pisaster).
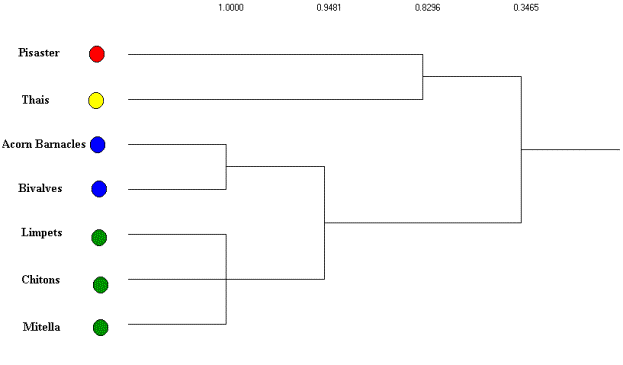
Figure 6. Average linkage clustering of REGE coefficients for
Mukkaw Bay subweb with isotrophic classes identified.
The El Verde Rain Forest
The second example comes from Reagan and Waide (1996) in their examination of the El Verde rain forest food web in Puerto Rico. The matrix contains 156 compartments each containing various levels of species aggregations. For example, some compartments (nodes) contain a single species while others may contain as many as 429 different species. Compartment ties were determined through direct observations while others were inferred from the literature. Species aggregation and lack of direct observation may be problematic in terms the validity of comparisons across systems as well as causing problems with developing and testing theories concerning food web structure. There is an on going debate in ecology concerning these issues, but this is beyond the scope of this paper [see Yodzis and Winemiller (1999) and Polis (1995) for a more detailed discussion].
Based on a hierarchical clustering of REGE coefficients, we have chosen to partition the 156 compartments into six isotrophic classes. Of course, the identification of isotrophic groupings can be at various levels of similarity based on the cluster analysis. In this case, we have chosen few classes in order to explore the structure of the graph at a very general level. The 6-class image graph is shown in Figure 7. This image graph helps in showing both the direction of the trophic relations and which isotrophic classes contain cycles and loops.
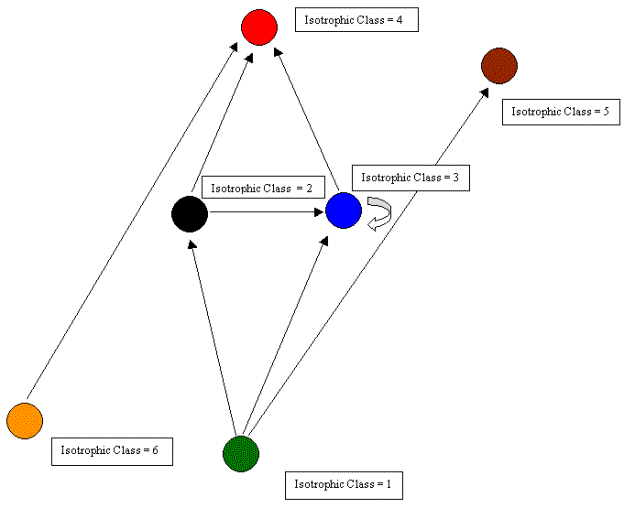
Figure 7. An image graph of the El Verde rain forest food web.
We now turn to a visual representation of the 156-node food web as a whole. The kinemage in Figure 8 shows four main isotrophic groups and two isolated classes (class anomalies).
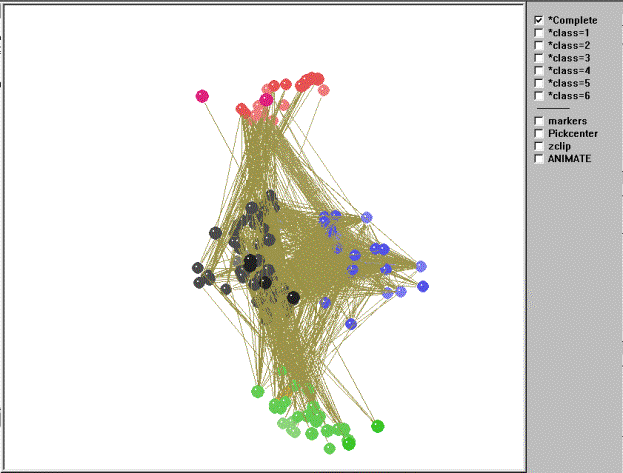
Figure 8. Kinemage of the regular role coloration of the El Verde rain forest.
To animate Mage, click in the figure (may take a few seconds to load).
Top predators (class 4, red), those consumed by no other compartments,
are at one end of the graph. Basal (consumers of producers) and
intermediate consumers (consumers of basal and producers -- classes 3
[blue] and 2 [black, when a white background is selected, as shown
here; this class will be either black or white depending on
background]) are in the middle of the graph, while the primary
producers (class 1, green), which do not consume members of any other
compartments, are at the other extreme. If we move through the graph
using the animation utility in Mage, the red class (class=4) contains
top predators such as Puerto Rican screech owls, Puerto Rican lizard
cuckoos, hawks (red-tailed, broad-winged, and sharp-shinned), Puerto
Rican boa snakes, colubrid snakes, ringed lizards, various predatory
snails, parasitic insects, and house cats. The basal/intermediate
consumers are divided into two primary classes. The first of these, the
black class (class=2) contains specialist herbivores and detritivores
such as decomposers (fungi and bacteria), various insects [ants and
bees (Hymenoptera), bark and book lice (Psocoptera), beetles
(Coleoptera),
bugs (Hemiptera), butterflies and moths (Lepidoptera), cockroaches,
mantids,
and walking sticks (Orthoptera), earwigs (Dermaptera), flies (Diptera),
Homopterans (cicadas), springtails (Collembola), termites (Isoptera),
thrips
(Thysanptera), and webspinners (Embioptera)], pseudoscorpions,
whip-scorpions,
sowbugs, pillbugs, bristletails, daddy longlegs, various snails, snakes
and
toads, various bats, various birds (Antillian euphonia, Puerto Rican
parrots,
ruddy quail-doves, striped-headed tanagers, bananaquits, Puerto Rican
bullfinches, ovenbirds, pigeons, thrushes, warblers, and woodpeckers),
and some mammals (black rats, Indian mongoose). The second isotrophic
class colored blue (class=3) contains primarily generalist omnivores
such as various insects (ants, flies, and orthopterans), spiders, mites
and ticks (Arachnids),
scorpions, centipedes, nematodes, various tree frogs, anole lizards (Anolis
sp.), and birds (prairie and black-throated blue warblers, black-cowled
orioles, Puerto Rican emeralds, green mangoes, Puerto Rican todies). It
is important to note the differences in the density (or linkage density
in ecology) of within class connections between the two isotrophic
classes. The blue class, in which members are omnivorous, have higher
within-class density than the black/white class and also exhibits loops
and cycles. The green class (class=1) contains the primary producers
and detritus such as plants, algae, live wood, sap, nectar, pollen,
dead wood, leaves, and detritus (with some exceptions discussed below).
Of interest are the two remaining isolated classes and some other notable anomalies. The maroon class (class=5) contains ostrocods and slime molds. Although they appear to play roles as top predators in the food web, by all accounts slime mold, for example, has rarely been conceived of as a top predator in ecology. In addition, the members of the orange class (class=6), which are both warblers, appear to function more as primary producers rather than in their true role as intermediate consumers. Finally, there is a small cluster of insects found among the plants and detritus in the green class (e.g., beetles, dragonflies, caddisflies, mayflies, vespids). Is the model not performing well, or is there some other explanation for these anomalous classifications? In reality the fault lies not with the model, but with the input data itself. The original food web matrix of trophic interactions contains incomplete data (e.g., we know warblers and mayflies must eat something -- they're not photosynthetic). Thus, the model places species into classes according to the nature of their trophic linkages as reported in the input data matrix.
One interesting outcome with respect to the discovery of these anomalies is the usefulness of an exploratory visualization tool such as Mage. Exploratory visualization programs such as Mage allow for an in-depth exploratory examination of the modeled data that facilitates both an interpretation of the model results and a cursory assessment of how well the model actually performed. Freeman (2000) discusses some of these issues in more depth in the first issue of the Journal of Social Structure.
The Coachella Valley Desert Food Web
We now turn to a more complex example of a food web. Although simpler with regards to the total number of compartments in the network, it is more complex in that the food web contains a high degree of cycles (A eats B, B eats C and C eats A), loops (A eats B and B eats A) and self loops (cannibalism). Polis (1995) provides a set of highly aggregated data for the Coachella Valley desert in California as an example of the importance and frequency of cycles and loops in understanding true food web dynamics, something he feels has been overlooked in most food web research. The matrix contains 30 compartments in which thousands of species were lumped together to produce compartments representing “kinds of organisms” and it is not clear how these aggregations were done. As with rain forest example, the problems with aggregation are possibly even more acute here.
These problems notwithstanding, we analyzed the Coachella Valley dataset using the methods presented earlier. Figure 9 shows the web with isotrophic classes indicated by color.
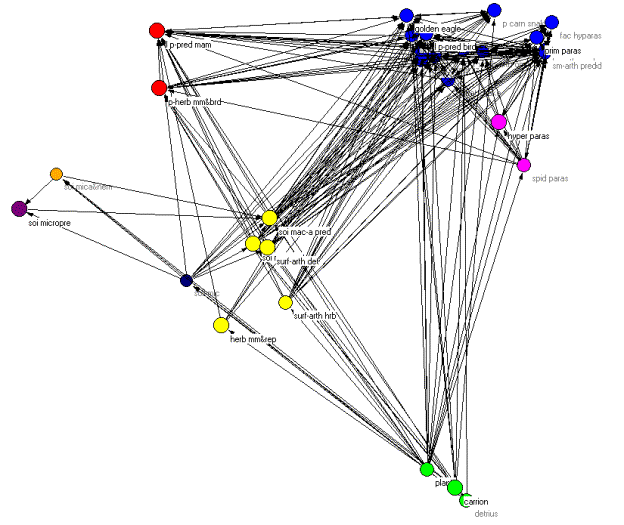
Figure 9. Pajek diagram of the regular role coloration of the Coachella Valley desert food web.
Figure 10 gives an interactive kinemage representation of
the same web.
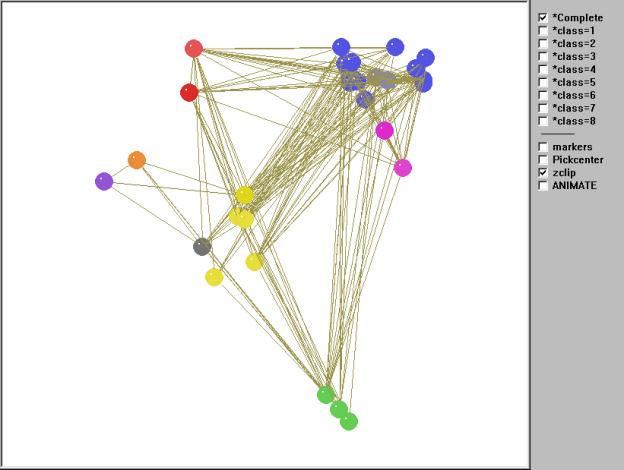
Figure 10. Kinemage of the regular role coloration of the Coachella Valley desert food web.
To animate Mage, click in the figure (may take a few seconds to load).
Once again we can orient the kinemage in trophic terms with primary producers (green class) at the bottom and animate through the various classes. However, unlike the other two examples, there are no clear top predators due to the high degree of cycles, loops, and self loops found in the food web. As Polis notes, "…the Coachella Valley ecosystem represents a community and food web with potentially no top predators" (535). This is precisely what the regular role coloration found. In fact, 66 percent of the compartments involves cannibalism and, as we shall see, one of the isotrophic groups contains trophic generalists with a high degree of cycles and loops. The primary producers (green class=1) contain the highly aggregated compartments plants, carrion, and detritus. The basal and intermediate consumers are found in four distinct isotrophic classes (classes 2, 6, 7, 8). The first of these, and the largest, contains primarily herbivorous specialists such as herbivorous mammals and reptiles, surface arthropod herbivores and detritivores, soil macroarthropods, and soil macroarthropod predators (yellow, class 2). The remaining three classes are all found in the soil and include soil microbes (black/white, class 6), soil microarthropods and nematodes (orange, class 7) and soil micro predators (purple, class 8).
Finally, there are three isotrophic classes making up the highest level in the food web. These include large, primarily predaceous mammals and primarily herbivores mammals and birds (red, class 3), hyperparasitoids and spider parasitoids (magenta, class 5), and a larger class containing golden eagles, large, primarily predaceous birds, various carnivorous snakes, birds and mammals, and various species of parasitoids (blue, class 4). Isotrophic class 4 constitutes what Polis (1995) refers to as carnivorous generalists as well as trophic generalists and also displays a high degree of looping and cycling. Hence, there are no clear top predators found in this community food web, something Polis (1995) notes may be more prevalent than catalogued food webs would have us believe.
Figure 11 summarizes the discussion above with an image graph, clarifying the overall structure.
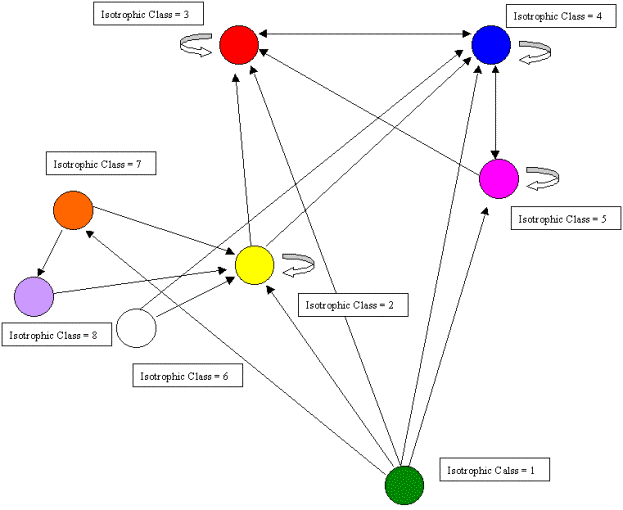
Figure 11. An image graph of the Coachella Valley food web showing cycles and loops.
Summary
This paper responds to the call by Yodzis and Winemiller (1999:339) “to further evaluate objective criteria for aggregation into trophospecies.” We have proposed that regular coloration models provide objective and formalized means for aggregating species into “isotrophic” classes that play similar structural roles in a network of trophic interactions. These isotrophic classes are a close match to the ecological notion of trophospecies.
Regular coloration models provide a rigorous way to describe the structure of food webs and formalize familiar notions such as trophic group, trophic equivalence, trophic position, complexity, niche, and niche overlap without necessarily losing too much information. Such models identify isotrophic species that face analogous environments, have similar functional roles, and are equally positioned in terms of trophic position, yet the regular coloration model does not presuppose a single linear trophic dimension nor does it forbid omnivory, cycles, loops, reflexive ties, cannibalism and other features of real food webs.
Basic regular coloration can be extended and adapted to examine special purpose problems in ecology. For example, to cluster species that exploit equivalent resources but do not necessarily have equivalent predators (such as a guild), it is possible to adjust the definitions to consider only outgoing (or incoming) ties (Pattison, 1988). Further, algorithms exist that relax the idealized mathematical definitions for application to noisy real world data of all kinds, including binary relations and quantitative energy flows. These models have the ability to handle multiple relations simultaneously and may facilitate the modeling of complex trophic and non-trophic interactions such as habitat facilitation and different types of competition.
References
Baird, D. and Ulanowicz, R. E. (1989). "The seasonal dynamics of the Chesapeake Bay ecosystem." Ecological Monographs 59: 329-364.
Baird, D. and Ulanowicz, R. E. (1993). "Comparative study on the trophic structure, cycling, and ecosystem properties of four tidal estuaries." Marine Ecology Progress Series 99: 221-237.
Baird, D., Luczkovich, J. J. and Christian, R. R. (1998). "Assessment of spatial and temporal variability in ecosystem attributes of the St. Marks National Wildlife Refuge, Apalachee Bay, Florida." Estuarine Coastal and Shelf Science 47: 329-329.
Batagalj, V., Doreian, P., and Ferligoj, A. (1992). "An optimization approach to regular equivalence." Social Networks 14: 121-135.
Batagelj, V. and Mrvar, A. (n.d.) Pajek. http://vlado.fmf.uni-lj.si/pub/networks/pajek/.
Borgatti, S. P., and Everett, M. G. (1993). "Two algorithms for computing regular equivalence." Social Networks 15: 361-376.
Borgatti, S. P., Everett, M. G., and Freeman, L. C. (1999). UCINET V. Software for Social Network Analysis. Natick: Analytic Technologies.
Boyd, J. P. (1969). "The algebra of group kinship." Journal of Mathematical Psychology 6: 139-167.
Burt, R. S., and Talmud, I. (1993). "Market niche." Social Networks 15: 133-149.
Christian, R. R. and Luczkovich, J. J. (1999). "Organizing and understanding a winter's seagrass foodweb network through effective trophic levels." Ecological Modelling 117: 99-124.
Christensen, V. and Pauly, D. (1992). A guide to ECOPATH II software system (Version 2.1). Manilla, Phillipines: ICLARM.
Christensen, V. and Pauly, D. (1993). Trophic Models of Aquatic Ecosystems. Manilla, Phillipines: ICLARM.
Cousins, S. H. (1987). "The decline of the trophic level concept." Trends in Ecology and Evolution 2: 312-316.
Cummins, K. W. (1974). "Structure and function of stream ecosystems." BioScience 24: 631-641.
Elton, C. S. (1927). Animal Ecology. London: Sidgwick and Jackson.
Everett, M. G. and Borgatti, S. P. (1991). "Role colouring a graph. Mathematical Social Sciences 21: 183-188.
Friedkin, N. E. and Johnson, E.C. (1990). "Social influences and opinions." Journal of Mathematical Sociology 15: 193-206.
Goldwasser, L. and Roughgarden, J. (1993). "Construction and analysis of a large Caribbean food web." Ecology 74: 1216-1233.
Goodenough, W.H. (1969). "Rethinking 'status' and 'role:' Toward a general model of the cultural organization of social relationships." Pages 311-330 in S. A. Tyler (ed.). Cognitive Anthropology. New York: Holt, Rinehart, and Winston. Nadel, S. F. (1957). The Theory of Social Structure. New York: Free Press.
Hawkins, C. P. and MacMahon, J. A. (1989). "Guilds: the multiple meanings of a concept." Annual Review of Entomology 34: 423-451.
Hirata, H. and Ulanowicz, R. E. (1985). "Information theoretical analysis of the aggregation and hierarchical structure of ecological networks." Journal of Theoretical Biology 116: 321-341.
Homans, G. C. (1961). Social Behavior: Its Elementary Forms. New York: Harcourt, Brace, and World.
Hubbell, C. H. (1965). "An input-output approach to clique identification." Sociometry 28: 377-399.
Jaccard, P. (1900). "Contribution au problame de l’immigration post-glaciaire de la flore alpine." Bull. Soc. Vandoise Sci. Nat. 36: 87-130
Kay, J. J., Graham, L. A. and Ulanowicz, R. E. (1989). "A detailed guide to network analysis." Pages 15-61 in F. Wulff, J. G. Field, and K. H. Mann. Network Analysis in Marine Ecology: Methods and Applications. Berlin: Springer-Verlag (284 pp.).
Katz, L. (1953). "A new index derived from sociometric data analysis." Psychometrika 18: 39-43.
Levine, S. (1980). "Several measures of trophic structure applicable to complex food webs." Journal of Theoretical Biology 83: 195-207.
Lorraine, F. and White, H. C. (1971). "Structural equivalence of individuals in social networks." Journal of Mathematical Sociology 1: 49-80.
Mayhew, B. (1980). "Structuralism vs. individualism, Part 1: Shadow boxing in the dark." Social Forces 59: 335-375.
Merton , R. K. (1957) Social Theory and Social Structure. New York: Free Press.
Monaco, M. E. and Ulanowicz, R. E. (1997). "Comparative ecosystem trophic structure of three U.S. Mid-Atlantic estuaries." Marine Ecology Progress Series 161: 239-254.
Paine, R. T. (1966). "Food web complexity and species diversity." The American Naturalist 100, No. 910: 65-75.
Patten, B. C. (1978). "Systems approach to the concept of environment." Ohio Journal of Science 78: 206-222.
Pattison, P. E. (1988). "Network models: Some comments on papers in this special issue." Social Networks 10: 383-411.
Perrson, L., Bengtsson, J., Menge, B. A. and Power, M. E. (1996). "Productivity and consumer regulation: Concepts, patterns, and mechanisms." In G. Polis and K. O. Winemiller. Food Webs: Integration of Patterns and Dynamics. New York: Chapman and Hall.
Pimm, S. L., Lawton, J. H., and Cohen, J. E. (1991). "Food web patterns and their consequences." Nature 350: 669-674.
Polis, G. A. (1991). "Complex trophic interactions in deserts: an empirical critique of food-web theory." American Naturalist 138: 123-155.
Polis, G. A. (1995). "Complex food webs." In B. C. Patten and S. E. Jorgensen. Complex Ecology: The Part-Whole Relations in Ecosystems. Englewood Cliffs, NJ: Prentice Hall PTR.
Reagan, D. P. and Waide, R. B. (1996). The Food Web of a Tropical Rain Forest. Chicago: The University of Chicago Press (616 pp.).
Richardson, D. C. and Richardson, J. S. (1992). "The kinemage: A tool for scientific communication." Protein Science 1, 3-9. http://kinemage.biochem.duke.edu/.
Root, R. B. (1967). "The niche exploitation pattern of the blue-gray gnatcatcher." Ecological Monographs 37: 317-350.
Simberloff, D. and Dayan, T. (1991). "The guild concept and the structure of ecological communities." Annual Review of Ecology and Systematics 22: 115-143.
Ulanowicz, R. E. (1986). Growth and Development: Ecosystems Phenomenology. New York: Springer-Verlag.
Ulanowicz, R. E. (1987). NETWRK4: A Package of Computer Algorithms to Analyze Ecological Flow Networks. Solomons, MD: University of Maryland, Chesapeake Biological Laboratory. http://www.cbl.cees.edu/~ulan/ntwk/network.html.
Ulanowicz, R. E. (1997). Ecology: The Ascendant Perspective. New York: Columbia University Press (201 pp.).
Wasserman, S. and Faust, K. (1995). Social Network Analysis: Methods and Applications. New York: Cambridge University Press.
White, D. R. and Reitz, K. P. (1985). Measuring Role Distance: Structural, regular and relational equivalence. Unpublished manuscript, University of California, Irvine.
White, H. C. (1963). An Anatomy of Kinship. Englewood Cliffs, NJ: Prentice Hall.
Yodzis, P. (1988). "The indeterminacy of ecological interactions as perceived through perturbation experiments." Ecology 69: 508-515.
Yodzis, P. (1989). Introduction to Theoretical Ecology. New York: Harper and Row.
Yodzis, P. and Winemiller, K. O. (1999). "In search of operational trophospecies in a tropical aquatic food web." Oikos 87: 327-340.
[1] Thanks to Roberta Chase for entering the rainforest data, and to Bob Ulanowicz and anonymous reviewers for helpful comments. This work was supported in part by the National Science Foundation under the Biocomplexity initiative grant SES 0083508.
[2] We use “food web” to refer to a network in which the nodes are species and an arc from A to B indicates that species A eats species B. In applications where energy flows are measured instead of eating behavior, the arcs point the other way.
[3] In addition, Burt and Talmud (1993) have noted that structural equivalence provides a nice way to define the concept of niche, although their focus was on market rather than ecological niches.
[4] In fact, a lattice (Borgatti, 1988; Borgatti and Everett, 1989).
[5] Note that the converse (that identically positioned nodes are regularly equivalent) is not true.
[6] It should be noted, however, that the regular coloration model does not in itself provide a quantitative measure of trophic level, such as provided by the method of Levine (1980). An extension of this kind seems feasible but is outside the scope of this paper.