JoSS Article: Volume 11

Bi-Annual Ratings of State Higher Education Systems 2000-2006

Fabio Guillermo Rojas^a and Amia Foston^b,

^a Assistant Professor at Indiana University,

^b Graduate Student at Indiana University

A Graph that Visualizes Social Science Sequence Data

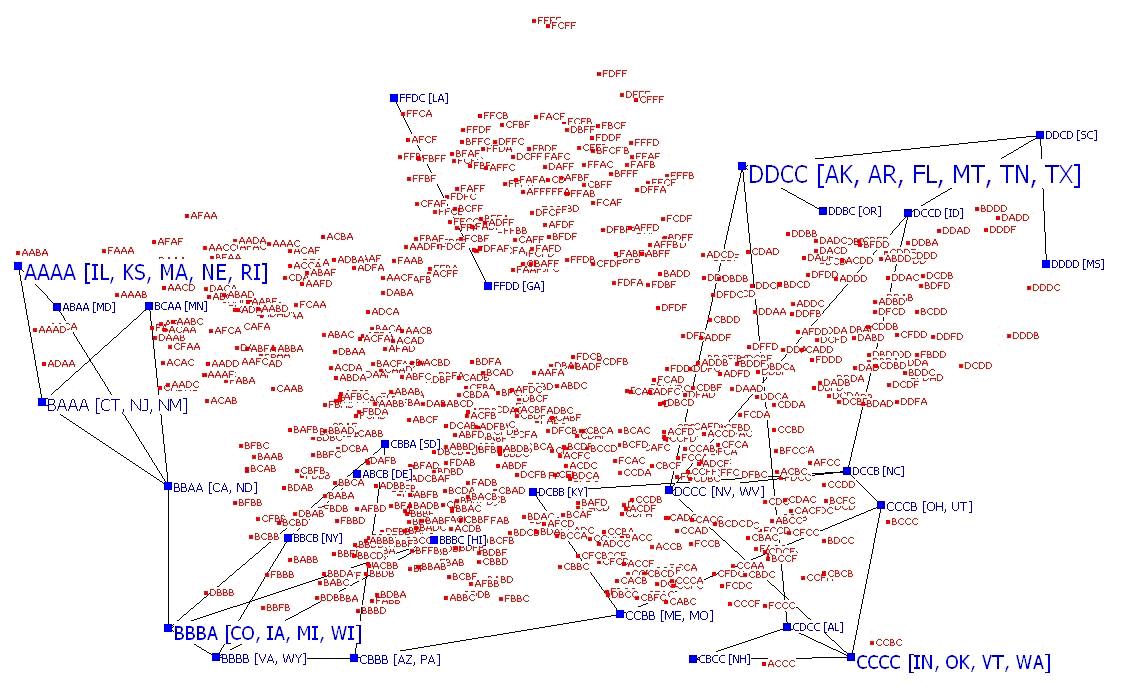
Self-Commentary

Two sequences (e.g., aabcb and abcaa) may be compared using a distance measure. The optimal matching algorithm computes the total number of substitutions and insertions (or deletions) required to transform one sequence to another (Abbott and Hrycak 1990). The optimal matching algorithm may be used to compute the adjacency matrix of any collection of sequences. In this diagram, two sequences are adjacent if their optimal matching distance is equal to one. Other distances may be used in different applications. Therefore, one may visualize the entire space of sequences of length T that employ N symbols using a graph based on the optimal matching algorithm. In creating a two dimensional representation of the graph, sequences that use only the Kth symbol are placed at the coordinates (sin (K2π/N), cos(K2π/N)). Thus, the “pure” sequences (e.g., aaaaa) are at the corners of a “star” with N corners. Other sequences are placed according to their most common symbol (e.g., a is the most common symbol of aaabb). If f is the frequency of the most common symbol in a sequence, the coordinates are f/T x (sin (K2π/N), cos(K2π/N)). The coordinates are randomly perturbed to prevent excessive node overlap. Informally, the homogeneous (“pure”) sequences are placed at the end points of a star with N points, others are placed on the interior, but close to the “pure” sequence with whom they share the most common symbol (e.g., aaabb and aaaaa are close to each other).

Graph visualization may guide analysis of observed sequences. Contrasting the sub-graph of observed sequences and the graph of all possible sequences can provide additional insight into the types of trajectories that may occur within the sample. We illustrate this idea with data from the National Center for Public Policy and Higher Education. This group issues its bi-annual report, Measuring Up: The National Report Card on Higher Education, that rates higher education systems in all fifty American states on the following five key performance indicators: preparation, participation, affordability, completion and benefits. Dropping “+’” and “-” affixes, we represent each state by its four bi-annual grades (A,B,C,D,F) on participation (percentage of 18 – 24 year olds enrolled in college) from 2000 to 2006. The space of all possible rating sequences is depicted in red. The blue nodes depict sequences associated with particular states. We have only retained links between observed sequences. The visualization shows that most states have stable evaluations. Most cases are concentrated around AAAA, BBBA, CCCC, and DDCC. Subsequent analysis can then classify cases according to the distance of these “anchor” points. For example, Southern educational systems appear close the to the DDCC sequence. This suggests a common institutional pattern in that geographical region. Subsequent analysis can test that hypothesis.

References

Abbott, Andrew and Alexandra Hrycak. 1990. "Measuring Resemblance in Sequence Data: An

Optimal Matching Analysis of Musicians' Careers." American Journal of Sociology 96:144-185.

National Center for the Public Policy and Higher Education. 2006. "Measuring Up 2006: The National Report Card on Higher Education." National Center for the Public Policy and Higher Education, San Jose, CA.

PEER REVIEW COMMENT No. 1

This visualization explores the distribution of State Higher Education grades by comparing all possible grading sequences to the observed sequences. The contrast between the constructed sequences in red and the observed sequences in blue illustrate the restricted range in which grades are actually given out. Moreover, the observed sequences show strong regional clustering in grades ( perhaps mapping onto geographical variation on educational funding or institutional strength?). This sequence graph clearly shows the state space for the outcomes of interest; it isn’t as “clean” as one might like, since many of the sequences run over each other (and the resolution seems low), making it somewhat difficult to read.

PEER REVIEW COMMENT No. 2

This visualization lays out the full range of possible combinations of grades on a state report card of key performance indicators and shows that of the many possible sequences, the empirical distribution tends to be very concentrated. The use of color contrast nicely highlights the state trajectories that have been mapped in blue against a backdrop of the red solution space with the A/B trajectories predominately representing Northern states and the C/D trajectories predominately representing Southern States. Although the non-random nature of the empirical distribution is clearly represented by this visualization, it is hard to find an overall pattern, and one wonders if there might be a way to somehow sharpen this display to layer more information?

PEER REVIEW COMMENT No. 3

This network diagram makes great use transforming distance. It also arrays the actual data in a permutation space, giving us a great sense of how this data falls within the space of all possibilities. I wonder how this visual might look if the y-axis was sensitive to trajectory – what would it tell us we could distinguish states with consistently improving grades from those without?